Différentes négations : langues naturelles et logiques

Surtout lorsque l’on en fait l’étude dans son fonctionnement linguistique, la négation est plus complexe que certaines études logiques l’ont, jusqu’à présent, imaginé. Dans un premier temps, nous préciserons brièvement quelques notions logiques utiles pour la discussion (concept, instances, intension et compréhension, classe extensionnelle d’un concept…). Dans un second temps, nous considérerons un certain nombre d’énoncés qui posent clairement des problèmes sérieux à la compréhension de la négation, surtout lorsqu’elle est pensée à l’intérieur d’une logique purement extensionnelle où un concept est caractérisé par uniquement la classe extensionnelle de ses instances. Dans un troisième temps, en nous plaçant dans le cadre de la Logique de la Détermination des Objets (LDO), nous analyserons ces énoncés, en prenant en compte non seulement l’extension d’un concept mais également son intension et son essence. Cela nous conduira à une structuration quasi-topologique de l’extension d’un concept (avec des intérieurs, des extérieurs et des frontières internes et externes). Nous appliquerons cette structuration quasi-topologique à l’analyse des marqueurs linguistiques encore / déjà et des marqueurs négatifs pas encore / déjà plus. Notre présentation restera assez intuitive, les aspects techniques étant traités dans d’autres publications.

1. La négation dans la « logique classique »

La logique classique manipule la négation d’une proposition en considérant que c’est une opération qui opère sur des propositions, signifiant « ce n’est pas le cas que… » ou « il est faux que… » ; par exemple, la proposition Athéna n’est pas une entité mortelle signifie que « il est faux que Athéna soit une entité mortelle » ou « ce n’est pas le cas que Athéna est une entité mortelle ». Pour mieux cerner la nature logique de la négation, nous partirons de l’Arbre de Porphyre, puis nous rappellerons quelques éléments succincts de la logique de Port Royal, avant de reprendre l’analyse du « concept » donnée par G. Frege, qui est à la base du développement de la logique « classique » ou Logique du Premier Ordre (LPO). Le cadre, simplement esquissé, de la Logique de la Détermination des Objets (LDO), qui complexifie la LPO ; nous permettra d’analyser des énoncés avec négation qui posent de réels problèmes à une logique purement extensionnelle.

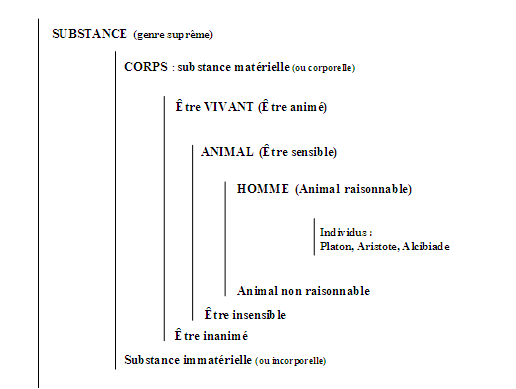
1.1. Division platonicienne : l’Arbre de Porphyre

Note de bas de page 1 :: Voir F. Chenique, Éléments de logique, 4 tomes, Paris, Dunod, 1975.

L’étude platonicienne de « l’être » introduit l’idée de division d’une idée plus générale en deux idées complémentaires. Par exemple, l’idée « substance » se divise en « substance matérielle ou corporelle » et « substance immatérielle ou non corporelle». Ce principe de la division platonicienne, avec des divisions en genres, espèces, différences spécifiques, propres, a été systématisé plusieurs siècles plus tard par les néoplatoniciens, en particulier par Porphyre1 (voir la figure 1). Une telle approche par division d’un concept doit être sérieusement complexifiée. Les réseaux sémantiques, que nous allons évoquer plus loin, sont l’une des voies de complexification mais, comme nous allons l’argumenter, elle reste encore insuffisante.

Figure 1 : Arbre de Porphyre (un extrait).

1.2. Logique de Port Royal

Note de bas de page 2 :: Antoine Arnauld et Pierre Nicole, La logique ou l’art de penser [1662], Paris, Gallimard, 1992 ; nous nous référons à l’édition de La logique ou l’art de penser [1662], Paris, Flammarion, 1970 (introduction Louis Marin) ; repris dans Gallimard, Paris, 1992. On peut se reporter aux excellents commentaires de Jean-Claude Pariente, L’analyse de langage à Port-Royal, six études logico-grammaticales, Paris, Minuit, 1985 et de Sylvain Auroux, La logique des idées, Paris, Vrin, 1993.

Dans leur ouvrage La logique ou l’art de penser 2, Antoine Arnauld et Pierre Nicole, considèrent que :

« La logique est l’art de bien conduire sa raison dans la connaissance des choses, tant pour s’instruire soi-même que pour en instruire les autres. (…) Cet art consiste dans les réflexions que les hommes ont faites sur les quatre principales opérations de leur esprit, concevoir, juger, raisonner et ordonner » (Logique, p. 30).

Les Messieurs de Port Royal partent des « idées » :

« Le mot d’idée est du nombre de ceux qui sont si clairs qu’on ne peut les expliquer par d’autres, parce qu’il n’y en a point de plus clairs et de plus simples ».

« Les idées qui ne représentent qu’une seule chose s’appellent singulières ou individuelles, et ce qu’elles représentent, des individus ; et celles qui représentent plusieurs s’appellent universelles, communes, générales ».
« L’idée d’animal convenant à tous les hommes convient aussi à tous les Éthiopiens »
« On joint quelquefois à un terme divers autres termes qui composent dans notre esprit une idée totale, de laquelle il arrive souvent qu’on peut affirmer ou nier ce qu’on ne pourrait pas affirmer ou nier de chacun de ces termes étant séparés ». (Logique, III, 5)

À chaque idée sont associées une « compréhension » et une « étendue » :

« Dans ces idées universelles, il y a deux choses qu’il est très important de bien distinguer, la compréhension et l’étendue.
J’appelle compréhension de l’idée, les attributs qu’elle enferme en soi, et qu’on ne peut lui ôter sans la détruire, comme la compréhension de l’idée de triangle enferme extension, figure, trois lignes, trois angles, et l’égalité de ces trois angles à deux droits, etc.
J’appelle étendue de l’idée les sujets à qui cette idée convient ; ce qu’on appelle aussi les inférieurs d’un terme général, qui, à leur égard, est appelé supérieur, comme l’idée de triangle en général s’étend à toutes les diverses espèces de triangle. » (Logique, I, 6)

La compréhension et l’étendue d’une idée entretiennent des rapports inverses, selon une « loi dite de Port Royal » (attribuée à Port Royal) :

« Plus la compréhension augmente, plus l’étendue diminue ; plus l’étendue augmente, plus la compréhension diminue ».

Cette loi signifie qu’une idée contient moins d’attributs qu’une des idées dominées par cette idée générale ; inversement, cette idée plus générale a une étendue plus vaste que l’une des idées particulières qu’elle domine. Par exemple, l’idée « animal » a une étendue qui contient l’étendue associée à l’idée « homme » (il y a moins d’êtres humains que d’animaux) mais la compréhension de l’idée « homme » a plus d’attributs que la compréhension de l’idée « animal ».

1.3. Le concept chez G. Frege

Note de bas de page 3 :: Voir Gottlob Frege, Grundgesetze der Arithmetik, begriffsschriftlich abgeleitet [1893], introduction, traduction et édition par Montgomery Furth, The Basic Laws of Arithmetic, exposition of the system, Berkeley, Los Angeles, University of California Press, 1967.

Dans son ouvrage Grungestze der Arithmetik (1893), Gottlob Frege3 considère deux types d’entités, d’un côté, les fonctions comme étant des entités « non saturées » et d’un autre côté, les objets comme étant des entités « saturées » :

« Je considère comme étant des objets chaque chose qui n’est pas une fonction, par exemple, des nombres, des valeurs de vérité et des “parcours-de-valeurs” (…) Les noms d’objets – les noms propres – dès lors n’impliquent aucune place d’argument ; ils sont saturés, comme les objets eux-mêmes » (§ 2, p. 36).

Un concept est ainsi, pour Frege, une fonction particulière qui associe à chaque élément d’un domaine une valeur de vérité, soit ‘le Vrai’, soit ‘le Faux’: la valeur de la fonction est ‘le Vrai’ lorsqu’un élément du domaine « tombe sous le concept », ou pour le dire autrement, lorsque le concept « s’applique à » cet élément, sinon c’est la valeur ‘le Faux’. Si le domaine ‘D’ est une classe d’objets individuels (par exemple Aristote, Platon, Alcibiade…), un concept d’individus ‘f’ (entité non saturée exprimée, par exemple, par « (…) est un habitant d’Athènes ») est une fonction de D dans {le Vrai, le Faux} : un individu quelconque ‘x’ de D « vérifie le concept ‘f’ » (ce que l’on peut encore exprimer par « ‘f’ est un attribut de ‘x’ ») lorsque la relation ‘f(x) = le Vrai’ est vraie, sinon c’est la relation ‘f(x) = le Faux’ qui est vraie. L’extension du concept ‘f’, notée ‘Ext [f]’, est un cas particulier du « parcours des valeurs de la fonction » (en fait le graphe de la fonction) ; elle est définie comme « l’ensemble de tous les individus qui vérifient le concept ‘f ‘ (ou qui tombent sous ‘f’) ; tous les individus de l’extension sont des instances du concept ‘f’. L’attribution d’un concept à un objet d’un domaine est le résultat d’un jugement qui considère que cet objet vérifie le concept et qu’il est ainsi une instance de ce concept.

« (…) par un jugement je comprends la reconnaissance de la vérité d’une pensée. La présentation dans l’idéographie (Begriffsschrift) d’un jugement par l’utilisation du signe “/-”, c’est ce que j’appelle une proposition de l’idéographie ou plus brièvement une proposition. Je considère ce “/-” comme étant composé de la ligne verticale, que j’appelle barre de jugement, et la ligne horizontale, que j’appellerai maintenant simplement horizontal. L’horizontal doit apparaître avec d’autres signes, comme ici la barre de jugement, et ne doit pas être confondu avec le signe moins. (…) Je considère ce signe comme un nom de fonction, comme suit : -Δ est le Vrai si Δ est le Vrai; c’est le Faux si Δ n’est pas le Vrai »(§ 5, p. 38).

La négation est également le résultat d’un jugement qui considère que, pour un objet donné, un concept n’est pas considéré comme l’un des attributs de cet objet, ce qui veut encore dire que cet objet ne tombe pas sous le concept. La logique « classique » ou Logique du Premier Ordre, héritée de G. Frege et B. Bussell, a souvent ramené l’étude d’un concept à sa seule extension selon le principe dit d’extensionalité : « deux concepts sont équivalents si et seulement si leurs extensions coïncident » ; autrement dit, deux concepts ne sont différenciés que par leurs extensions. Si l’on accepte, en plus, « la loi de Port Royal » établissant la dualité entre extension et intension, il n’apparaît plus nécessaire de tenir compte de l’intension puisque la seule connaissancede l’extension suffit à caractériser le concept. Aussi, pour beaucoup de logiciens (par exemple, R. Carnap, W.O. Quine…), l’intension étant ramenée à l’extension, il devient possible « d’oublier » l’intension et de se contenter de travailler avec les seules extensions. La négation d’un concept est alors complètement caractérisée par la partie complémentaire de l’extension de ce concept.

Remarque - Nous ne discuterons pas, dans cette publication, des différentes négations de la logique moderne. Dans le cadre de la « déduction naturelle » de Gentzen, on peut accepter la règle d’introduction de l’affirmation d’une proposition à partir de sa double négation – interprétée alors comme identique à l’affirmation, c’est-à-dire ‘non (non (p)) = p’ – mais on peut aussi refuser cette règle, conduisant alors, en particulier, à la « logique intuitionniste » qui n’accepte pas, entre autres, la validité du raisonnement par l’absurde suivant : si de l’hypothèse « non(p) », acceptée provisoirement, on en arrive, par des règles valides de déduction, à en déduire une contradiction (comme « (non (r)) & r » pour une certaine proposition ‘r’), alors la proposition « non (non (p)) » doit être considérée comme vraie. La logique « classique » accepte que la négation classique puisse satisfaire la loi de double négation, ce qui n’est pas le cas pour la négation intuitionniste.

Si extension et concept sont étroitement associés dans une logique extensionnelle, Frege reconnaît toutefois :

Note de bas de page 4 :: Gottlob Frege, Die Grundlagen der Arithmetik, (1884) note du § 69 ; traduction en français par C. Imbert, Les fondements de l’arithmétique, Paris, Seuil, 1969.
Note de bas de page 5 :: « Kritishche Beleuchtung einiger Punkte in E. Schröders Vorlesungen ûber dieAlgebra der Logik » (p. 455), cité dans l’introduction de Montgomery Furth (p. xl) à Gottlob Frege, The Basic Laws of Arithmetic, Berkeley and Los Angeles, University of California Press, 1967 [ traduction en anglais de Grungestze der Arithmetik (1893) ].

« (…) qu’on pourrait dire tout simplement “concept” à la place de “extension du concept”. Mais on s’exposerait à une double objection :
1) Ce serait en contradiction avec ce que j’ai précédemment affirmé (…)
2) Des concepts peuvent avoir même extension sans coïncider.
Je pense qu’on peut lever ces deux objections, mais ceci nous entraînerait trop loin »4.

« (…) On peut peut-être avoir l’impression (…) que dans le conflit entre les logiciens extensionnels et intensionnels [Logiker des Umfangs und [die] des Inhalts], je me situe du côté des derniers. Je tiens en fait le concept pour logiquement antérieur à son extension, et je considère comme futile la tentative de baser l’extension d’un concept sous la forme d’une classe non pas sur le concept mais sur des choses individuelles. »5

Frege considère que le concept a une certaine « préséance logique » sur son extension, et de ce fait il faudrait réserver une certaine place à la « compréhension » (ou à son intension) : deux concepts peuvent être équivalents en extension (lorsqu’ils s’appliquent aux mêmes objets) mais ils peuvent être différents et avoir, éventuellement, des intensions légèrement ou complètement différentes. Par exemple, le concept « (…) est-le-carré-de-l’unité » n’a pas exactement la même signification que le concept « (…) est-un-nombre-qui-est-inférieur-de-1-à-un-nombre-dont-le-carré-est-égal-à-son-double », bien que ces deux concepts aient la même extension ; de même, les concepts « (…) est-le-double-de-l’unité » et « (…) est-un-nombre-premier-pair » ont une même extension mais ils ont des significations (donc des compréhensions) assez différentes. Il est de même assez clair que les deux concepts « (…) est- bipède-sans-plumes » et « (…) est-animal-doué-de-raison » ne doivent pas être considérés comme ayant une même signification : ils n’évoquent pas la même idée en revoyant à des conceptualisations sous-jacentes assez différentes.

1.4. Logique de la Détermination des Objets

Note de bas de page 6 :: Voir Jean-Pierre Desclés, “Categorization : Logical Approach of Cognitive Problem”, Journal of Cognitive Science 3 (2), 2002, pp. 85-137 ; Jean-Pierre Desclés et Anca Pascu, “Logic of Determination of Objects. The Meaning of Variable in Quantification”, International Journal on Artificial Intelligence Tools, vol. 15, N° 6, 2006, pp. 1041-1052 ; “Logic of Determination of Objects (LDO) : How to Articulate Extension with Intension and Objects with Concepts ”, Logica Universalis, vol. 5, Issue 1, Springer, 2011 ; Anca Pascu, Les objets dans la représentation des connaissances. Application aux processus de catégorisation en informatique et sciences humaines, Habilitation à Diriger des Recherches, Université de Paris Sorbonne, 2006 ; Jean-Pierre Desclés, Anca Pascu et Christophe Jouis, “The Logic of Typical and Atypical Instances (LTA)”, in Proceedings of Florida Artificial Intelligence Research Science, Florida Artificial Intelligence Society XXVI, 2013.
Note de bas de page 7 :: La LDO ne reprend pas les hypothèses des « degrés d’appartenance » de la logique floue de L. Zadeh, « Fuzzy Sets », Information and Control, vol. 8, 1965, pp. 338–353.

La Logique de la Détermination des Objets (LDO)6 reprend la notion de « concept » de Frege (c’est-à-dire : un concept est analysé comme une fonction mathématique d’un domaine dans l’ensemble des valeurs de vérité {le Vrai, le Faux }) ainsi que celle de « l’extension » d’un concept mais elle cherche surtout à articuler « l’intension » (proche de la compréhension de Port Royal) avec l’extension et « l’étendue » d’un concept, sans toutefois adopter la « loi de Port Royal » qui établit une certaine dualité entre extension et intension. En effet, dans l’analyse des objets empiriques (puis, plus généralement, des objets abstraits) qui tombent sous un concept, il apparaît que les objets sont en fait des « plus ou moins bons représentants » du concept puisqu’un objet est considéré comme un « bon représentant » d’un concept lorsqu’il possède tous les attributs du concept. Ainsi, un homme typique qui possède tous les attributs du concept « (…) est-homme », a nécessairement deux bras, deux jambes, deux yeux, deux bras, un cœur… ; ces propriétés sont des attributs de ce que nous appelons « l’intension » du concept « (…) est-homme » . Cependant, parmi les hommes, donc dans l’extension de « (…) est-homme », il existe certaines instances comme les unijambistes, ou les humains privés d’un bras ou d’un œil… Or, de telles instances doivent être également considérées comme des hommes à part entière, c’est-à-dire comme des instances atypiques de la classe extensionnelle des hommes et surtout pas comme des individus qui seraient exclus de l’extension, même à un faible degré, car cela reviendrait à affirmer que ces instances atypiques ne seraient plus « tout à fait » des hommes, ou des instances à un degré moindre7. Ces instances atypiques n’héritent pas de certains des attributs de l’intension, qui caractérisent, par ailleurs, toutes les instances typiques ; cependant, pour être considérés comme des hommes à part entière, les instances atypiques doivent hériter des propriétés les plus essentielles qui caractérisent le concept « (…) est-homme », ces propriétés étant les constituants de « l’essence » du concept. Pour caractériser un concept, il faut donc définir non seulement son extension et son intension mais, également, son essence qui est contenue dans l’intension.

Note de bas de page 8 :: Eleonor Rösch, « Family Resemblance Studies in the Internal Structure of Categories », Cognitive Psychology 7, 1975, pp. 573-605 et « Human Categorization », in N. Warren (éd.) Advances in Cross Culture Psychology, vol.1, New York, Academic Press, 1977; Jean-Pierre Desclés, « L’implication entre concepts : la notion de typicalité », Travaux de Linguistique et de Littérature, XXIV, N° 1, 1986, pp. 179-102. ; Jean-François Le Ny, Science cognitive et compréhension du langage, Paris, PUF, 1989 et Comment l’esprit produit du sens, Paris, Odile Jacob, 2005 ; Danielle Dubois, Sémantique et cognition : catégories, prototypes, typicalité, Paris, Éditions du CNRS, 1991 ; Françoise Cordier et Jacques François, Catégorisation et langage, Paris, Hermès, Lavoisier, 2002.

L’extension d’un concept ne peut plus être pensée comme une simple classe d’instances toutes équivalentes entre elles, donc substituables les unes aux autres ; l’extension devient, dans le nouveau cadre de la LDO, un ensemble structuré où sont distinguées les instances typiques et les instances atypiques. Nous préciserons plus loin cette structuration de nature topologique. Dans l’étude de la catégorisation cognitive d’objets empiriques (et abstraits), la prise en compte de la typicalité et de l’atypicalité d’une instance (ou d’un exemplaire) d’un concept est devenue indispensable ; cela a été clairement mis en évidence par les psychologues (entre autres, Eleonor Rösch, et en France, Jean-François Le Ny, Françoise Cordier, Danielle Dubois …)8. Dans le cadre formel de la LDO, nous avons été conduits à structurer plus précisément l’intension et l’extension d’un concept et à ne pas définir la négation d’un concept comme renvoyant uniquement à la classe complémentaire de l’extension, comme nous allons le voir un peu plus loin avec quelques exemples problématiques lorsqu’on se restreint à interpréter les expressions négatives par une négation purement extensionnelle. Nous ne pouvons pas développer dans cet article les aspects techniques de la LDO, une logique non classique qui cherche à mieux articuler et penser les relations entre d’un côté, intension et essence d’un concept et, d’un autre côté, les objets extensionnels (plus ou moins déterminés) qu’ils soient typiques ou atypiques. Nous renvoyons aux publications déjà parues sur ce sujet.

Introduisons quelques notations : à chaque concept ‘f’, conçu comme une fonction d’un domaine dans l’ensemble {le Vrai, le Faux} des valeurs de vérité, sont associées son extension ‘Ext [f]’ et son intension ‘Int [f]’, c’est-à-dire des ensembles tels que :

Ext [f] =_def { x ∊ D ; f(x) = le Vrai }
Int [f] =_def { g ; f -> g } <=> (∀x) [ f(x) => g(x) ]

où la notation ‘->’ désigne « une relation de compréhension » entre le concept ‘f’ et l’un des attributs ‘g’ qu’il possède et fait ainsi partie de son intension. Nous ne supposons pas a priori la dualité entre extension et intension, puisque la prise en compte des instances atypiques la « détruit » ; ces instances atypiques n’héritent pas de tous les attributs de l’intension, tout en faisant pleinement partie de l’extension (et pas, insistons sur ce point, « à un degré moindre »). Dans le cadre de la LDO, nous distinguons donc, d’une part, la propriété fonctionnelle (ou conceptuelle) ‘f’, c’est-à-dire une fonction d’un domaine dans {le Vrai, le Faux} – ce que Frege appelle « concept » –, et d’autre part, le concept ‘^f’ qui doit alors être caractérisé par : 1°) la donnée de la propriété fonctionnelle ‘f’ ; 2°) une intension ‘Int[f]’, associée à ‘f’ ; 3°) une essence ‘Ess [f]’, également associée à ‘f’ et contenue dans l’intension. Un concept, désigné par ‘^f’ est maintenant caractérisé par < f, Int [f], Ess [f] >, avec toutes les conséquences que cela implique. Remarquons bien que, ainsi défini, le concept ‘^f’ ne coïncide pas avec ce que Frege a appelé « concept » (ce dernier étant identifié simplement à la propriété fonctionnelle ‘f’).

2. Quelques exemples problématiques de négations

La visée purement extensionnelle de la négation pose un certain nombre de problèmes logiques. Prenons, dans un premier temps, les deux énoncés suivants :

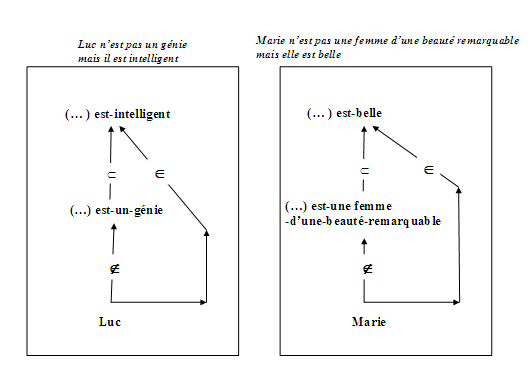
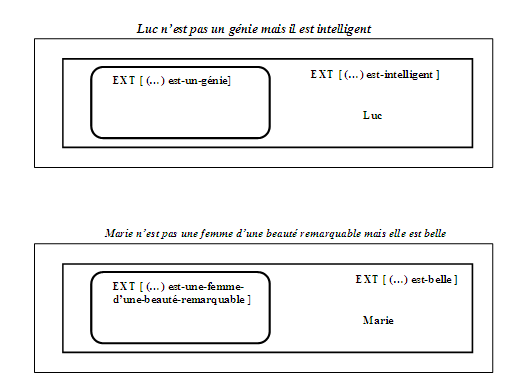
(1)	(a)	Luc n’est pas un génie mais il est intelligent.
	(b)	Marie n’est pas une femme d’une beauté remarquable mais elle est belle.

La négation présente dans ces deux énoncés ne pose aucun problème du point de vue extensionnel (et intensionnel). Il est, en effet, assez naturel d’admettre que Tout génie est également intelligent et que Toute femme qui est d’une beauté remarquable est également belle. Cela revient donc à considérer que certains attributs font partie des intensions des concepts respectifs, c’est-à-dire que l’on a les appartenances suivantes (le symbole ‘∊’ désigne la « relation d’appartenance » d’un objet à un ensemble) :

(2)	(a)	est-intelligent ∊ Int [ (…) est-un-génie ]
	(b)	(…) est-belle ∊ Int [ (…) est-une-femme-d’une-beauté-remarquable ]

ou, de façon équivalente, que les propositions, quantifiées universellement, sont vraies :

(3)	(a)	(x) [ (x) est-un-génie => (x) est-intelligent ]
	(b)	(x) [ (x) est-une-femme-d’une-beauté-remarquable => (x) est-belle ]

ce qui revient encore, du point de vue extensionnel, aux inclusions entre les classes extensionnelles :

(3)	(a)	Ext [(…) est-un-génie]  Ext [(…) est-intelligent]
	(b)	Ext [ (…) est-une-femme-d’une-beauté-remarquable]  Ext [ (…)est-belle]

Dire que Luc n’est pas un génie, c’est juger que « Luc », en tant qu’objet, n’appartient pas à l’extension du concept « (…) est-un-génie ». De la même façon, dire que Marie n’est pas d’une beauté remarquable, c’est juger que « Marie » n’appartient pas à l’extension du concept « (…) est-une-femme-d’une-beauté-remarquable », d’où les affirmations de non appartenance :

(4)	(a)	Luc  Ext[(…) est-un-génie]
	(b)	Marie  Ext[(…) est-une-femme-d’une-beauté-remarquable]

Ces négations de (4) signifient que « Luc » et « Marie » n’héritent pas des propriétés respectives « (…) est-un-génie » et « (…) est-d’une-beauté-remarquable » mais elles n’interdisent nullement que ces deux individus puissent, par ailleurs, appartenir aux extensions respectives Ext [(…) est-intelligent] et Ext [(…) est-belle] et donc hériter des propriétés constitutives de ces extensions. Accepter les énoncés de (1), c’est accepter le jugement : « les deux propositions de (5) sont vraies » :

(5)	(a)	(Luc) est-intelligent.
	(b)	(Marie) est-belle.

Figure 2 : Réseaux sémantiques et diagrammes extensionnels correspondants aux énoncés (1)

Note de bas de page 9 :: Jean-Pierre Desclés « Implication entre concepts : la notion de typicalité », 1986, et « Réseaux sémantiques : la nature logique et linguistique des relateurs », Travaux de Linguistique et de Littérature, op. cit., 1987 ; Jean-Pierre Desclés et Christine Froidevaux « Axiomatisation de la notion de repérage abstrait », Mathématiques et sciences humaines, N° 78, 1982, pp. 73-119.

Si nous représentons par des flèches la relation (d’appartenance ou de non appartenance) entre un objet individuel et le concept dont il est une instance ainsi que les relations (d’inclusion ou de subsomption) entre concepts, nous obtenons un « réseau sémantique »9. Nous représentons les énoncés de (1), sachant que l’on a admis les propositions universelles de (3) ou, de façon équivalente, les relations d’inclusions extensionnelles de (3’), représentées par des réseaux sémantiques auxquels nous pouvons associer des classes extensionnelles, d’où les visualisations figuratives de la figure 2.

Prenons maintenant une série d’autres énoncés pour lesquels l’analyse de la négation d’un seul point de vue purement extensionnel va poser quelques problèmes logiques. Considérons les énoncés parfaitement acceptables de (6), qui sont syntaxiquement (mais pas sémantiquement) assez proches de la forme des énoncés de (1) :

(6)	(a)	Luc n’est pas intelligent, c’est un génie !
	(b)	Marie n’est pas belle, c’est une femme d’une beauté remarquable !

Comme précédemment, continuons à admettre les propositions universelles précédentes de (3) et de (3’), qui expriment des relations entre unités lexicales. Dire que Luc n’est pas intelligent, cela signifie que « Luc » n’appartient pas à l’extension du concept « (…) est-intelligent » ; de même accepter Marie n’est pas belle c’est comprendre que « Marie » n’appartient pas à l’extension de « (…) est-belle ». En tenant compte des relations de (3) et de (3’), nous avons :

(7)	(a)	Luc  Ext [ (…) est-intelligent ] & Ext [(…) est-un génie ]  Ext [ (…) est-intelligent ]
	(b)	Marie  Ext [ (…) est-belle ] & Ext [(…) est-une-femme-d’une beauté-remarquable ]  Ext [ (…) est-belle]

A partir de ces deux propositions de (7), il devient impossible, du point de vue strictement extensionnel, d’en déduire (8) :

(7)	(a)	Luc ∊ Ext [ (…) est-un génie ]
	(b)	Marie ∊ Ext [ (…) est-une-femme-d’une beauté-remarquable ]

puisque si un élément quelconque (ici, « Luc » et respectivement « Marie ») n’appartient pas à une classe extensionnelle, il ne peut absolument pas appartenir à l’une de ses sous-classes strictes. Or, les énoncés de (6) expriment le contraire.

On peut citer d’autres exemples d’énoncés provoquant ce genre de difficultés logiques. A titre d’illustration, comparons les énoncés suivants :

(9)	(a)	Ce n’est pas un archevêque mais (simplement) un évêque.
	(b)	Médor n’est pas un chien mais seulement un mammifère qui aboie.
	(c)	Milou parle, certes, mais ce n’est tout de même pas un homme, c’est avant tout un animal qui nous paraît intelligent.

(9’)	(a)	Ce n’est pas un simple évêque mais c’est un archevêque !
	(b)	Attention ! Médor n’est pas un chien mais un caniche. Tout de même !
	(c)	Milou n’est pas un chien quelconque, c’est le chien de Tintin !

Si les énoncés de (9) ne posent aucun problème pour interpréter la négation dans un cadre purement extensionnel, en revanche, les énoncés de (9’) posent des problèmes analogues à ceux de (6). Les énoncés de (9) impliquent une « montée généralisante » dans un réseau de concepts, c’est-à-dire un passage d’un concept plus spécifique vers un concept plus général, alors que les énoncés de (9’) implique une « descente déterminative », c’est-à-dire un passage d’un concept vers une certaine spécification (soit vers une instance très particulière, soit vers un concept plus déterminé).

Doit-on en déduire que les langues sont des moyens d’expressions qui ne respecteraient pas la logique ? Doit-on en tirer la conclusion que la logique d’une part, et l’analyse sémantique des langues d’autre part, seraient, dans de nombreux cas, incompatibles et relèveraient de deux visées (rationnelles et sémiotiques) qui restent étrangères ?

3. Analyse dans le cadre de la Logique de la Détermination des Objets (LDO)

Nous considérons que la réponse aux deux questions précédentes est négative. L’histoire de la logique (au moins dans le monde occidental), depuis Aristote et les Stoïciens, a montré que la logique est profondément ancrée sur l’analyse sémantique des systèmes sémiotiques que sont les langues naturelles (ce qui ne veut pas dire qu’elle lui est entièrement réductible) : le grec ancien, puis le latin, et, ensuite, le français pour les logiciens de Port Royal ou l’allemand pour G. Frege, ou l’anglais pour B. Russell ou le polonais pour S. Lesniewski… ont été autant de supports sémiotiques qui ont contribué aux différentes conceptualisations entreprises pour élaborer une logique (une logique des propositions, des connecteurs entre propositions, une logique des opérations de prédication et de quantification, une logique des diverses modalités…).

Note de bas de page 10 :: Voir la note 4. La problématique de la LDO entretient certains rapports importants avec la logique paraconsistante développée par C. A. Da Costa Logiques classiques et non classiques – Essai sur les fondements de la logique, Paris : Masson, 1997 et par J.Y. Beziau, Handbook of Paraconsistency, London, King’s College, 2007. Signalons également les recherches entreprises sur la notion d’objet et son appréhension par Meinong de Brunot Leclerc « Quand c’est l’intension qui compte. Opacité référentielle et objectivité », Bulletin d’Analyse Phénoménologique, vol. 6, N° 8, 2010, pp. 83-108 et « En matière d’ontologie, l’important, ce ne sont pas les gains, mais la participation », Igitur, vol. 4, N° 2, avril 2012, pp. 1-24.

Les problèmes logiques révélés par l’interprétation des familles précédentes (1), (6), (9) et (9’) d’énoncés montrent qu’une logique purement extensionnelle, qui caractérise, rappelons-le, le concept par sa seule classe extensionnelle associée, ne peut rendre compte adéquatement de certains emplois de la négation. Des problèmes analogues surgissent lorsque l’on étudie les modalités autres que la négation. Pour répondre à ces problèmes, il faut réintroduire dans la logique formelle la vieille notion d’intension (et de compréhension de Port Royal). C’est ce qu’entreprend la LDO10 qui vise à élargir ainsi le cadre de l’analyse logique classique et des Langages du Premier Ordre.

Énoncer Luc n’est pas intelligent, c’est un génie, c’est vouloir affirmer plusieurs choses :

1°) « Luc » est un élément de l’extension du concept ‘(…) est-intelligent’, mais ce n’est pas un élément quelconque, ce qui revient à affirmer que :

« Luc »  Ext [ (…) est-intelligent ] - Ext [ (…) est-un-génie ] ;
(« Luc ») est-intelligent = le Vrai ;
« Luc » n’hérite pas nécessairement de tous les attributs de l’intension de ‘(…) est-intelligent’ ;

2°) « Luc » appartient à l’extension du concept ‘(…) est-un-génie’, d’où :

« Luc » ∊ Ext [ (…) est-un-génie ] ;
(« Luc ») est-un-génie ;
« Luc » hérite de tous les attributs du concept ‘(…) est-un-génie’.

Ce qui vient d’être affirmé prend sens puisque nous n’avons plus la propriété de « dualité extension-intension » (encore plus spécifique que la loi de Port Royal) selon laquelle une entité qui appartient à une classe extensionnelle associée à un concept hériterait de tous les attributs de l’intension de ce concept. Par conséquent, un élément peut donc appartenir à une sous-classe extensionnelle stricte de la classe extensionnelle d’un concept, sans nécessairement hériter de tous les attributs de l’intension de ce concept. Ainsi, l’élément « Luc » n’est pas un élément quelconque de la classe extensionnelle des entités intelligentes, puisqu’il appartient à la sous-classe extensionnelle des génies mais, tout en appartenant à la classe des entités intelligents, il n’hérite pas nécessairement de toutes les propriétés attribuées aux êtres intelligents, c’est-à-dire de toutes les propriétés de l’intension du concept ‘(…) est-intelligent’.

Si, maintenant, on distingue l’essence d’un concept de l’intension du même concept, (l’essence étant, rappelons-le, une partie de l’intension), l’individu « Luc » hérite alors nécessairement de toutes les propriétés de l’essence de ‘(…) est-intelligent’, et, « Luc » n’étant pas un élément quelconque de l’extension, il est catégorisé comme un élément distingué dans cette extension (puisqu’il est considéré comme un génie). Une instance d’un concept ‘(…) est-intelligent’ peut être une instance atypique (par exemple « Luc » peut ne pas savoir lire) dans l’extension de ce concept lorsqu’il se voit être attribué de propriétés qui peuvent être en contradiction avec certaines propriétés de l’intension de ce concept mais il hérite, par ailleurs, de toutes les propriétés de l’essence de ce concept. Ainsi, dans l’analyse de l’énoncé (6,a), on peut admettre que la propriété ‘(…) sait-lire’ est l’un des attributs du concept ‘(…) est-intelligent’ mais que cette propriété ne fait pas partie de son essence.

De ce qui précède, il découle que la négation est une opération dont l’analyse sémantique nous oblige à prendre en compte non seulement les extensions des concepts mais aussi les intensions, les essences et le refus de la simple « dualité extension-intension ». Nous pouvons donc maintenant considérer d’un côté, une négation purement extensionnelle (celle de la logique classique), cette opération faisant, en général, passer dans le complémentaire de l’extension d’un concept, la complémentarité étant établie par rapport à l’extension d’un concept plus général ; d’un autre côté, une négation non extensionnelle qui spécifie (ou détermine) une sous classe de l’extension d’un concept. La première négation « fait monter » dans un réseau sémantique de concepts ; la seconde négation « fait descendre », par détermination, d’un concept à un concept inférieur (plus déterminé) dans un réseau sémantique de concepts.

4. Réseau sémantique structuré par indentification, différenciation, rupture

Note de bas de page 11 :: Voir Antoine Culioli, Pour une linguistique de l’énonciation. Opérations et représentations, t. 1, Paris, Ophrys, 1990 et Variations sur la linguistique, Paris, Klincksieck, 2002 ; sur l’axiomatisation du repérage abstrait, voir Jean-Pierre Desclés et Christine Froidevaux, « Axiomatisation de la notion de repérage abstrait », op. cit., 1982 ; Jean-Pierre Desclés, « Réseaux sémantiques : la nature logique et linguistique des relateurs », op. cit., 1987.
Note de bas de page 12 :: Jean-PierreDesclés, Langages applicatifs, langues naturelles et cognition, Paris, Hermès, 1990, et « Une articulation entre syntaxe et sémantique cognitive : La grammaire applicative et cognitive », Mémoires de la Société de Linguistique de Paris, nouvelle série, Tome XX, Louvain, Peeters, 2011 ; Jean-Pierre Desclés et Zlatka Guentchéva, « Référentiels aspecto-temporels : une approche formelle et cognitive appliquée au français », Bulletin de la Société de Linguistique de Paris, N° 56 (1), 2011, pp. 95-127, et « Universals and Typology », in Binnick Robert (ed.) The Oxford Handbook of Tense and Aspect, Oxford University Press, 2012, pp.123-154.

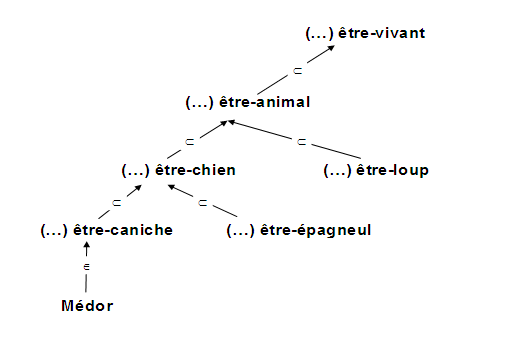
L’analyse des catégories grammaticales nous a conduits à définir la notion abstraite de repérage : repérage par identification (notée ‘=’) – relation réflexive, symétrique – ; repérage par différenciation (notée ‘’) – relation non symétrique – ; repérage par une mise en rupture (notée ‘#’) – relation irréflexive, symétrique et transitive11. Ces trois relations construisent un système de repérage qui peut se spécifier dans différentes catégories : la catégorie prototype des personnes où TU se différencie de JE et JE se différencie de TU et où IL est mis en rupture par rapport à JE et à TU ; le domaine spatial (relations entre lieux spatiaux comme ICI / LÀ-BAS // AILLEURS) ; le domaine temporel (relations entre instants et intervalles d’instants) ; le domaine spatio-temporel…12. Ces relations sont gérées par une axiomatisation à la base de différents référentiels (référentiel des personnes, référentiels temporels, référentiels spatiaux…) structurés de façon interne (par identification et différenciation) et articulés entre eux par la relation de mise en rupture. Dans le domaine des relations entre concepts associés à des lexèmes lexicaux, la notion de repérage est également opératoire : la relation d’identification (=) tient entre des concepts synonymes car sémantiquement « très proches », ayant « presque » la même intension ; la relations d’appartenance d’une instance à un concept et les relations d’inclusion (subsomption) entre concepts sont des relations particulières de différenciation () entre concepts qui ont en commun une même essence avec des propriétés caractéristiques qui les différencient entre eux ; la relation de mise en rupture (#) différencie des concepts jugés indépendants. La différenciation apparaît comme une négation faible tandis que la mise en rupture est visiblement une négation forte. Un réseau sémantique de concepts est ainsi structuré par ces trois relations de repérage. Nous en donnons un exemple dans la figure 3. Dans un tel réseau, deux concepts (ou une instance d’un concept) peuvent être dans une relation de différenciation (inclusion ou appartenance). On peut complexifier le réseau en introduisant des concepts synonymes – par exemple ‘(…) être chien’ et ‘(…) être cabot’) – ou en indiquant des mises en rupture entre concepts jugés entièrement hétérogènes. La négation opère à l’intérieur du réseau soit par une « montée généralisante », ce qui revient à nier certaines des propriétés caractérisantes d’un individu (Médor n’est pas un caniche mais (simplement) un chien) ; soit par une « descente déterminative » où l’on ajoute de propriétés plus caractérisantes (Médor n’est pas un (simple) chien mais un caniche / Un caniche n’est pas un (simple) chien !) ; soit encore par un changement radical de conceptualisation mettant en rupture deux concepts jugés hétérogènes (Médor n’est pas un chien mais un loup / Un chien n’est pas un loup). La logique classique a, semble-t-il, privilégié cette dernière négation.

Figure 3 : Un réseau sémantique.

5. Structuration quasi-topologique et négation

Note de bas de page 13 :: Sur la notion de quasi-topologie, qui étend la topologie en introduisant la frontière interne et la frontière externe d’un lieu, voir, entre autres, Jean-Pierre Desclés et Zlatka Guentchéva, « Quasi topological representations (QTR) of Spatial places and spatio-temporal movements in natural languages », in Z, Marotta Giovani et al. (éds.), Space in Language, Proceedings of the Pisa International Conference, 2010, pp. 213- 233, et « Trimorphe et topologie », inA. Ouattara (éd.), La linguistique de Bernard Pottier : bilan, critiques, perspectives, Reims, Presses Universitaires de Reims, 2011, pp. 218-252. La quasi-topologie trouve une pertinence non seulement en sémantique mais également en anthropologie.
Note de bas de page 14 :: Sur la notion de schème sémantico-cognitif (SSC), voir, entre autres, les références de la note 11. Par ailleurs, Bernard Pottier introduit également la notion de schème pour décrire la signification d’unités lexicales dans Représentations mentales et catégorisations linguistiques, Louvain-Paris, Peeters, 2000, et Images et modèles en Sémantique, Paris, Honoré Champion, 2012.

L’articulation entre intension et extension conduit à un espace muni d’une structure quasi-topologique (c’est-à-dire avec des frontières interne et externe)13 sur lequel la négation peut opérer. Considérons une unité verbale, comme ‘(…)est-arrivé’, dont la signification est décrite par un schème sémantico-cognitif14 spatio-temporel qui décrit un mouvement de l’extérieur d’un lieu vers la frontière de ce lieu. Prenons, par exemple, les énoncés suivants :

(10)	(a)	Luc n’est pas encore arrivé à l’aéroport.
	(b)	Luc est presque déjà arrivé à l’aéroport mais pas tout à fait.
	(c)	L’avion est vraiment arrivé à l’aéroport.
	(d)	L’avion n’est pas arrivé.

Les énoncés (10,a) et (10,b) sont des formes de négation de l’énoncé (10,c). Ces deux négations sont différentes de la négation radicale (10,d). Les énoncés (10,a) et (10,b) décrivent un mouvement spatio-temporel de l’entité « l’avion » et la localisent dans le voisinage du lieu « l’aéroport », alors que (10,c) décrit une position uniquement spatiale et pas une situation évolutive. Les positions successives exprimées par (10,a) et (10,b) ne sont cependant pas équivalentes : (10,a) indique un mouvement qui fait passer de l’extériorité du lieu « l’aéroport » dans une zone spatio-temporelle voisine de ce lieu visé ; les positions successives de « l’avion » sont déclarées, par (10,a), plus éloignées du lieu visé (« l’aéroport ») que les positions successives de « l’avion » dans la zone temporelle exprimée par (10,b).

Prenons maintenant les deux concepts ‘(…) est-jeune’ et ‘(…) est-vieux’. Ces deux concepts sont « voisins » car ils indiquent une orientation déterminée qui fait passer de l’état de jeunesse vers l’état de vieillesse mais pas l’inverse ; chacun de ces concepts admet des variations d’intensité (on est plus ou moins jeune ou plus ou moins vieux, on est très jeune ou très vieux…). Les extensions de ces deux concepts reçoivent une structuration temporelle quasi-topologique : une entité peut en effet passer par différentes positions localisées par rapport aux extensions, dans des zones précises qui correspondent à des propriétés plus spécifiques ; pour le concept ‘(…) est jeune’, on a les propriétés associées :

‘(…) est-vraiment-jeune’, ‘(…) est-encore-jeune’,
‘(…) n’est-déjà- plus-jeune’

On a également pour le concept ‘(…) est-vieux’, les propriétés associées :

‘(…) n’est-pas-encore-vieux’, ‘(…) est-déjà-vieux, ‘(…) est-vraiment-vieux’.

Note de bas de page 15 :: La notion de « trimorphe » introduite par B. Pottier est généralisée par le « trimorphe topologique » dans Jean-Pierre Desclés et Zlatka Guentchéva, « Trimorphe et topologie », op. cit. 2011.

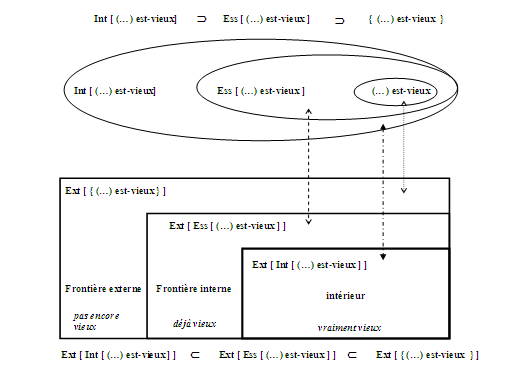
Les différentes parties extensionnelles sont des parties quasi-topologiques de l’extension des concepts correspondants. Plus précisément, pour le concept ‘(…) est-jeune’, « l’intérieur », respectivement « la frontière interne », « la frontière externe » de son extension ; pour le concept ‘(…) est-vieux’, « la frontière externe », respectivement « la frontière interne » et « l’intérieur » de son extension. Ces différentes parties quasi-topologiques (intérieurs, frontières, extérieurs)15 sont mises en correspondance avec l’intension, l’essence et la simple propriété associées à un concept (voir la figure 4).

Figure : 4 : Correspondance entre les extensions topologiques et les intensions, essences et propriété.

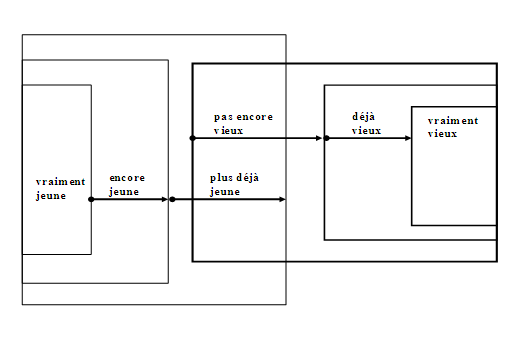
Les deux concepts étant voisins, certaines parties extensionnelles peuvent éventuellement se recouvrir. En effet, on peut parfois considérer que la zone extensionnelle correspondante à la propriété plus spécifique « (…) n’est-déjà-plus jeune » peut recouvrir en partie la zone extensionnelle correspondante à la propriété plus spécifique « (…) n’est-pas-encore-vieux », comme dans l’énoncé Certes, il n’est déjà plus jeune mais on peut considérer qu’il n’est pas encore vieux. La négation peut opérer évidement en faisant passer d’un concept à un autre, mais elle peut également opérer à l’intérieur des parties quasi-topologiques d’une même extension, ou encore entre les frontières qui se recouvrent pour deux concepts voisins (voir figure 5), comme l’illustrent les énoncés de (11) :

(11)	(a)	Luc est vraiment jeune.
	(b)	Luc n’est plus un vrai jeune.
	(c)	Luc est encore jeune mais plus tout à fait vraiment jeune.
	(d)	Luc n’est déjà plus vraiment jeune.
	(e)	Luc n’est pas jeune, il est vieux.
	(f)	Luc n’est pas encore vieux et il n’est déjà plus jeune.
	(g)	Luc n’est pas déjà vieux mais il vieillit de plus en plus vite.
	(h)	Luc est presque vieux mais pas déjà un vrai vieux.
	(i)	Luc est vraiment vieux

Figure 5 : Chevauchement des frontières externes extensionnelles pour deux concepts voisins
‘(…) est-jeune’ et ‘(…) est-vieux’.

Les opérateurs aspectuels encore et déjà ont des négations associées pas encore et déjà plus ; ces quatre opérateurs déterminent des frontières internes et externes d’un lieu cognitif. On peut montrer qu’ils s’organisent dans un carré sémiotique, analogue au carré logique attribué à Aristote. Faute de place, nous ne pouvons pas développer ce carré sémiotique dans lequel négation et aspectualité entrent en interaction.

6. Conclusion

Il est clair que les analyses qui viennent d’être présentées demanderaient de plus amples développements techniques, tant du point de vue linguistique que du point de vue logique et mathématique. De plus, ces recherches, placées dans le cadre logique de la LDO, sont loin d’être achevées car elles sont en cours de développement, donc rectifiables ou complexifiables.

Note de bas de page 16 :: Voir une analyse détaillée dans Jean-Pierre Desclés, Anca Pascu et Christophe Jouis, « The Logic of Typical and Atypical Instances (LTA) », op. cit., 2013.

Comme nous l’avons vu dans cet exposé, la notion de négation peut opérer à l’intérieur d’un réseau sémantique structuré de concepts et indiquer des opérations assez différentes : soit une « montée par abstraction » dans le réseau, ce qui est compatible avec une visée purement extensionnelle des concepts ; soit par une « descente par détermination » dans le réseau, cette descente posant, elle, de sérieuses difficultés pour une visée seulement extensionnelle de la négation ; soit encore, par le signalement d’une erreur de conceptualisation, elle établit un changement (une mise en rupture) entre deux concepts hétérogènes. Dans l’approche défendue par la LDO, l’extension d’un concept n’est pas une simple classe d’équivalence où toutes les instances seraient substituables les unes aux autres car elle est structurée par les instances typiques et les instances atypiques. En tenant compte qu’un concept n’est pas seulement une simple propriété fonctionnelle (ou fonction d’un domaine dans {le Vrai, le Faux}) mais est caractérisé également par une intension et une essence, partie de l’intension, l’extension est munie d’une structure quasi-topologique avec d’un côté, « l’intérieur de l’extension », constitué de toutes les instances qui héritent de tous les attributs de l’intension, donc de toutes les instances typiques du concept et d’un autre côté, une extension plus vaste, constituant l’extension du concept, c’est-à-dire de toutes les instances qui héritent nécessairement des concepts de l’essence mais pas obligatoirement de tous les attributs de l’intension. Les instances atypiques sont donc des instances qui se trouvent localisées dans la différence qui tient entre l’extension globale du concept et l’extension, plus restreinte, comprenant uniquement les instances typiques. Comme le concept ‘^f = < f, Int(f), Ess(f) > doit être distingué de la propriété fonctionnelle ‘f’, l’extension du concept ‘Ext(^f)’ devient une partie de l’extension de la propriété fonctionnelle ‘Ext(f)’ qui est indépendante de la structuration apportée par la prise en compte de l’intension et de l’essence. La négation peut ainsi opérer à l’intérieur de l’extension du concept en affirmant par exemple qu’une instance n’est pas typique mais seulement atypique ou l’inverse ; elle peut aussi opérer en indiquant qu’un objet qui tombe sous la propriété fonctionnelle ‘f’ n’est pas pour autant une instance du concept ‘^f’, cet objet n’héritant plus alors de tous les attributs qui constitue l’essence du concept. À titre d’illustration, prenons le cas d’un « SDF » (individu sans domicile fixe) ; ce dernier tombe bien sous le concept ‘(…) être-un-habitant-d’une-cité’ sans pour autant hériter de l’attribut ‘(…) a-une-adresse-dans-la-cité’, qui est l’une des propriétés de l’essence du concept précédent16, ce qui permet de pouvoir affirmer que Un SDF est seulement un « habitant marginal » d’une cité mais il n’est pas un habitant de cette cité puisqu’il n’a pas de domicile dans cette cité (et encore moins un véritable habitant qui, lui, paye les taxes de la cité), la propriété ‘(…) paie-les-taxes-de-la-cité’ étant considérée comme une propriété de l’essence.

Note de bas de page 17 :: Les notions de « référentiel » et de « changement de référentiel » deviennent de plus en plus importantes dans l’analyse sémantique, ce qui permet d’unifier de nombreuses analyses. Voir, entre autres, Jean-Pierre Desclés et Zlatka Guentchéva, « Référentiels aspectotemporels : une approche formelle et cognitive appliqué au français », op. cit., 2011.

Terminons par une dernière remarque. L’analyse référentielle de la négation dans un énoncé comme Luc n’est pas arrivé, implique que l’on tienne compte de la notion de « référentiel » et surtout de « changement de référentiel »17 puisque, dans l’énoncé cité, il est indiqué que la situation exprimée par l’énoncé positif Luc est arrivé n’est pas actualisée dans le référentiel énonciatif de l’énonciateur, ce qui signifie que la situation positive « Luc est arrivé » fait partie d’un autre référentiel, c’est-à-dire du référentiel des situations non actualisées dans le référentiel énonciatif, ce dernier étant le référentiel des situations verbalisées par l’énonciateur comme étant déjà actualisées, ou en cours d’actualisation ou encore éventuellement actualisables ultérieurement. Pour nier une situation, l’énonciateur doit donc être capable de se représenter cette situation dans un autre référentiel et, ensuite, juger que cette situation n’est pas actualisée dans le référentiel énonciatif. C’est là une propriété remarquable de la négation : nier c’est être capable de se représenter la situation positive et juger qu’elle n’est pas actualisée ou n’a pas été actualisée ou ne peut pas être actualisée.

La négation, telle qu’elle est appréhendée et exprimée par les systèmes sémiotiques que sont les langues naturelles, nous apparaît comme loin d’être une opération simple, en tout cas beaucoup moins simple que l’opération de négation qui a été jusqu’à présent captée par une logique purement extensionnelle. Cela ne veut toutefois pas dire que la logique doit se désintéresser de la complexité de la négation, au besoin en se complexifiant elle-même et en étendant le domaine empirique de ses recherches.

Bibliographie

Arnauld Antoine, Nicole, Pierre, La logique ou l’art de penser [1662], introduction Louis Marin, Paris, Gallimard, 1992.

Auroux Sylvain., La logique des idées, Paris, Vrin, 1993.

Beziau Jean-Yves, Carnielli, W. et Gabbay, D. (éds.), Handbook of Paraconsistency, London, King’s College, 2007.

Chenique François., Éléments de logique, 4 tomes, Paris, Dunod, 1975.

Cordier Françoise, François Jacques, Catégorisation et langage, Paris, Hermès, Lavoisier, 2002.

Culioli Antoine, Pour une linguistique de l’énonciation. Opérations et représentations, t. 1, Paris, Ophrys, 1990.

– Variations sur la linguistique, Paris, Klincksieck, 2002.

Da Costa, C. A. (éd.), Logiques classiques et non classiques – Essai sur les fondements de la logique, Paris, Masson, 1997.

Descles, Jean-Pierre, « L’implication entre concepts : la notion de typicalité », Travaux de Linguistique et de Littérature, XXIV, N° 1, 1986, pp. 179-102.

– « Réseaux sémantiques : la nature logique et linguistique des relateurs », Langages, N° 87, 1987, pp. 57-78.

– Langages applicatifs, langues naturelles et cognition, Paris, Hermès, 1990.

– « Categorization : Logical Approach of Cognitive Problem », Journal of Cognitive Science 3 (2), 2002, pp. 85–137.

– « Une articulation entre syntaxe et sémantique cognitive : La grammaire applicative et cognitive », Mémoires de la Société de Linguistique de Paris, nouvelle série, Tome XX, L’architecture des théories, les modules et leurs interfaces, Louvain, Peeters, 2011, pp. 115-153.

DesclesJean-Pierre, Froidevaux Christine, « Axiomatisation de la notion de repérage abstrait », Mathématiques et sciences humaines, N° 78, 1982, pp. 73-119.

DesclesJean-Pierre, Guentcheva Zlatka, « Quasi topological representations (QTR) of Spatial places and spatio-temporal movements in natural languages », in Z, Marotta Giovani et al. (éds.), Space in Language, Proceedings of the Pisa International Conference, 2010, pp. 213- 233.

– « Référentiels aspectotemporels: une approche formelle et cognitive appliqué au français » in Bulletin de la Société de Linguistique de Paris, 2011, N° 56 (1), 2011, pp. 95-127.

– « Trimorphe et topologie », in A. Ouattara (ed.), La linguistique de Bernard Pottier : bilan, critiques, perspectives, Reims, Presses Universitaires de Reims, 2011, pp. 218-252.

–« Universals and Typology », in Binnick R. (ed.) The Oxford Handbook of Tense and Aspect, Oxford University Press, 2012, pp. 123-154.

DesclesJean-Pierre, Pascu, Anca, « Logic of Determination of Objects. The Meaning of Variables in Quantification », International Journal on ArtificialIntelligence Tools, vol. 15, N° 6, 2006, pp. 1041-1052.

– « Logic of Determination of Objects (LDO) : How to Articulate “Extension” with “Intension” and “Objects” with “Concepts” », Logica Universalis, vol. 5, Issue 1, Springer, 2011, pp. 75.

DesclesJean-Pierre, PascuAnca,, JouisChristophe,, « The Logic of Typical and Atypical Instances (LTA) », inProceedings of Florida Artificial Intelligence Research Science, FLAIRS XXVI, Florida, 2013.

Dubois, Danielle, Sémantique et cognition : catégories, prototypes, typicalité, Paris, Éditions du CNRS, 1991.

Frege Gottlob, Die Grundlagen des Arithmetik, Verlag von Wilhem Koebner, Breslau, 1884; traduction française de Claude Imbert, Les fondements de l’arithmétique, Paris, Editions du Seuil, 1969.

– Grundgesetze der Arithmetik, begriffsschriftlich abgeleitet (1893), translated and edited, with an introduction, by Montgomery Furth: The Basic Laws of Arithmetic, exposition of the system, Berkeley and Los Angeles, University of California Press, 1967.

LeclercqBrunot, « Quand c’est l’intension qui compte. Opacité référentielle et objectivité », in Bulletin d’Analyse Phénoménologique, vol. 6, N° 8, 2010, pp. 83-108.

– « En matière d’ontologie, l’important, ce ne sont pas les gains, mais la participation», Igitur, vol4, N° 2, avril 2012, pp. 1-24.

Le Ny Jean-François., Science cognitive et compréhension du langage, Paris, PUF, 1989.

– Comment l’esprit produit du sens, Paris, Odile Jacob, 2005.

Pariente J.C., L’analyse de langage à Port -Royal, six études logico-grammaticales, Paris, Les Éditions de Minuit, 1985.

Pascu Anca, Les objets dans la représentation des connaissances. Application aux processus de catégorisation en informatiqueet sciences humaines, Habilitation à Diriger des Recherches, Université de Paris Sorbonne, 2006.

Pottier Bernard, Représentations mentales et catégorisations linguistiques, Louvain-Paris, Peeters, 2000.

– Images et modèles en Sémantique, Paris, Honoré Champion, 2012.

RöshEleonor, Mervis, C. B., « Family Resemblance Studies in the Internal Structure of Categories », Cognitive Psychology 7, 1975, pp. 573-605.

RöshEleonor, « Human Categorization », in N. Warren (ed.) Advances in Cross Culture Psychology, vol.1, New York, Academic Press, 1977.

Zadeh L. A. (éd.), « Fuzzy Sets », Information and Control, vol. 8, 1965, pp. 338–353.

Notes

1 Voir F. Chenique, Éléments de logique, 4 tomes, Paris, Dunod, 1975.

2 Antoine Arnauld et Pierre Nicole, La logique ou l’art de penser [1662], Paris, Gallimard, 1992 ; nous nous référons à l’édition de La logique ou l’art de penser [1662], Paris, Flammarion, 1970 (introduction Louis Marin) ; repris dans Gallimard, Paris, 1992. On peut se reporter aux excellents commentaires de Jean-Claude Pariente, L’analyse de langage à Port-Royal, six études logico-grammaticales, Paris, Minuit, 1985 et de Sylvain Auroux, La logique des idées, Paris, Vrin, 1993.

3 Voir Gottlob Frege, Grundgesetze der Arithmetik, begriffsschriftlich abgeleitet [1893], introduction, traduction et édition par Montgomery Furth, The Basic Laws of Arithmetic, exposition of the system, Berkeley, Los Angeles, University of California Press, 1967.

4 Gottlob Frege, Die Grundlagen der Arithmetik, (1884) note du § 69 ; traduction en français par C. Imbert, Les fondements de l’arithmétique, Paris, Seuil, 1969.

5 « Kritishche Beleuchtung einiger Punkte in E. Schröders Vorlesungen ûber dieAlgebra der Logik » (p. 455), cité dans l’introduction de Montgomery Furth (p. xl) à Gottlob Frege, The Basic Laws of Arithmetic, Berkeley and Los Angeles, University of California Press, 1967 [ traduction en anglais de Grungestze der Arithmetik (1893) ].

6 Voir Jean-Pierre Desclés, “Categorization : Logical Approach of Cognitive Problem”, Journal of Cognitive Science 3 (2), 2002, pp. 85-137 ; Jean-Pierre Desclés et Anca Pascu, “Logic of Determination of Objects. The Meaning of Variable in Quantification”, International Journal on Artificial Intelligence Tools, vol. 15, N° 6, 2006, pp. 1041-1052 ; “Logic of Determination of Objects (LDO) : How to Articulate Extension with Intension and Objects with Concepts ”, Logica Universalis, vol. 5, Issue 1, Springer, 2011 ; Anca Pascu, Les objets dans la représentation des connaissances. Application aux processus de catégorisation en informatique et sciences humaines, Habilitation à Diriger des Recherches, Université de Paris Sorbonne, 2006 ; Jean-Pierre Desclés, Anca Pascu et Christophe Jouis, “The Logic of Typical and Atypical Instances (LTA)”, in Proceedings of Florida Artificial Intelligence Research Science, Florida Artificial Intelligence Society XXVI, 2013.

7 La LDO ne reprend pas les hypothèses des « degrés d’appartenance » de la logique floue de L. Zadeh, « Fuzzy Sets », Information and Control, vol. 8, 1965, pp. 338–353.

8 Eleonor Rösch, « Family Resemblance Studies in the Internal Structure of Categories », Cognitive Psychology 7, 1975, pp. 573-605 et « Human Categorization », in N. Warren (éd.) Advances in Cross Culture Psychology, vol.1, New York, Academic Press, 1977; Jean-Pierre Desclés, « L’implication entre concepts : la notion de typicalité », Travaux de Linguistique et de Littérature, XXIV, N° 1, 1986, pp. 179-102. ; Jean-François Le Ny, Science cognitive et compréhension du langage, Paris, PUF, 1989 et Comment l’esprit produit du sens, Paris, Odile Jacob, 2005 ; Danielle Dubois, Sémantique et cognition : catégories, prototypes, typicalité, Paris, Éditions du CNRS, 1991 ; Françoise Cordier et Jacques François, Catégorisation et langage, Paris, Hermès, Lavoisier, 2002.

9 Jean-Pierre Desclés « Implication entre concepts : la notion de typicalité », 1986, et « Réseaux sémantiques : la nature logique et linguistique des relateurs », Travaux de Linguistique et de Littérature, op. cit., 1987 ; Jean-Pierre Desclés et Christine Froidevaux « Axiomatisation de la notion de repérage abstrait », Mathématiques et sciences humaines, N° 78, 1982, pp. 73-119.

10 Voir la note 4. La problématique de la LDO entretient certains rapports importants avec la logique paraconsistante développée par C. A. Da Costa Logiques classiques et non classiques – Essai sur les fondements de la logique, Paris : Masson, 1997 et par J.Y. Beziau, Handbook of Paraconsistency, London, King’s College, 2007. Signalons également les recherches entreprises sur la notion d’objet et son appréhension par Meinong de Brunot Leclerc « Quand c’est l’intension qui compte. Opacité référentielle et objectivité », Bulletin d’Analyse Phénoménologique, vol. 6, N° 8, 2010, pp. 83-108 et « En matière d’ontologie, l’important, ce ne sont pas les gains, mais la participation », Igitur, vol. 4, N° 2, avril 2012, pp. 1-24.

11 Voir Antoine Culioli, Pour une linguistique de l’énonciation. Opérations et représentations, t. 1, Paris, Ophrys, 1990 et Variations sur la linguistique, Paris, Klincksieck, 2002 ; sur l’axiomatisation du repérage abstrait, voir Jean-Pierre Desclés et Christine Froidevaux, « Axiomatisation de la notion de repérage abstrait », op. cit., 1982 ; Jean-Pierre Desclés, « Réseaux sémantiques : la nature logique et linguistique des relateurs », op. cit., 1987.

12 Jean-PierreDesclés, Langages applicatifs, langues naturelles et cognition, Paris, Hermès, 1990, et « Une articulation entre syntaxe et sémantique cognitive : La grammaire applicative et cognitive », Mémoires de la Société de Linguistique de Paris, nouvelle série, Tome XX, Louvain, Peeters, 2011 ; Jean-Pierre Desclés et Zlatka Guentchéva, « Référentiels aspecto-temporels : une approche formelle et cognitive appliquée au français », Bulletin de la Société de Linguistique de Paris, N° 56 (1), 2011, pp. 95-127, et « Universals and Typology », in Binnick Robert (ed.) The Oxford Handbook of Tense and Aspect, Oxford University Press, 2012, pp.123-154.

13 Sur la notion de quasi-topologie, qui étend la topologie en introduisant la frontière interne et la frontière externe d’un lieu, voir, entre autres, Jean-Pierre Desclés et Zlatka Guentchéva, « Quasi topological representations (QTR) of Spatial places and spatio-temporal movements in natural languages », in Z, Marotta Giovani et al. (éds.), Space in Language, Proceedings of the Pisa International Conference, 2010, pp. 213- 233, et « Trimorphe et topologie », inA. Ouattara (éd.), La linguistique de Bernard Pottier : bilan, critiques, perspectives, Reims, Presses Universitaires de Reims, 2011, pp. 218-252. La quasi-topologie trouve une pertinence non seulement en sémantique mais également en anthropologie.

14 Sur la notion de schème sémantico-cognitif (SSC), voir, entre autres, les références de la note 11. Par ailleurs, Bernard Pottier introduit également la notion de schème pour décrire la signification d’unités lexicales dans Représentations mentales et catégorisations linguistiques, Louvain-Paris, Peeters, 2000, et Images et modèles en Sémantique, Paris, Honoré Champion, 2012.

15 La notion de « trimorphe » introduite par B. Pottier est généralisée par le « trimorphe topologique » dans Jean-Pierre Desclés et Zlatka Guentchéva, « Trimorphe et topologie », op. cit. 2011.

16 Voir une analyse détaillée dans Jean-Pierre Desclés, Anca Pascu et Christophe Jouis, « The Logic of Typical and Atypical Instances (LTA) », op. cit., 2013.

17 Les notions de « référentiel » et de « changement de référentiel » deviennent de plus en plus importantes dans l’analyse sémantique, ce qui permet d’unifier de nombreuses analyses. Voir, entre autres, Jean-Pierre Desclés et Zlatka Guentchéva, « Référentiels aspectotemporels : une approche formelle et cognitive appliqué au français », op. cit., 2011.

Illustrations

Titre

Figure 1 : Arbre de Porphyre (un extrait).

URL

https://www.unilim.fr/actes-semiotiques/docannexe/image/5112/img-1.png

Fichier

image/png, 8,1 ko
URL

https://www.unilim.fr/actes-semiotiques/docannexe/image/5112/img-2.png

Fichier

image/png, 7,7 ko
Titre

Figure 2 : Réseaux sémantiques et diagrammes extensionnels correspondants aux énoncés (1)

URL

https://www.unilim.fr/actes-semiotiques/docannexe/image/5112/img-3.png

Fichier

image/png, 7,1 ko
Titre

Figure 3 : Un réseau sémantique.

URL

https://www.unilim.fr/actes-semiotiques/docannexe/image/5112/img-4.png

Fichier

image/png, 5,8 ko
Titre

Figure : 4 : Correspondance entre les extensions topologiques et les intensions, essences et propriété.

URL

https://www.unilim.fr/actes-semiotiques/docannexe/image/5112/img-5.png

Fichier

image/png, 10 ko
Titre

Figure 5 : Chevauchement des frontières externes extensionnelles pour deux concepts voisins‘(…) est-jeune’ et ‘(…) est-vieux’.

URL

https://www.unilim.fr/actes-semiotiques/docannexe/image/5112/img-6.png

Fichier

image/png, 4,4 ko