L’image scientifique : de la visualisation à la mathématisation et retour
Maria Giulia Dondero
FRFC-FNRS, Université de Liège
Index
Mots-clés : allographie, astrophysique, autographie, diagramme, iconicité, indicialité, mathématisation, objet, statut, symbolicité, texte, visualisation
Auteurs cités : Catherine Allamel-Raffin, Michaël Baxandall, Anne BEYAERT-GESLIN, Jean-François BORDRON, Maria Giulia DONDERO, Jacques FONTANILLE, Pierluigi BASSO FOSSALI, Peter Galison, Valeria Giardino, Nelson GOODMAN, Charles Goodwin, Bruno LATOUR, Jean-Pierre Luminet, Mario Piazza, Roger Pouivet, François RASTIER, Félix THÜRLEMANN, Steve Woolgar
Introduction
Je crois que la problématique de l’image scientifique devrait permettre aux sémioticiens de préciser des questions qui avaient été laissées de côtés lors des analyses sémiotiques sur l’image artistique ou publicitaire. La sémiotique du discours en fait a analysé les images sans prendre en compte leurs statuts et leurs pratiques de sémantisation plus ou moins stabilisées, en décidant que c’est directement le regard de l’analyste qui construit la taille sémiotique pertinente pour l’analyse des textes. Cette prise de position peut être expliquée peut-être par une ambition démesurée de constructionisme. De plus, les mêmes outils méthodologiques ont été souvent utilisés de manière indifférenciée pour étudier deux types d’image très différents, l’image artistique et l’image publicitaire par exemple : le niveau de l’objet et donc du médium n’étaient pas pris en compte. Dans le cas des images, par niveau de l’objet j’entends le fait que les configurations visuelles sont toujours enracinées en des supports, et par médium j’entends le fait que les configurations visuelles sont toujours filtrées, et bien au niveau de l’expression qu’au niveau du contenu, par un dispositif communicationnel qui contribue à en déterminer la signification.
En ce qui concerne l’étude de l’image artistique et de l’image publicitaire, une distinction fondamentale aurait pu donc être la suivante : l’image artistique se présente comme objet unique, original, sacralisé, à ne pas toucher et à protéger alors que l’image publicitaire se présente comme objet multiple à afficher, à consommer et à diffuser et multiplier. Cette distinction médiatique aurait permis aussi de distinguer l’effet de sens des supports employés dans les deux cas – toile et papier photographique numéroté dans le cas de l’image artistique ; affiche et papier photographique non numéroté dans le cas de l’image publicitaire.
Jusqu’à ces dernières années, les images artistiques et publicitaires ont très souvent été analysées comme des configurations de formes sans support et sans histoire. Il y a évidemment des contre-exemples dans les deux domaines, même dans les années 80, comme p. e., dans le cas de l’image artistique, l’analyse du Christ mort de Mantegna de la part de Felix Thürlemann (1980) qui, pour expliquer l’iconographie excentrique du Christ de Mantegna, la met en opposition avec la tradition représentationnelle des icônes et en relation étroite avec une série de tableaux de la première renaissance dans la région vénitienne employant des nouvelles solutions de perspective.
En ces dernières années, en sémiotique, grâce surtout aux travaux récents de Jacques Fontanille (2004, 2007, 2008) sur les niveaux de pertinence sémiotique qui remettent en jeu justement les objets textuels, la question du statut s’est imposée comme capitale. On s’est rendu compte que le sémioticien ne peut pas éliminer de son expertise analytique des textes l’identité culturelle de ceux-ci, leur attestation philologique, leurs pratiques d’instanciation et les réseaux des relations que ces textes tissent avec d’autres textes et donc le statut à travers lesquels ils circulent dans la société (ou au moins le statut à travers lequel un texte parvient dans les mains de l’analyste). La prise en compte du statut du texte le transforme en objet culturel et nous oblige en fait à encaisser les niveaux d’analyse. Par statut (documentaire, artistique, publicitaire, scientifique) j’entends le produit d’une grammaticalisation et d’une stabilisation/institutionnalisation des pratiques de production, de sémantisation et d’usage des textes. Ces pratiques d’usages peuvent plus ou moins dépendre des pratiques d’instanciation/production : on sait bien que certaines images peuvent être destinées à la presse ou à un usage privé, p.e. à l’intérieur de la famille, et puis voir détourner leur usage en des images artistiques.
- Note de bas de page 2 :
-
Sur la relation entre image en tant que texte et genre et statut voir Beyaert-Geslin (2009), Basso Fossali et Dondero (2006), Basso Fossali et Dondero (2009) et Dondero (2007).
Contre le déracinement analytique du texte de son origine qui le transformerait en un artifice de la théorie, voire en une confirmation de la théorie, il faut analyser un texte à partir de son attestation historique et de son appartenance à une tradition, qui dépendent toujours des corpora productifs spécifiques (Basso Fossali 2009) ; il faudrait donc reconnecter un texte à son identité culturelle en gardant également le droit de le soumettre aux lentilles grossissantes propres à un dispositif précis d’analyse. D’une certaine manière, on peut affirmer que l’analyse sémiotique des images consistait en une confrontation entre d’une part les choix de l’analyste et de l’autre les constrictions textuelles qui orientaient le parcours de l’analyste (énonciation énoncée). La question délicate, dans la sémiotique greimassienne, était notamment qu’elle postulait la symétrie entre énonciateur et énonciataire, comme si les deux partageaient forcément le même point de vue et la même compétence. Je crois que la symétrie postulée entre énonciateur et énonciataire a contribué à empêcher la prise en compte des statuts, statuts qui construisent une épaisseur sémantique entre l’énonciateur et l’énonciataire et entre ces derniers et l’analyste. Certains aspects étaient exclus de la théorie vu les problèmes méthodologiques qu’ils pouvaient créer ; de plus il fallait à tous prix combattre les vices de l’historicisme. Aujourd’hui, on espère pouvoir réintégrer ces aspects sans forcement trahir les enjeux de la sémiotique classique. En fait la confrontation devrait aujourd’hui se jouer entre quatre instances : le regard de l’analyste (1) les constructions textuelles (2) les statuts des images (3) et leurs genres(4) ; ces deux derniers orientent la relation entre l’analyste et les morphologies du texte2. On a donc une stratification de plusieurs niveaux de pertinence qui concerne différentes grandeurs pertinentes à l’analyse, stratification qui s’étend du statut au genre et au texte. J’entends par genre d’un texte, selon la définition de Rastier, la partie d’un contexte qui peut être considérée comme commune entre ce texte et d’autres textes : il s’agit donc d’une description contextuelle parmi d’autres possibles. Le genre est en somme ce qui permet au texte de se situer dans une situation et d’assumer des statuts. Si, normalement, c’est le statut qui détermine l’orientation sémantique des genres et des textes (si on est tous bien d’accord que le global détermine toujours le local en sémantique), il faut dire aussi que, à un moment donné, le texte peut arriver à transformer les frontières entre les genres et ensuite à moduler les normes statutaires.
- Note de bas de page 3 :
-
Sur l’art comme domaine voir Basso (Fossali) (2002). Pour une théorie des domaines et des rapports entre eux selon l’approche de la sociologie des systèmes sociaux, voir Luhmann (1996). Pour une approche philosophique de la question, voir Pouivet (2000).
- Note de bas de page 4 :
-
Voir à ce sujet Baxandall (1985) qui conçoit la production artistique comme une série de tentatives de répondre à des problèmes internes aux domaines de l’art et de la science .
Notre attention envers l’image scientifique confirme la nécessité d’une approche par stratification de niveaux d’analyse, puisque l’image scientifique demande à l’analyste une compétence sur les pratiques de production et sur l’historique de chaque image (bref, sur la biographie de chaque image). Evidemment, l’image artistique aurait rendu nécessaire aussi cette prise en compte de la part de l’analyste, mais avec l’image scientifique la nécessité se présente comme immédiatement indépassable parce qu’il n’y a aucun accès possible à la signification de l’image sans la prise en compte de la manière à travers laquelle elle s’est constituée en inscription. On pourrait dire aussi que, même si elle ne se constitue pas en inscription au sens classique d’« empreinte de quelque chose », et qu’elle se manifeste par exemple comme une image calculée à partir d’équations (on le verra dans la deuxième partie de notre article), ou bien à partir de théories sur la relativité générale ou d’autres théories également bien acceptées par les communautés scientifiques, sa genèse de fabrication et son appartenance à une tradition de recherche doivent forcement être prises en compte pour faire démarrer l’analyse. En ce sens, il est plus difficile d’extraire l’image scientifique de son contexte de production et de son corpus qu’en extraire l’image artistique. Mais les démarches qu’il nous semblent nécessaires pour étudier l’image scientifique doivent être pensées et transposées aussi à l’image artistique. Ce qui a empêché une telle démarche avec l’image artistique peut s’expliquer peut-être par le fait que l’isolement de chaque image lors de l’exposition au public dans un musée a fait oublier qu’elle n’est pas isolée en tant qu’artefact culturel. En fait, il faut bien comprendre que l’image artistique n’est pas naturellement isolée ; toute image artistique se présente, pour le producteur et le récepteur, et pour la communauté de l’art, comme une nouvelle proposition visuelle, même comme un défi, face à toutes les autres images déjà fabriquées dans le passé et comme une plus ou moins nouvelle manière de répondre à des interrogations présentes dans le monde de l’art. Le prétendu isolement de l’image artistique peut s’expliquer aussi par le caractère autotélique du domaine de l’art3 : l’objet artistique n’a jamais un contexte discursif préfixé ; c’est un discours qui vaut au-delà d’une fonction restreinte par le contexte de production. Enfin, l’art est à soi-même sa fin et chaque œuvre crée un monde possibleindépendant de tous autres. Bref, celui de l’image artistique est un isolement qui révèle notamment des pratiques d’exposition et de valorisation qui lui sont propres, mais qui ne nous légitiment pas à l’étudier comme texte isolé ni à transposer son fonctionnement sur l’image publicitaire ou scientifique. L’isolement d’exposition et de valorisation de l’image artistique ne peut pas se transformer en une méthodologie d’analyse d’un fonctionnement valable pour toute image, comme cela a été le cas dans certaines traditions sémiotiques. D’ailleurs, même en ce qui concerne l’image artistique, il aurait fallu problématiser son isolement d’exposition et le mettre en opposition avec son corpus de sémantisation, c’est-à-dire avec le fait que chaque image artistique répond à des questionnements qui se produisent à l’intérieur d’une tradition de formes et de problèmes à résoudre concernant les paramètres de la représentation4. La même chose arrive aussi pour l’image scientifique, prise toujours à l’intérieur d’un parcours de recherches collectives.
Des attentes des chercheurs dépendent justement les rôles des images scientifiques, rôles qui peuvent être double ou multiple : il faudrait distinguer en premier lieu le rôle qu’une image assume à l’intérieur d’une chaîne d’inscription lors de sa production et de sa négociation en laboratoire et le rôle qu’elle assume lors de la publication des résultats finaux de l’expérience. On va commencer avec les pratiques de production des images scientifiques, en essayant de décrire un parcours modèle de sa stabilisation technologique et institutionnelle.
1. Pratiques d’instanciation. Interrogation, stabilisation, institutionnalisation
- Note de bas de page 5 :
-
« Techniques de transformation, transformation des techniques », colloque international organisé à l’Université de Liège le 23 et 24 octobre 2008 dans le cadre du programme de recherches ANR « Images et dispositifs de visualisation scientifique ».
Venons à présent aux pratiques d’instanciation des images scientifiques. Lors d’un colloque sur les techniques de production qui a eu lieu à l’Université de Liège en octobre 20085, on s’est interrogés sur la production de l’image scientifique en partant de l’idée qu’elle est toujours pénétrée par trois dimensions : 1) la dimension indicielle qui témoigne de ses pratiques d’instanciation, 2) la dimension iconique qui assure à l’image une stabilisation des formes et une méréologisation des données qui pourront transformer les inscriptions des phénomènes en un objet nommableet stabilisé, et 3) la dimension symbolique qui permettrait à chaque image d’être considérée comme le produit négociéd’une pratique communicationnelle institutionnalisée. La dimension symbolique implique qu’on ne puisse pas étudier ni comprendre l’image dans son isolement ; par contre il faut prendre en compte a) les objectifs de sa production, b) les pratiques de recherche d’une discipline, c) les relations de cette discipline avec les institutions, la politique, etc. comme l’expliquent certains travaux fondamentaux en sociologie des sciences de Bruno Latour (1987, 1999, Latour et Woolgar 1979) et de Charles Goodwin (1995, 1996, 1997) en linguistique appliquée et en ethnographie de laboratoire.
Selon cette conception, toute image attestée peut être conçue comme une stratification de ces trois dimensions, la dernière dimension gardant mémoire des deux premières. Même si les dimensions indicielle, iconique et symbolique sont censées être des étapes successives dans le processus de constitution du signe – qu’il soit une image ou non – et donc chronologiquement déterminées, il faut remarquer que chaque dimension peut être focalisée de deux façons différentes. La première envisage justement l’instanciation du signe ; on peut donc entendre l’indicialité, comme chez Jean-François Bordron, comme « la forme sensible de l’interrogation », l’iconicité comme la stabilisation de formes (Bordron 2000, 2004) — donc, d’une certaine manière, comme une réponse aux questionnements perceptifs posés par l’indicialité — et la symbolicité comme le placement de ces formes stabilisées dans un ensemble de règles sémantiques institutionnalisées. La deuxième, plus classique, envisage l’indice, l’icône et le symbole comme des signes déjà constitués se rapportant à quelque autre chose. D’une certaine manière ces deux acceptions peuvent nous être utiles : dans le premier cas on suit la genèse du sens, dans le deuxième cas on est face à un sens déjà constitué, textualisé.
- Note de bas de page 6 :
-
Sur la différence entre disciplines, comme l’astrophysique et l’archéologie, et leurs objectifs fondamentaux voir Allamel-Raffin (2010) et Dondero (2008, 2010)
Dans le domaine de la science, l’image, pour être reconnue comme valable et communicable, doit se constituer à la fin de son parcours productif comme un résultat commensurable par rapport à des attentes, à des hypothèses, bref, aux motivations qui ont rendu nécessaire sa fabrication/investigation. Cela signifie que l’indicialité doit être considérée comme quelque chose qui ne concerne pas seulement l’acte d’instanciation des images, souvent entendu en tant qu’acte d’inscription d’un phénomène sur un support qui est censé en enregistrer les traces. Les degrés d’indicialité d’une image ne peuvent êtreévalués qu’à la fin d’un processus de transformation des inscriptions à partir des utilisations possibles que les images-résultat peuvent remplir et à partir de la place qu’elles peuvent assumer dans un système d’attentes et de résultats comparables avec lesquels ces images-résultats peuvent rentrer en relation. Si donc l’indicialité concerne les traces de l’instanciation, traces qui visent à trouver la « bonne place » dans des configurations, et l’iconicité concerne la stabilisation de formes en objets-images, la symbolicité concerne la place que ces formes stabilisées en objets-images occupent dans un ensemble de pratiques et de procédures institutionnalisées. Plus spécifiquement, la dimension indicielle, qui n’a rien à voir avec l’idée statique d’empreinte ou de contact, est censée nous donner la garantie sur l’accord entre les premières et les dernières transformations et l’iconicité concerne la densité d’enchaînement entre un instrument et l’autre, voire la densité des transductions réussies entre les transformations contrôlées par de paramètres donnés des traces (des phénomènes ainsi que des instruments). L’iconisation concerne en fait un ensemble de transductions contrôlées qui se stabilisent et forment une unité, ce qu’on a appelé toute à l’heure l’objet-image, à savoir l’identification d’une unité d’objet nommable. L’objet est à constituer dans la plupart des disciplines6 et pour que cet objet devienne définissable et de plus en plus stable, voire iconique, il doit être non seulement contrôlable tout au long de ses transformations pendant une expérience, il doit justement nous assurer que quelque chose de constant s’est enfin conservé et a traversé toutes les transformées (Latour). Et l’unité d’objet qui en résulte doit pouvoir garder mémoire de toutes les transformations — et elle doit les rendre répétables par d’autres scientifiques. A la fin du processus toutes les transformations doivent former une congruence de résultats. L’indicialité et l’iconicité peuvent donc devenir mesurables par rapport à un système d’apparitions prévu (symbolicité). D’une certaine manière, on pourrait penser au processus d’instanciation en se posant cette question : est-ce que les inscriptions qui cherchent une commensurabilité entre elles (dimension iconique) et qui sont censées « transporter » la référence d’un point de départ à un point d’arrivée (dimension indicielle), répondent aux objectifs pour lesquels on les a produites (dimension symbolique) ?
2. L’image entre local et global
Passons à présent à un autre stade de l’image ; après son instanciation, et après avoir constitué justement une unité d’objet, elle doit devenir utile pour d’autres recherches, elle doit devenir manipulable. Donc, il faudra briser cette unité…
- Note de bas de page 7 :
-
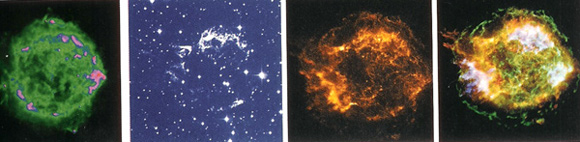
de gauche à droite : NRAO/AUI ; MDM/R. Fesen ; NASA/CXC/SAO ; NASA/CXC/SAO ; http://chandra.harvard.edu/photo/1999/0237/
- Note de bas de page 8 :
-
http://imgsrc.hubblesite.org/hu/db/2006/51/images/a/formats/print.jpg
Il me semble que l’astrophysique exemplifie bien ce mouvement double ; en fait la fabrication d’images en astrophysique nous montre bien le va-et-vient entre la visée locale et la visée globale des visualisations : d’une part, l’horizon de l’astrophysique est de présenter en unité, de compacter, par le biais de l’image justement, des fonctionnements dispersés dans le temps et dans l’espace (visée localisante) ; d’autre part, cette unité est constituée en modules « locaux » : chaque module est une réponse de l’« objet », par exemple, l’objet-supernova (PHOTO 1)7, à la longueur d’onde avec laquelle il a été détecté. Les différents modules composent des images finales, intégrées : voici l’image finale d’un amas de galaxies et les modules dont elle se compose (PHOTO 2)8. Pour obtenir cette image qui nous donne l’iconographie finale d’un amas de galaxies, il a fallu un travail orienté du simple au composé, mais d’autre part, cette totalité intégrée qui est l’image finale doit pouvoir êtrelittéralement redistribuée via une autonomisation de ses modules pour qu’ils puissent être utilisables pour la constitution d’iconographies autre que celle de cet amas de galaxies (visée globalisante). Il s’agit de réaménager les modules qui ont, de leur côté, une certaine cohérence interne et une homogénéité de paramétrage (ici, la même longueur d’onde) pour voir s’ils sont aptes à construire d’autres iconographies, et ensuite, on pourrait dire, à « faire avancer le référent » (Latour 1999), à étendre sa chaîne de transformations, et aussi à mettre à l’épreuve l’utilisation transversale de chaque module paramétré.
Résumons : d’une part, il faut discipliner les opérateurs de la chaîne des transformations et les aligner de façon à ce qu’ils forment une unité, pour que la chaîne puisse se constituer en une unité stable (iconicité) et produire un objet (symbolicité), mais il faut penser aussi au pouvoir d’extension du référent que la visualisation offre à la science, à savoir le fait que cette unité d’objet stabilisée en image peut servir comme modèle pour d’autres investigations. Or pour servir de modèle pour d’autres investigations, il faut que cette unité puisse se décomposer en des sous-unités ré-articulables, en des modules justement, et que ces modules puissent devenir des éléments ré-combinables d’une grammaire visuelle :éprouver la solidité d’un fait, c’est le mettre à l’épreuve et l’étendre plus loin par un nouveau branchement de ces modules. Les possibles combinaisons entre modules et les règles qui les gèrent peuvent se constituer en un système comparable à une grammaire. On peut donc enfin affirmer que l’image scientifique doit être entendue non seulement en tant qu’indicielle, voire en tant que produit qui conserve quelque chose de constant à travers les transformées, mais en tant que résultatdes transformations parcourues qui ont trouvé une stabilité et un accord entre elles (dimension iconique). C’est ensuite l’iconicité qui donne la légitimation à l’image par rapport aux attentes des chercheurs, qui situeront cette image dans un système encyclopédique (dimension symbolique). A partir de là, il faudra voir quels sont les développements possibles de ces images. D’un côté, la bonne réussite de la chaîne de transformations assure une garantie de contrôle réciproque entre phases techniques, et donc la garantie d’une histoire de production par contigüité (indicialité) et par commensurabilités (iconicité), de l’autre, le résultat de cette chaîne de transformations doit assurer des développements des recherches (symbolicité).
Dans l’image finale de l’amas de galaxie qu’on a vu tout à l’heure, les éléments sont intriqués et c’est justementla modularité typique de l’astrophysique qui permet à l’unité de l’image finale d’extraire ses modules et de les transporter au loin, vers d’autres compositions. De les transporter au loin grâce au pouvoir grammatical des modules, entités recombinables à l’instar de notes dans une partition de musique qui doivent servir comme des instructions pour l’exécution future, qu’elle soit visuelle ou sonore.Cela revient à dire que le travail scientifique consiste bien, dans un premier temps, en la recherche de la stabilisation en unité d’objet et, ensuite, dans un deuxième temps, en la manipulation de cette unité, recombinaison, ré-articulation de ses modules, pour la faire « courir au loin » (Latour), pour construire d’autres unités et d’autres référents.
La nécessité d’une modularité s’explique aussi par le fait que la chaîne des transformations, qui vise à une stabilisation, doit pouvoir être réversible, les scientifiques doivent pouvoir revenir sur leurs pas : c’est une communauté entière qui doit pouvoir manipuler la chaîne dans toutes ses étapes. C’est pour cette raison qu’il faut constituer une notationnalité, une sorte d’alphabet d’opérations paramétrées, pour que ceux qui font partie de la communauté puissent poursuivre la chaîne, la renverser, la refaire, la contrôler, la valider.
Les images doivent permettre premièrement d’identifier et de fixer des phénomènes (autographie) et surtout de les définir en tant qu’objets dont on peut discuter, et deuxièmement de travailler sur ces objets justement, objets qui peuvent servir comme des expériences de pensée, voire comme des objets qui se prêtent à lamanipulation (allographie). Les images réussies deviennent ainsi des terrains de travail opérables, dans le sens qu’elles sont non seulement des visualisations d’opérations qui rendent possibles la définition de phénomènes (et on a là la constitution des valeurs opératives d’une image et l’accomplissement de ce qu’on a nommé lavisée locale de l’investigation), mais elles fonctionnent aussi comme des visualisations qui permettent d’être retravaillées et manipulées pour des fins ultérieures (visée globale). De l’image comme produit stabilisé des transformations on passe au potentiel transformationnel, de l’image comme zone de stockage on passe à une zone d’opérabilité et de manipulation.
Comment pourrait-on qualifier cette relation qui garde ensemble l’enracinement de la production de la trace (autographie) avec la transponibilité des résultats de l’investigation visuelle par le biais de la modularité (allographie) ?
3. L’image entre autographie et allographie : le diagramme
3.1 De l’empreinte à la mathématisation
- Note de bas de page 9 :
-
« Collection Cinémathèque française, Paris ».
- Note de bas de page 10 :
-
Pour une analyse de la production de Marey entre buts scientifiques et artistiques, voir Dondero (2009).
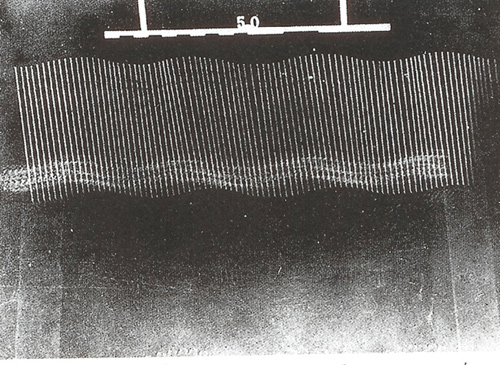
Il faut dire que cette relation entre enracinement de la trace (autographie) et notationnalité des modules (allographie), entre visée locale et globale, nous amène évidemment à porter notre attention sur la relation entre visualisation et opérations de digitalisation jusqu’à la mathématisation. Il s’agit de la relation entre la possibilité de visualiser des résultats locaux et la nécessité de les rendre transmissibles, bref, de les rendre utilisables pour des enjeux ultérieurs, non-locaux. Ce rapport est envisageable dans l’imagerie, mais il est déjà présent dans le dessin millimétré et dans la chronophotographie. Même si la photographie classique pouvait apparaître comme un dispositif qui ne permettrait que de construire des relations locales, à savoir entre un objet et une image, bref, entre un particulier et un autre particulier, la chronophotographie de Jules-Etienne Marey, par contre, a pu augmenter la possibilité de contrôle des données et ensuite celle de faire des hypothèses mathématiques sur le rapport entre espace parcouru et durée. Voici l’Etude de la marche d'un homme avec une baguette blanche fixée le long de la colonne vertébrale (1886) (PHOTO 3)9. La chronophotographie a pu coupler la prise locale (c.-à-d. la prise de l’empreinte, ici le trajet en bas en continu) avec la mesurabilité de cette empreinte même (la répétition de la baguette en mouvement), mesurabilité qui est déjà un instrument de traductibilité, reproductibilité, transmissibilité : cette chronophotographie garde ensemble les détails locaux de l’empreinte et en même temps construit des discontinuités au sein de cette empreinte10. Ce sont ces discontinuités qui permettent de construire une notation qui amène chaque chronophotographie à se dépasser elle-même : en passant par une notationnalité garantie par sa partie graphique, à savoir par la constitution de rapports spatio-temporels codés, elle peut devenir un texte d’instructions pour l’investigation et la comparaison d’autres phénomènes spatio-temporels que ceux concernant ce mouvement précis ici photographié.
- Note de bas de page 11 :
-
« Collection Cinémathèque française, Paris ».
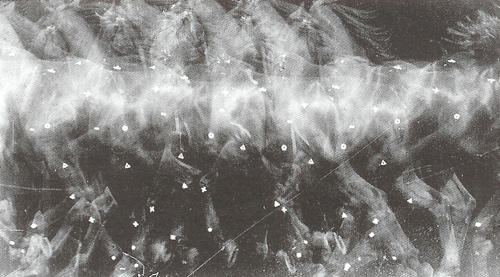
Voici une autre chronophotographie de Marey, l’image d’un cheval au trot, Étude du trot du cheval (1886) (PHOTO 4)11 : cette chronophotographie est censée capter l’empreinte du mouvement particulier de ce cheval précis (on voit le flou du mouvement), mais la partie graphique (visualisée en tant que réseaux de points blancs) résultante du mesurage de la relation entre espace parcouru et durée de ce parcours fait d’intervalles, permet une analyse du mouvement dans la durée qui fonctionne comme une opération d’allographisation de ces données spatio-temporelles particulières. La notation est la constitution d’un alphabet de modules qui vise à offrir un plan de commensurabilité entre particularités ; il ne s’agit pas spécialement de généralisations, mais justement des commensurabilités, et de la possibilité de caractériser une image non seulement comme une image de quelque chose, mais comme un terrain d’opérations possibles en vue de manipulations ultérieures. Cette chronophotographie nous montre bien que la configuration graphique peut être littéralement contenue dans l’empreinte photographique et, même, que ces deux configurations de l’image (à savoir la densité figurative de l’empreinte et les rapports mesurables entre espace et intervalle temporel) peuvent cohabiter et profiter l’une de l’autre afin de visualiser un interstice de commensurabilité entre les données locaux et les patterns qui sont la source d’une grammaire de rapports entre espace parcouru et durée. L’allographisation d’une image ou d’une série d’images permet de sélectionner des relations de données, d’extraire des règles et de rendre enfin transposables les résultats d’une investigation et de fabriquer par conséquent d’autres images. L’image, en s’allographiant, devient comparableavec d’autres images, manipulable et orientée au futur. En affichant des patterns et des régularités, elle peut devenir ainsi une image prédictive. Pour répondre à la question qui s’est posée à la fin du chapitre précédent, les chronophotographies sont des visualisations qu’on pourrait qualifier enfin de diagrammatiques, en empruntant de Nelson Goodman (1968) le sens du terme diagramme. Le diagramme valorise en même temps le support des données (densité figurative, autographie) et la possibilité de rendre les rapports entre ces données des véritables exemplifications pour d’autres pratiques d’investigation — dans le régime de l’allographie, évidemment, le support des inscriptions n’est plus pertinent, l’inscription perd par conséquent sa densité. Des données et de leurs ancrages dans une phénoménologie des expériences vont être extraits des patterns qui nous permettraient de construire des notations (allographie). Ce qu’on extrait des images autographiques ce ne sont pas des données, mais sont justement des relations entre données, des équivalences, des moyennes, bref des fondements pour des comparabilités futures. Et le diagramme se situe au milieu de ces deux stratégies de représentation : entre la densité et la notation, entre une opération de densification (image qui vise à expliquer ou résoudre des cas précis) et une opération de grammaticalisation (image prédictive). La caractéristique la plus générale du diagramme est bien qu’il combine les détails et les patterns, il visualise le rapport entre moyennes et variations. Le diagramme laisse ouvertes les deux portes : la porte de la densité et du localisme, et la porte de la grammaticalisation ; il permet ainsi un regard anamorphique. Comme l’affirme Pierluigi Basso Fossali (Basso Fossali et Dondero 2006), le diagramme est une forme abstraite de relation qui est exemplifiée dans l’expérience et transposable pour d’autres expériences.
3.2 De l’équation à la visualisation dans l’astrophysique des trous noirs
Je voudrais à présent porter mon attention sur un parcours inverse, qui va du général au local, de la mathématisation à la visualisation, visualisation qui n’est pas forcement synonyme de localisme : il s’agit en fait d’un local pluriel. Je quitte la chronophotographie pour revenir à l’astrophysique et notamment aux démarches de la physique théorique, qui vise à rendre concevable un objet de recherche très spécial, objet non seulement invisible, mais aussi objet dont l’existence n’est que supposée à partir d’autres phénomènes cosmologiques auxquels on cherche des explications. Il s’agit des trous noirs, objet théorique par excellence. Comme tout le monde le sait, il est impossible de filmer ou de photographier un trou noir : les trous noirs sont a priori parfaitement invisibles et leur existence n’est que supposée. La matière étant constituée de vide entre les atomes, dans un trou noir elle se condense de telle sorte que le vide disparaît entre les atomes. Dans le cas du trou noir, la matière s’effondre sur elle-même et la force de gravitation l’emporte sur les autres, ce qui fait que tout ce qui approche un trou noir y disparaît. Un rayon lumineux par exemple est alors complètement absorbé. Le trous noirs sont enfin une sorte de gouffre qui attire la lumière, on ne peut donc jamais les photographier puisqu’ils n’émettent aucune lumière.
- Note de bas de page 12 :
-
Je remercie vivement Jean-Pierre Luminet pour m’avoir accordé les droits de reproduction des images et des schemas des trous noirs.
Dans un article de 1979 intitulé « Image of a Spherical Black Hole with Thin Accretion Disk », publié dans la revue Astronomy and Astrophysics, Jean-Pierre Luminet, célèbre astrophysicien qui travaille à l’Observatoire de Paris Meudon, propose pour la première fois une iconographie (PHOTO 5)12 des trous noirs, trous noirs au pluriel. Cette iconographie finale se présente comme rien d’autre qu’un produit des connaissances en relativité générale sur la topologie cosmologique d’une part et en mathématique de l’autre : cette iconographie n’est enfin que le résultat d’une série d’équations. Luminet construit tout au long d’une dizaine de pages ce qu’on pourrait nommer un véritable parcours d’« iconographisation » à travers une série d’expériences — qu’il nous fait partager de manière très ponctuelle. Avant de prendre en compte ces expériences de près, je me permets de rappeler que la mathématique ne fait pas partie des sciences observationnelles, qui sont des sciences qui fondent leurs théories justement sur des expériences en laboratoire, mais elle est une science formelle, déductive. On s’apercevra que, dans le domaine de l’astrophysique, cette distinction se présente à plusieurs égards fallacieuse, comme le montre à notre avis cet article de Luminet de 1979, où la mathématique se révèle comme une sciences déductive bien sûr, mais en même temps liée à la visualisation de ses propres valeurs et à l’observation(Galison, 2002 ; Giardino et Piazza 2008). Observation et visualisation non pas d’une réalité supposée extérieure mais, au contraire, d’une réalité explicative et prédictive de certains phénomènes, réalité explicative qui, pour devenir opérationnelle, a besoin d’être spatialisée. Toute spatialisation géométrique a l’avantage de visualiser les manières dont les différents éléments et valeurs se structurent et s’organisent ensemble dans un espace qui constitue une totalité,même locale,et qui a le pouvoir de rendre visible la relation entre les valeurs, d’en marquer des ajustements possibles, d’en suivre le parcours des transformations contrôlées et systématiques. Il s’agit d’ailleurs en mathématique de spatialisations qu’il ne faut pas considérer comme particularisantes, voire comme des cartes qui « souffrent » d’un excès d’informations susceptible de déranger le raisonnement mais, tout au contraire, comme des visualisations qui permettent de généraliser et modéliser l’information, donc de théoriser. Des visualisations qui permettent aussi, comme on le verra, de rendre l’information manipulable. De plus, il faut remarquer que la mathématique en physique théorique rend pertinente l’observation aussi d’un autre point de vue : non seulement elle se manifeste comme une science qui se fonde sur la visualisation des valeurs des équations, mais elle est aussi une disciplines dont on peut observer les pratiques, pratiques qui ne sont pas du tout exclusivement mentales, mais aussi externalisées en des gestualités observables par l’anthropologue ou le sémioticien. Ces gestualités impliquées dans la visualisation permettent aux mathématiciens de travailler de manière collective sur des mêmes données. Les pratiques mathématiques peuvent elles-aussi être considérées comme constituant un laboratoire en elles-mêmes, un laboratoire où les instruments sont des crayons, du papier millimétré, mais surtout des ordinateurs qui permettent des simulations et fournissent des « preuves numériques ». En tout cas ces instruments sont de lieux de manipulation et de contrôle de valeurs/paramètres, ainsi que de partage et de négociation des décisions.
3.3 Analyse de « Image of a Spherical Black Hole with Thin Accretion Disk » (1979)
Revenons à présent au texte de Luminet, « Image of a Spherical Black Hole with Thin Accretion Disk », afin d’expliquer mieux l’affirmation, qui peut paraître au premier abord paradoxale, sur le caractère pluriel de l’image en physique théorique.
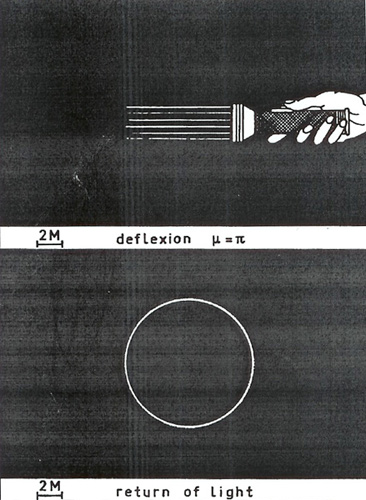
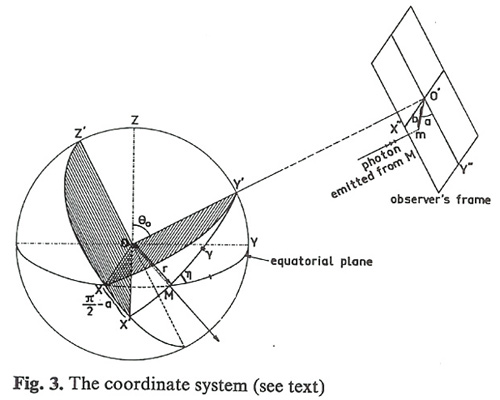
Etant le trou noir invisible à toute longueur d’onde, Luminet nous propose dès le début de son article de concevoir la manière dont un trou noir de certaines dimensions arbitrairement données pourrait réagir à un certain éclairage artificiel donné, projeté par une source lointaine. Les équations dans le texte sont censées expliquer comment il est possible, à partir d’une position d’observation donnée, de calculer l’angle de déflexion et de là de commencer à concevoir visuellement les contours d’un trou noir sphérique, comme on le voit dans cette image construite sur deux points de vue (PHOTO 6). En fait, cette image double nous montre en haut l’acte d’éclairage par une source choisie (acte d’instanciation) et ensuite, en bas, le résultat de cet acte d’éclairage, à savoir le résultat de la vision du trou noir qui peut être obtenue par un observateur dans une position tout aussi calculée (acte de réception). Le texte écrit explique comment l’observateur peut remplir des positions spatiales dans l’image : de ce point de vue, le texte dispose,à travers les chaînes d’équations, des positions d’observationque l’image est censée mettre en scène. A ce propos, une phrase qui suit une série d’équations et annonce l’image nous apparaît au premier abord comme étonnante : « We shall see below [dans l’image] the observational consequences of this fact » (Luminet, 1979, p. 229). On s’aperçoit que ce sont les équations qui donnent des instructions en vue d’un déploiement spatial qui se concrétise dans des dispositifs qu’on peut appeler, pour le moment, génériquement, images. C’est dire que le texte de l’article de Luminet décrit la traduction d’un certain nombre d’équations en des dispositifs spatiaux qui mettent en scène les conséquences observationnelles de certains faits mathématiques construits par les équations elles-mêmes. C’est dire que les équations apparaissent comme des produits d’une théorie générale de la relativité et ensuite elles sont censées elles-mêmes produire des faits mathématiques. Mais ces faits deviennent partageables et communicables pour les recherches en astrophysique lorsqu’ils deviennent observables. Dans le cas précis de l’article de Luminet, les équations, pour se dire opératives, et les faits pour se dire « effectifs » et efficaces, doivent pouvoir déboucher sur des dispositifs visuels. Cette image double montre non pas le trou noir en soi, mais les démarches qui nous permettent de le constituer en un fait et de le visualiser en tant qu’objet — à savoir l’acte d’éclairage et l’acte d’observation contrôlés par des paramètres mathématiques stricts — : d’ailleurs le trou noir est quelque chose de littéralement non visible et Luminet est obligé de le représenter par les actes énonciatifs qui devraient permettre de le rendre visualisable à la fin du parcours. Le trou noir se manifeste dans l’image en bas comme un trou quel qu’il soit, voire comme un espace vide entouré d’un contour qui est le produit de l’acte fictif d’éclairage et de la réception fictive de cet acte d’éclairage de la part d’un observateur placé dans ce but à 180° du trou noir. Il en résulte que le trou noir peut exister pour nous comme le produit de la rencontre d’une source de lumière et d’une position d’observation : l’existence du trou noir résulte de cette image composée de rien d’autre qu’une confrontation de forces et de positions énonciatives calculées et fictives. L’image double nous propose donc une exemplification de ce qui est censé être un trou noir, à savoir un système de forces plus ou moins en équilibre, qu’on ne peut étudier, comme tout phénomène physique, qu’à partir d’un acte provocateur (éclairage/exploration) et ensuite par la visualisation des réactions à cette provocation. Ce dispositif d’investigation, fait de provocations simulées à l’ordinateur et de réactions tout autant simulées à ces provocations, est constitutif de la structure minimale de l’expérience en laboratoire, l’expérience en laboratoire étant notamment une question de stimulations paramétrées et de récolte/enregistrement/traitement des résultats de ces stimulations. L’image d’en bas nous offre la vision d’une sphère noire aux contours lumineux entourés d’un espace également noir. L’observateur est « englobé » dans cet espace de l’expérience mentale, expérience mentale qui est pourtant chromatiquement et topologiquement caractérisée : le simple fait que l’espace soit représenté comme noir montre bien que l’auteur construit cette expérience mentale en essayant en même temps de la rendre le plus possible particularisée et enracinée dans une phénoménologie de la perception. L’œil n’est donc pas un organe mathématiquement non-pertinent : le raisonnement mathématique n’est pas séparé des formes d’expériences sensorielles.
L’image qui suit (PHOTO 7) n’est plus construite à partir du point de vue d’un observateur (à savoir d’un point de vue incarné dans une pratique de vision qui, même mentale, est également enracinée dans une topologie caractérisée) : cette image — pour l’appeler encore une fois avec un nom très générique — est construite par le biais d’un point de vue de nulle part, voire par un point de vue de Dieu. J’entends par point de vue de Dieu le résultat d’une vision qui montre la place d’un observateur modèle sans que cette place puisse être assumée par l’observateur de l’image. En fait, l’observateur modèle n’est même pas censé être un point de vue, mais un lieu générique situé dans la partie droite de l’image : l’image contient en fait un « observer’s frame » très générique. Le texte confirme notre remarque car il récite ces mots : « Assuming that the observer is practically at infinity and at rest in the gravitational field of the black hole… » (ib. p. 230). L’observateur du trou noir n’est pas identifié par des coordonnées spatiales que nous les observateurs/lecteurs pouvons occuper, comme c’était par contre possible dans le cas de l’image double vue précédemment où nous, les lecteurs de l’article, pouvions occuper la même place que l’observateur fictif du trou noir. L’image précédente nous mettait dans une position frontale par rapport à l’objet à saisir ; par contre dans cette dernière image on a une méta-vision sur la place destinée à l’observateur ; l’observateur énoncé assume une position incertaine, à l’infini (at infinity), position diffuse dans le champ de la gravitation. Cette image fonctionne pour le moment plus comme une image-schéma sans point d’observation privilégié que comme un image-diagramme qui viserait, par contre, à enraciner l’observateur en lui offrant une position précise à assumer. Pour expliquer ce que j’entends par image-schéma et image-diagramme, il me faut revenir à la distinction de Nelson Goodman (1968) concernant les régimes autographiques et allographiques de la signification. Le régime autographique concerne un type d’image qui garde en elle-même les traces de son acte d’instanciation de la part d’un énonciateur. L’image autographique témoigne d’un acte d’instanciation particulier ; dans le cas de l’image scientifique, d’un mesurage particulier, d’une prise de vue, bref d’une situation locale et non répétable. Le régime allographique de l’image, ou mieux d’une série d’images, concerne la répétabilité, reproductibilité, transposabilité des résultats de l’investigation visuelle par le biais de la modularité.
Pour revenir à l’image-schéma et à l’image-diagramme, l’image-schéma appartiendrait selon les paramètres de Goodman plutôt au régime allographique, où l’image perd toute relation avec son support d’inscription et avec la situation locale qu’elle est censée représenter, pour pouvoir devenir un outil d’exemplification et de comparaison ; l’image-diagramme par contre appartiendrait aux véritables lisières du régime autographique, régime qui s’étend entre deux pôles en tension : la pictorialité (maximum de densité syntaxique et sémantiques des éléments qui composent l’image) et la diagrammaticité justement (minimum de densité syntaxique et sémantique des éléments qui composent la trace en image). La diagrammaticité est censée établir une connexion entre enracinement de la trace (autographie) et notationnalité des modules (allographie), entre visée locale et globale, bref, et pour le dire de manière simplificatrice, entre particularité et généralité. La diagrammaticité devrait assurer une intra-vision entre l’inhérence du support d’inscription et la transposabilité des données et dans ces cas, des valeurs, pour poursuivre les comparaisons et le déclenchement d’autres recherches.
3.4 De l’équation à la visualisation
- Note de bas de page 13 :
-
Il a été remarqué, en ce qui concerne la géométrie fondamentale, que le diagramme fonctionne de manière très différente du plan urbain par exemple ; comme lui, il indexe quelque chose : là il y a une bibliothèque, là il y a un angle obtus. Mais le plan n’ambitionne pas de promouvoir des inférences spatiales sur d’autres villes dont il n’est pas la carte. Par contre, un diagramme qui représente un triangle rectangle dans une démonstration du théorème de Pythagore ambitionne de concerner tous les autres rectangles parce qu’il représente un triangle « générique », c’est-à-dire une règle de construction (voir Giardino-Piazza 2008 à ce sujet). Il a été observé que la somme des angles internes d’un rectangle est de 180°, où « l’article indéterminatif ne concerne pas une lecture de re (triangle spécifique), mais il reçoit automatiquement une lecture de dicto (triangle générique), lecture fondée formellement par un quantificateur universel » (ibidem, p. 92). Il s’agit du résultat de la rencontre entre « les propriétés nécessairement particulières d’un diagramme et la validité générale du théorème qui résulte de la démonstration qui utilise ce diagramme » (ib. p. 90). Giardino et Piazza expliquent ce caractère général du théorème par une « invariance pratique » et par une répétition que le diagramme permet d’effectuer : « La démonstration concerne en fait une classe générale d’objets, dans la mesure où elle peut être facilement répétée pour des objets géométriques qui en satisfont les mêmes conditions. Bref, la généralité géométrique consiste en la certitude que des constructions particulières peuvent être répétées : la généralité consiste en une invariance pratique » (ib. p. 93).
Si on poursuit la lecture de l’article de Luminet, on s’aperçoit que ce sont les équations rythmant le texte écrit qui sont censées reconstruire, par des coordonnées mathématiques (domaine de l’allographie), un point de vue précis et localisé (domaine de l’autographie) qui paraît manquer à ce qu’on vient d’appeler l’image-schéma. En fait, la légende de cette image reprend ces mots : « The coordinate system (see text) ». C’est l’équation, indexée par l’image-schéma, qui est censée offrir un point de vue incarné à cette même image-schéma, en la transformant justement en une image-diagramme : l’équation nous fournit les coordonnées spatiales qui pourront remplir la position de l’observateur. La phrase entre parenthèse « see text » montre de manière éclairante que les données de lavisualisation sont partagées par le texte et par l’image. D’une certaine manière on pourrait dire que l’équation détermine et localise l’image-schéma en lui offrant les coordonnés précises d’observation ; l’équation (allographie) semble offrir à l’image elle-même une particularisation, un enracinement (autographie). A première vue, c’est un fonctionnement étonnant, parce que l’image a toujours été considéréecomme plus dense d’information (densité syntaxique et sémantique de l’autographie) que le texte verbal et l’équation (possibilité d’identifier des éléments disjoints). C’est quelque chose qui nous étonne parce que pendant des siècles, comme le témoignent les études de Peter Galison (1997 et 2002), les scientifiques ont lutté contre l’utilisation de l’image dans le processus de la démonstration dans les sciences formelles parce que l’image était censée être victime d’un insurmontable localisme dû notamment à son enracinement spatial. Mais on s’aperçoit que dans ce cas-ci l’équation localise l’image, et l’image peut généraliser l’équation (fonctionnement diagrammatique). En fait, l’image-schéma offre une vision de nulle part et les équations et le texte explicatif aident à spatialiser mieux le rendu visuel en explicitant les contenus des équations. L’image et le texte échangent ainsi leurs rôles. L’équation densifie l’image, et cette dernière y gagne un pouvoir de généralisation plus fort que la première. Dans ce mouvement, le schéma devient diagramme, c’est-à-dire une construction mixte : ni uniquement visuelle, ni uniquement verbale, ni uniquement autographique ni uniquement allographique, ni totalement locale, ni uniquement abstraite de tout support d’inscription. Tout diagramme en fait est lié à des propriétés locales de l’espace (position, dimension, orientation et d’autres détails spatio-temporels) mais en même temps il ambitionne de valoir pour plusieurs dispositifs (tous les rectangles dans le cas du théorème de Pythagore, par exemple)13.
Mais revenons aux stratégies de densification de l’image par la description écritedes équations. Une des stratégies les plus étonnantes est celle qui densifie l’image en décrivant via le texte écrit ce qui est normalement le rendu le plus évident de l’image : la mise en scène de la lumière. Le texte affirme : « It follows from the above discussion that rays that reach the observer will give a picture consisting of a black disk of radius… surrounded by ‘ghost’ rings of different radius and brightness » (p. 230). Ensuite : « The external ring is the brightest one; as wee see from (8), the brightness decreases exponentially from the external ring to the internal one ». Quand on revient à (8) on ne trouve pas un schéma ou une image, mais justement une équation. De plus, à la fin de la section, l’auteur affirme : « This is not only matter of brightness, but also a matter of resolution ». On comprend bien que la relation entre texte écrit et visualisation n’est pas du tout du genre qu’on imagine normalement, notamment en mathématique ou dans les domaines qui concernent des entités considérées comme ne possédant qu’une existence mentale, ou bien déductive : en fait, il ne s’agit pas d’un texte écrit qui décrit et argumente quelque chose et qui ensuite en montre l’image comme résultat de la description, mais tout au contraire l’argumentation du texte écrit progresse par le biais d’actes de visualisation. C’est la visualisation qui guide l’expérience, même si ce sont les équations qui donnent les coordonnées précises de cette visualisation. Ce qui est étonnant est que le texte écrit renvoie aux équations qui sont censées spécifier l’image, contre l’idée reçue que l’image est toujours, à cause de son ancrage dans un espace particulier, quelque chose de plus locale dont il faut s’éloigner si on veut procéder aux calculs, aux équations, bref à la généralisation. Ici ce sont les équations qui donnent ancrage à la spatialité qui, sans ces dernières, resterait trop générale, généraliste. D’une certaine manière, on pourrait conclure que les contenus des équations sont bien des visualisations et que les visualisations offrent une forme aux équations. C’est le texte écrit qui se charge de la traduction qui va de l’équation à l’image, et qui produit une ekphrasis préventive qui a comme résultat, et pas comme point de départ, une image. C’est comme si le texte écrit essayait de rendre une vision produite par l’équation et de la visualiser spatialement : mais, comme on l’a déjà dit, le but n’est pas d’obtenir une image plus précise, plus locale, plus ancrée : l’image permet plutôt de cerner un espace où des manipulations des valeurs et des paramètres peuvent moduler la manifestation. C’est l’équation qui donne l’ancrage que l’image ne peut pas produire toute seule, mais c’est en revanche l’image qui offre aux équations un espace opérable, voire un espace d’expérimentation.On va voir tout de suite que la visualisation offre bien sûr la forme aux valeurs des équations, mais en offre une forme manipulable, et une forme déclinable au pluriel.
3.5. L’espace manipulable du diagramme
- Note de bas de page 14 :
-
Ces images montrent aussi, par le biais de lignes hachurées, les configurations spatiales qui doivent exister mais qui ne sont pas visibles de la part de l’observateur modèle placé dans les positions données.
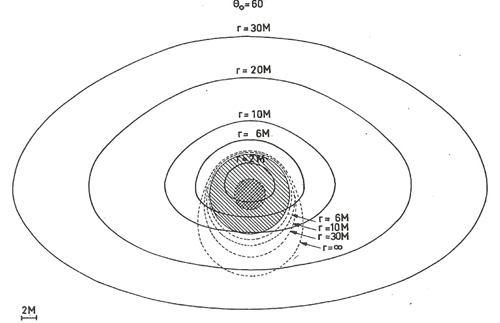
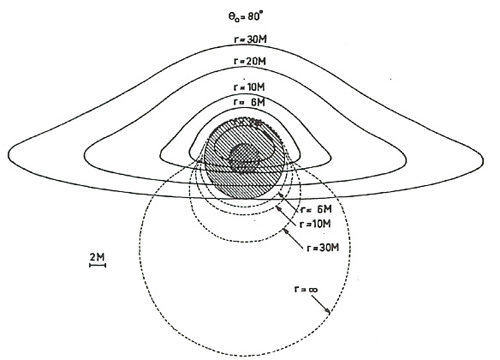
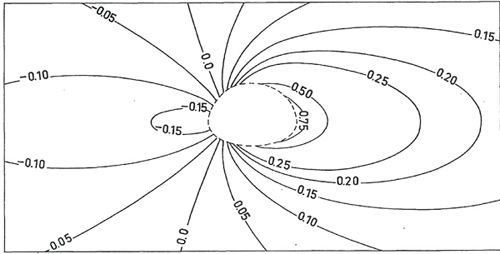
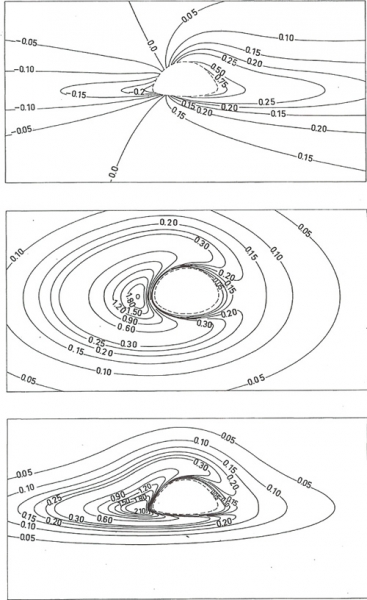
Si jusqu’à maintenant Luminet s’est occupé de décrire une lumière abstraite illuminant le trou noir, à savoir une lumière qui n’existe pas dans l’espace de l’univers ; dans les pages qui suivent il conçoit un disque d’accrétion comme source de radiation. Ce disque est censé, selon les règles de la relativité générale, orbiter autour du trou noir. Luminet envisage donc d’étudier les trous noirs à partir de cet objet gazeux compact qui l’entoure et qui est l’un des processus considérés comme d’importance majeure dans l’astrophysique des hautes énergies. Luminet nous offre une série d’images qui sont encore une fois le résultat d’équations. Ces images mettent en scène les différentes positions possibles de l’observateur (PHOTOS 8-9-10-11), dont seulement les visualisations en série peuvent montrer les relations : c’est-à-dire que la visualisation peut, à la différence de l’équation, visualiser les différents paramètres des calculs, les relations entre eux et spatialiser ainsi la relation entre les résultats des manipulations de ces paramètres, manipulation qui est une manipulation systémique. La transformation systémique des paramètres permet de visualiser des transformations visuelles cohérentes, voire des patterns qui peuvent aboutir à une image qui fait la synthèse de l’ensemble des paramètres expérimentés, qui soit en fait une image, comme le dit Luminet, produite par l’ensemble des résultats obtenus14. Le diagramme permet de visualiser la manipulation des paramètres de contrôle de l’expérience même. Les relations entre les éléments et les valeurs de l’image-diagramme deviennent des patterns autonomes qui ont une existence autonome mais en même temps sont régulés par la totalité de l’espace dans laquelle ils se trouvent organisés : il s’agit d’une partition de symétrie grâce à la connectivité de l’espace (Giardino et Piazza, 2008, p. 86). Pour poursuivre les expériences, ces patterns peuvent être transposés dans d’autres totalités spatiales construites sur d’autres règles de représentation et de manipulation.
La dernière page de l’article montre ce que Luminet appelle « photographie simulée d’un trou noir entouré par un petit (thin) disque d’accrétion » (PHOTO 5). Dans les dernières lignes de l’article Luminet affirme que ces trois dernières visualisations peuvent valoir pour un large nombre de trous noirs, et il précise : « our picture could represent many relatively weak sources ». L’image est ainsi conçue en tant que modèle d’un certain type de trous noirs : c’est pour cette raison qu’on a parlé d’une iconographie finale des trous noirs au pluriel au tout début de notre article, et ensuite d’une forme plurielle de l’image-diagramme manipulable. Cette image montre en fait une iconographie stabilisée de tous les résultats d’équations et pour la comprendre il faut se rappeler comment cette image a été composée ; elle est le produit de la composition de la moyenne des paramètres visualisées dans les images précédentes, qu’on pourrait à nouveau déployer et puis recomposer. Elle est une image qui n’offre pas une vision simultanée d’un trou noir, mais offre au contraire une invariante par le biais de laquelle plusieurs trous noirs qui partagent la même source de radiation peuvent être représentés et expérimentés. Ici on a affaire avec des images prédictives, avec des images-modèles en quête de leurs référents. On peut en outre affirmer que l’article de Luminet n’est pas seulement syncrétique dans le sens qu’il met en relation des visualisations et du texte écrit, des configurations analogiques et des éléments digitaux et disjoints, mais il est aussi synesthésique parce qu’il offre la visualisation des transformations de paramètres et de points de vue. Comme tout diagramme, ces images peuvent être comprises seulement si on les utilise comme terrain d’expérimentation cinétique et sensori-moteur.
Pour conclure
Ce travail de Jean-Pierre Luminet montre de manière évidente que la visualisation n’est pas forcement synonyme de localisme ; elle peut envisager la description d’un type de phénomènes en se constituant en image-modèle, comme on vient de le voir avec la photographie calculée des trous noirs. Mais on voit bien aussi, par les exemples précédents, que la visualisation peut arriver à assurer une entrevision diagrammatique de différents types, à savoir un interstice entre détails et régularités (dans l’exemple de la chronophotographie du cheval) et entre enracinement de l’empreinte et modularité (dans le cas des amas de galaxies).
Photo 1