Une image ne démontre pas, elle convainc
Francis Edeline
Groupe µ - Université de Liège
Index
Mots-clés : démonstration, image, logique, mathématiques
Auteurs cités : Groupe , Colin Cherry, Francis ÉDELINE, Jean-Claude Falmagne, Gaetano Kanizsa, Jean-Marie KLINKENBERG, Alain Lieury, Valentin N. Ostrovsky, David A. Ratkowsky, Irvin Rock, Norbert Wiener, Leland Wilkinson, Pawel Zeidler
A l’issue de ces trois années consacrées, par notre groupe, à l’étude de l’image scientifique, nous devons entériner le fait qu’il existe non pas une mais des images scientifiques, de types et de fonctions diverses. Les six catégories qui me paraissent le plus nettement individualisées sont :
Figures abstraites (logico-mathématiques)
Images-sources (enregistrements visuels ou convertis en visuel)
Diagrammes conceptuels (soutiens d’un raisonnement ou d’une expérience de pensée)
Nomogrammes (sortes de machines à calculer graphiques)
Schémas
Graphiques expérimentaux ou Images de travail
- Note de bas de page 1 :
-
Voir Visible 8, sous presse.
Celle qui sans conteste a reçu de nous le maximum d’attention, c’est l’image-source. Le nomogramme par contre a été à peine mentionné, à part les quelques mots que je lui ai consacrés à Strasbourg en 20091. Si je fais cette énumération, c’est pour préciser que je m’adresserai ci-après exclusivement à l’image mathématique (un petit peu) et à l’image de travail (surtout).
1 – L’évolution intersémiotique de l’image
On se souvient que beaucoup d’auteurs, et non des moindres (Hjelmslev et Barthes !) estimaient que le langage était le système de signes le plus efficace et le plus complet, et que tous les autres systèmes, sans exception, pouvaient être traduits en termes linguistiques. Le travail de notre groupe, consacré à un corpus gigantesque d’images scientifiques visuelles, leur donne tort. La mathématique, par exemple, est à l’étroit dans le code linguistique. Paralysée par ses insuffisances, la réflexion mathématique, et plus généralement scientifique, n’a pu les surmonter que par un recours systématique à l’image. Je me propose d’examiner la principale de ces insuffisances : la séquentialité.
L’écriture des mathématiques et de la logique est devenue intersémiotique, dans le sens où elle utilise simultanément (et non conjointement comme dans les énoncés pluricodes étudiés par Klinkenberg, 2008) les mécanismes des codes linguistique et visuel.
Par exemple la simple écriture des quotients
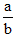
(qu’on lit a sur b) est déjà une entorse à la linéarité puisque cette disposition introduit dans l’écriture trois niveaux au lieu d’un seul. Avec
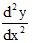
c’est cinq niveaux qui apparaissent. Par ailleurs le répertoire des signes s’est avéré lui aussi insuffisant et il est devenu courant d’utiliser dans le même énoncé des polices différentes : R , T,אַ etc. ainsi que des signes inventés comme Nabla (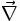 ).
).
On constate dans ces exemples une compétition entre deux forces ou objectifs : clarté de saisie pour l’esprit vs regroupement économique. On recherche le meilleur compromis, et c’est un compromis zipfien. Le regroupement est une caractéristique fondamentale du fonctionnement nerveux et de la pensée (qui procède par catégorisation et hiérarchisation).
- Note de bas de page 2 :
-
Et il y en a bien d’autres : polaire, triangulaire, elliptique, bi- ou semi-logarithmique, probit etc.
Si le langage mathématique tend à devenir intersémiotique par le recours à des dispositifs non linéaires mais spatiaux (caractéristiques des codes visuels), un mouvement inverse est notable dans l’image scientifique. Dans cette dernière en effet le langage n’est pas absent (ce qui en fait un énoncé pluricode selon Klinkenberg, 2008) mais en outre et surtout des contraintes sont introduites dans l’occupation de l’espace, qui se structure et se rapproche ainsi d’un langage selon une évolution intersémiotique. Les points expérimentaux ne peuvent se disposer n’importe où, comme dans une simple peinture, mais doivent se conformer à un formatage rigoureux dont l’exemple le plus simple est le diagramme cartésien2.
En définitive les deux systèmes vont à la rencontre l’un de l’autre : le langage devient image et l’image devient langage. Généralement dans de tels cas on parvient peu à peu et automatiquement à un état d’équilibre optimal. On se demandera alors ce qui est si précieux dans l’image, quel est le secours essentiel qu’elle apporte au langage.
En premier lieu on n’oubliera pas qu’avec l’image scientifique il ne s’agit pas d’explorer le monde par le sens de la vue. Elle n’est pas une transformation géométrique des formes visuellement perceptibles comme le seraient un portrait ou une photographie. Son rapport au monde est d’une autre sorte, comme on le verra au §3. On découvre alors que ce n’est pas la totalité des dimensions du signe visuel (forme, couleur, texture) qui est ainsi « squattée » par la pensée mathématique : seule la forme entre en ligne de compte, les deux autres ayant un rôle tout à fait secondaire. La raison en est simple : ce sont des continuums et ils concernent des surfaces, de sorte que leur capacité à porter de l’information est très limitée. C’est donc la ligne, et la forme qu’elle peut prendre, qui sont comme le verra les porteurs les plus concentrés de l’information impliquée dans une modélisation.
Le cerveau prend connaissance des énoncés via les sens, avec des limitations spécifiques à chacun d’eux. Cette question est examinée plus en détail à l’Annexe I.
Prenons le cas d’une démonstration logique ou mathématique. En termes absolus elle ne fait nullement intervenir le temps : elle est essentiellement tautologique, et sa conclusion est déjà instantanément présente dans ses prémisses. Néanmoins pour la communiquer nous aurons recours au langage qui, par son caractère linéaire, la narrativise. Joue alors la contrainte de l’épaisseur du présent, qui nous empêche de la saisir globalement si elle est quelque peu complexe. En nous aidant d’une disposition visuelle, spatiale, des étapes successives du raisonnement, nous échappons à cette contrainte grâce à la synopsie, qui nous permet de voir ensemble lesdites étapes, et est devenue de ce fait le puissant adjuvant de la pensée que nous connaissons. Deviennent disponibles simultanément le pas à pas de la démonstration et l’ensemble du processus. L’image se comporte comme une mémoire externe : on dira qu’elle dilate le présent et que, ce faisant, elle corrige partiellement l’artifice que constitue l’introduction du temps (sous la forme d’un séquençage narratif) dans la démonstration. La conviction pourra ensuite découler de la saisie globale ainsi obtenue.
Mais ceci n’est peut-être pas encore « le tout » de la conviction : cette sorte d’« éclair » par lequel une démonstration est « adoptée », prise en charge sans réserve, avec sincérité, « comme si nous l’avions trouvée nous-même », certain de pouvoir la refaire. C’est donc aussi une « participation », dont les aspects psychologiques ne me semblent pas encore clairement cernés.
2 – Les modèles
- Note de bas de page 3 :
-
Dans la suite de cette étude il s’agira toujours de modèles conceptuels, sachant qu’il existe aussi des modèles matériels , p.ex. les boules et tiges de métal utilisées pour représenter des molécules (ces derniers ont été bien étudiés notamment par Francoeur, 2000).
- Note de bas de page 4 :
-
Voir par exemple Jean-Claude Falmagne, « Mesurage, modèles mathématiques et psychophysique », Traité de psychologie expérimentale, Ed. Marc Richelle, Jean Requin, Michèle Robert, PUF, Paris, 1994 (I/3), p. 84sq.
- Note de bas de page 5 :
-
Jean-Claude Falmagne, « Mesurage, modèles mathématiques et psychophysique », Traité de psychologie expérimentale, idem, p.79.
Quittons à présent le domaine logico-mathématique pour examiner l’image de travail dans les sciences appliquées, et demandons-nous en quoi consiste exactement un modèle3. Cela nous amènera à esquisser une approche sémiotique de la mesure. En psychologie expérimentale, la théorie du mesurage reste quelque peu ambiguë4. Le mesurage consiste à « assigner un nombre » à une grandeur perçue, « en tant que mesure » de cette grandeur. La légitimité de cette assignation est garantie par l’intuition, laquelle « vient certainement de ce que notre expérience personnelle du monde physique nous a convaincus qu’il obéit à certaines contraintes ou lois ». La perception est donc clairement impliquée. Mais par ailleurs on nous avertit5 que le codage de données expérimentales dans un langage formel « appauvrit l’expérience et la concrétise. Il rend possible la construction de modèles, mais aussi en impose les limites. En effet, un modèle se définit sous la forme de propositions énoncées dans les termes de ce langage, et contraignant les protocoles expérimentaux possibles. » [je souligne]
La modélisation comporte quatre étapes successives, chacune étant génératrice d’imprécision. La fig.1 montre que deux de ces étapes se situent dans le monde physique et les deux autres dans la sphère mentale ou symbolique.
Etape (a)
Au moyen d’observations ou d’expérimentations on enregistre un corpus de points expérimentaux. On est donc passé de grandeurs physiques (des pressions, des températures, des vitesses…) à des nombres. Bien sûr la précision des moyens mis en œuvre va déjà jouer à ce stade, sans parler des relations d’incertitude qui règnent à l’échelle subatomique. Mais plus fondamentalement nous faisons par là même confiance en l’hypothèse que les propriétés des nombres (en particulier la continuité et l’existence d’une unité invariable) sont les mêmes que celles de la nature. Or si nous sommes certains que le millième euro de notre fortune a la même valeur que le premier, sommes-nous aussi convaincus qu’un degré centigrade entre 87 et 88°, dans de l’eau qui va bouillir, soit identique à un °C entre -7 et -6°, dans de la glace ?
L’ensemble de l’étape (a) va se traduire par une table de correspondance, souvent appelée légende, entre les diverses grandeurs physiques et un symbole qu’on leur aura attribué (fig.2). On est ainsi passé au plan symbolique, par la voie d’une conceptualisation : ce qui a une énorme portée au plan du réalisme, et j’y reviendrai en détail plus loin.
Etape (b)
Une fois sur le plan symbolique des nombres, on y reste pour élaborer un modèle mathématique dans lequel les symboles (et leurs valeurs numériques) sont engagés dans des relations, et dont l’état final sera une équation (fig.3). Le choix de cette équation est orienté par l’examen visuel de la disposition des points expérimentaux. Dans le cas présent (fig.4) nous rechercherons une équation pouvant engendrer une courbe, ascendante, monotone, à concavité tournée vers le bas, et asymptotique. En l’écrivant, nous faisons à nouveau confiance en des hypothèses très lourdes, qui consistent à admettre que la correspondance entre le plan symbolique et le plan réel se poursuit. En particulier :
-
qu’il existe dans le monde réel des constantes ;
-
que des propriétés telles que l’additivité (à laquelle se ramènent en somme toutes les autres opérations) y règnent aussi ;
-
qu’il existe dans la nature des lois générales ;
-
qu’il existe des lois de conservation (de la masse, de l’énergie, de la quantité de mouvement… peu importe) que l’on pourra manifester par le signe =, caractéristique de toute équation (un illuminé créationniste n’a pas le droit d’écrire une équation).
Cette étape n’entraîne comme erreurs que celles liées à l’oubli de facteurs actifs ou à des hypothèses simplificatrices.
Etape (c)
Cette étape consiste à calculer des valeurs théoriques à l’aide du modèle, et donc entraîne des erreurs d’arrondi dans le calcul du résultat final. Ensuite on visualise ces résultats par des tracés graphiques, qui sont exécutés avec des instruments imparfaits, donnant des traits ayant une épaisseur, des points non ponctuels et des angles approximatifs. On produit ainsi une image de travail où figurent simultanément les points expérimentaux provenant du monde naturel et les valeurs calculées issues du modèle conceptuel (fig.4). C’est donc une surface de contact entre le sujet et l’objet. Elle opère un retour au monde physique.
Etape (d)
Il reste à comparer les valeurs observées aux valeurs calculées. C’est ici que la puissance de conviction du canal visuel se manifeste à plein, car un tableau de chiffres n’a guère le même pouvoir. Le degré de correspondance entre les deux séries de valeurs est apprécié visuellement d’abord, puis calculé à partir de leurs écarts ε. Une partie des écarts provient des imperfections et erreurs relevées plus haut (… et qui ne se compensent pas nécessairement, comme on aimerait à le croire !), et le reste est dû à l’imperfection du modèle lui-même. Idéalement ε ne doit pouvoir être corrélé à rien. L’analyse de l’erreur revêt donc une importance cruciale, sur laquelle je reviendrai plus longuement, exemples à l’appui. On observera enfin que l’ensemble des quatre étapes forme un cycle fermé, et même une boucle, fait sur lequel je reviendrai également.
- Note de bas de page 6 :
-
Les chercheurs européens ont tendance à privilégier l’approche hypothético-déductive (ils cherchent avant tout à comprendre), alors que l’approche anglo-saxonne est plus volontiers empirique (on renonce à comprendre, voire on estime qu’il est vain d’essayer de comprendre, et on se satisfait de décrire).
Devant un ensemble de données expérimentales, un grand nombre de modèles sont concevables. On peut les diviser en deux grandes classes : les modèles rationnels ou hypothético-déductifs, et les modèles empiriques ou descriptifs. De nombreux modèles se situent toutefois entre les deux : partis d’une formulation rationnelle stricte, ils ont ensuite amélioré leurs performances par l’introduction de paramètres correcteurs empiriques6.
Un modèle est dit « théorique » lorsqu’il s’inscrit dans le cadre d’une théorie générale préexistante. Un tel modèle doit avoir une valeur explicative et non simplement descriptive. Être explicatif signifie (a) avoir identifié tous les facteurs en jeu (ou au moins les principaux), et (b) proposer entre eux des relations quantitatives validées par l’expérience. Un modèle simplement descriptif, plus souvent appelé empirique, peut se révéler très supérieur dans sa correspondance avec les faits observés, mais il ne possède aucune valeur explicative. Lorsqu’on a établi d’un processus un modèle empirique, même extrêmement satisfaisant sur le plan descriptif et même prédictif, on ne peut aucunement prétendre en avoir trouvé le sens.
Il est piquant d’illustrer ce point à partir justement des théories de la perception, en particulier visuelle, où se rencontre précisément la compétition entre les deux approches (v. fig.5). Le modèle de Weber-Fechner est un bon exemple d’approche hypothético-déductive à haute valeur explicative mais à pouvoir de prévision limité. Le modèle semi-empirique de Stevens par contre est dénué de valeur explicative : l’exposant p qu’il contient n’a aucune signification bio-physique, et de plus il rend l’équation fortement non-linéaire, mais son équation « colle » mieux aux faits.
Une autre faiblesse constitutive des modèles empiriques est qu’ils ne fonctionnent qu’entre les limites des valeurs observées ayant servi à les établir : ils ne peuvent être extrapolés, alors que les modèles hypothético-déductifs le peuvent. Illustrons ce point par un exemple. On a calculé que la distribution diurne de la concentration des eaux d’égout de la ville de Minneapolis (en 1971) pouvait être normalisée en y ajustant un polynôme du 4° degré, pour tenir compte des pics et des creux observés dans l’évacuation (2 max. et 2 min.). La concordance est excellente, mais le modèle ne peut évidemment être utilisé pour des prévisions, car dans la réalité le cycle se reproduit chaque jour alors que le modèle n’est pas cyclique.
On voit à quel point le sens de la vue est impliqué dans ces procédures, même si le dernier mot appartient toujours au calcul.
3 - Le réalisme
- Note de bas de page 7 :
-
Colin Cherry, On human communication. New York, Science editions, John Wiley, 1961, p. 62.
Dans le travail scientifique on est toujours pris en tenaille entre deux souhaits quasi-antithétiques : le souhait rationnel de comprendre ce qui se passe dans la nature, et le souhait pragmatique de la prévoir avec précision afin d’agir sur elle avec efficacité. Le premier souhait conduit nécessairement à une simplification, donc à une description approximative du réel. En outre cette compréhension a son siège dans la sphère mentale, où elle prend une forme symbolique et s’exprime par des concepts : or le symbole est par définition distinct de la chose signifiée, et le concept n’est pas un objet de la nature (en d’autres termes : la nature ne fonctionne pas à coup de concepts).C’est ce qui a conduit beaucoup de philosophes des sciences à nier qu’un modèle ait une quelconque ressemblance avec les phénomènes qu’il prétend décrire. Ce débat épistémologique sur le statut ontologique des modèles est crucial, mais ce n’est pas ici le lieu de l’aborder, sinon pour préciser que nous ne pouvons accepter ni le réalisme inconditionnel ni l’antiréalisme radical et penchons pour une solution interactive, dont précisément l’« image de travail » est la parfaite illustration. Nous adhérons donc, en tant que sémioticiens cognitivistes et interactionnistes, parmi toutes les formes de réalisme énumérées par Petitot et d’autres (fig.6), à un réalisme modéré. Avec Colin Cherry7 nous pensons que la nature n’est pas intrinsèquement signifiante. Nous en recevons des signaux et non des signes. La nature « ne coopère pas », car « il n’y a pas de lien de type communicationnel avec le monde naturel ».
Certains aspects de l’option choisie quant au réalisme ne peuvent néanmoins être passés sous silence, car ils ont une incidence directe sur la façon de concevoir et de traiter les modèles. Trois cas me paraissent se dégager, et on voit immédiatement que le type d’équation susceptible de modéliser chacune de ces options est fondamentalement différent :
- Note de bas de page 8 :
-
Norbert Wiener, Cybernétique et société - l'usage humain des êtres humains, Paris, 10/18, 1962, p. 10.
-
Option déterministe
-
Forme classique : Natura non facit saltus.
-
Formes actuelles : pour Thom c’est le contraire, nous ne percevons que des discontinuités ;
selon la théorie du chaos, une sensibilité extrême aux conditions initiales, conjuguée à l’impossibilité pour nous de les mesurer avec une précision absolue, conduit à des états en apparence chaotiques mais néanmoins strictement déterminés.
-
-
Option indéterministe
pour Wiener8: « le hasard est non seulement (…) un instrument mathématique au service de la physique, mais (…) une partie de la trame et de la nature de la Nature. »
- Note de bas de page 9 :
-
Norbert Wiener, Cybernétique et société - l'usage humain des êtres humains, idem, p. 7.
- Note de bas de page 10 :
-
Et les relations d’incertitude le confirment quantitativement.
Contrairement à l’opinion de Norbert Wiener, qui reconnaît d’ailleurs lui-même qu’« aucune mesure physique n’est parfaitement précise»9, c’est dans le concept même de mesure, c’est-à-dire à la faveur de cette opération par laquelle nous pensons pouvoir attribuer (sans perte) des grandeurs du monde physique à des nombres du domaine mathématique, que s’introduit en partie le flou que nous appelons hasard. C’est donc bien de nous, de notre intervention, qu’il procède10, et cela ne démontre nullement que le hasard soit un constituant du réel, constituant dont on serait d’ailleurs bien en peine de définir la nature. Que ce flou ait une structure, et qu’il obéisse à la loi dite « des grands nombres », reste néanmoins mystérieux…
4 – Pour un réalisme indiciel.
- Note de bas de page 11 :
-
Edeline, Visible 8, Actes des journées d’étude de Strasbourg, 2008, sous presse.
Il est tout de même remarquable qu’une science efficace ait pu se développer sous des bannières aussi différentes. Cela suggère que ces options ne concernent que le cadre conceptuel de notre travail, le réel lui-même ne pouvant être abordé qu’indirectement et de façon eidétique. Mais on ne peut pour autant dénier aux modèles, et donc aux images qu’on en tire, toute capacité de représentation isomorphique ou homéomorphique. En effet dans la chaîne qui va d’un processus physique aux points expérimentaux que nous en recueillons, puis à leur transposition symbolique et au travail de modélisation, quelque chose se conserve qui est de l’ordre de la forme. Qu’il en est bien ainsi est démontré par le chemin inverse, qui nous assure une prise non illusoire sur les choses. L’ensemble de ces opérations n’est autre qu’une sémiose, avec ses deux volets, ana- et cata-sémiotique11.
- Note de bas de page 12 :
-
Ceci a lieu à l’échelle micro, où jouent les relations d’incertitude, en particulier lorsqu’on cherche à représenter la forme, la structure, la configuration d’une molécule. Cette restriction n’est toutefois plus d’application lorsqu’on détermine des grandeurs à l’échelle macroscopique. Pawel Zeidler, "The Epistemological Status of Theoretical Models of Molecular Structure" HYLE.6 n°1, 2000, p. 8.
- Note de bas de page 13 :
-
Pawel Zeidler, "The Epistemological Status of Theoretical Models of Molecular Structure", idem, p. 9.
- Note de bas de page 14 :
-
Ramsey, apud Zeidler, idem, p.10
Pourtant dans le débat sur le réalisme on invoque le fait que la technique de mesure modifie l’objet mesuré12. On en déduit par exemple qu’une molécule n’a pas de forme « en soi » et permanente : la forme est une propriété momentanée13, elle n’est pas une propriété intrinsèque mais une propriété de réponse14. De là on en vient à nier qu’un modèle élaboré sur de telles bases puisse présenter la moindre similitude structurelle avec l’objet modélisé. Les modèles sont alors vus comme de simples constructions, c’est-à-dire, sous-entendu, arbitraires.
- Note de bas de page 15 :
-
Le monde vivant nous offre quelques exemples remarquables de cette identification/copie par empreinte, sanctionnés par l’évolution. La spécificité enzymatique (qui peut aller d’une classe entière de réactions chimiques à celle d’un isomère optique) est expliquée par la configuration stérique de l’enzyme par rapport à son substrat. Les phénomènes de rejet dans le système immunitaire s’expliquent de façon semblable, tout comme l’action des cellules réceptrices du goût dans la théorie d’Amoore (1952). Quant à la double hélice, elle n’engendre pas une copie allant du même au même, mais bien la création d’un véritable négatif au moyen des bases puriques conjuguées. La répétition de cette opération, soit la création du négatif du négatif, réalise alors la copie exacte.
Pour résoudre cette difficulté des positions réalistes, il convient selon moi de considérer l’ensemble « système mesuré – système mesurant ». Ils sont en interaction. S’il est vrai que le second influence le premier, il est tout aussi vrai que le premier influence le second : c’est ce qui nous fournit les « points expérimentaux ». La nature de cette influence est à creuser car c’est en elle que réside la similitude niée par certains. Le mot similitude est d’ailleurs sans doute ici trop fort. Il serait plus productif d’aborder le problème à partir du concept d’indice et d’élaborer un réalisme indiciel : l’empreinte, le symbolon, sont des images en creux, en négatif, mais elles sont suffisamment fidèles pour permettre la reconnaissance15. Dans le cas qui nous (pré)occupe existe aussi cette continuité matérielle (par contact, ou mieux interaction) qui définit sémiotiquement l’indice.
On peut donc admettre que l’« empreinte » obtenue par une technique expérimentale déterminée est fidèle « dans les conditions de la mesure ». D’accord elle ne donne pas l’image absolue et éternelle d’un objet,- qui n’est d’ailleurs ni absolu ni éternel mais en incessante interaction,- mais elle est quand même exacte hic et nunc et sic.
- Note de bas de page 16 :
-
On laissera de côté, parce que non pertinent ici, le problème du réalisme abordé plus haut.
Jimenez (1997) évoque le cas d’un individu qui se déplace à tâtons dans le noir et dans un environnement qu’il ne connaît pas : « Il ne perçoit, stricto sensu, que l’aire couverte par ses pieds ou ses mains (…) S’il se heurte à un obstacle, il saura quelque chose à propos de ce que son environnement n’est pas, sans pourtant mieux connaître ce qu’il est. » Nous interpréterions différemment cette expérience de pensée. L’individu en question a bel et bien obtenu une information indicielle (puisqu’il y a eu contact physique) sur son environnement, et c’est le maximum qu’un être percevant puisse espérer.16 Ce que montre cet exemple extrême, c’est que les informations perceptives recueillies (ici tactiles mais il en va de même pour les autres sensorialités) peuvent n’être pas jointives (les deux mains et les deux pieds sont séparés) et néanmoins permettre au sujet de résoudre son problème de traversée. Dans le cas d’un être humain normalement constitué, ce recueil d’informations a beau être énormément renforcé par l’existence de sensorialités multiples et performantes, il demeure néanmoins parcellaire. Nous « palpons » le monde et construisons de lui une image partielle en creux qui est strictement de l’ordre de l’indice. Le reste n’est que reconstruction inférentielle. A y regarder de près, nous ne percevons jamais que le négatif des choses, puisque nous sommes par rapport à elles toujours en dehors. C’est par un travail de reconstruction mentale que nous les établissons dans le statut d’objet.
Il semble également qu’on puisse faire un parallèle entre
(1) le dispositif expérimental, où coexistent le système mesuré et le système mesurant ;
(2) l’image de travail, où coexistent des points expérimentaux et un modèle.
Dans les deux cas on observe l’affrontement sujet/objet, qui est bien le point origine de toute sémiotique, et à partir duquel on peut remonter à l’opposition suivante :
(1) au plan des concepts ou des symboles règne le mode Σ ;
- Note de bas de page 17 :
-
Sur le sens de ces deux notions, voir Groupe µ (1970).
(2) au plan des objets règne le mode Π17.
A cela tiendrait l’impossibilité d’atteindre une coïncidence parfaite entre la pensée (subjective) et l’univers (objectif). La pensée est faite de concepts, par définition généraux et immatériels, alors que l’univers est fait de particules individuelles et matérielles (avec les corrections que la physique actuelle impose au mot matière) qui interagissent. Nous disons « hydrogène » ou « électron », mais qui nous assure que tous les neutrons ne diffèrent pas les uns des autres (comme les visages des hommes ou les feuilles des arbres) par des traits non encore aperçus ? Le mode Σ confère à ces êtres finis que nous sommes des concepts de portée infinie : c’est sans doute la seule possibilité pour nous de saisir un monde qui est infini dans sa nature.
5 - Les pièges de la représentation visuelle
On commencera par souligner la grande différence qui distingue l’image mathématique de l’image de travail : c’est que dans la première la fiabilité du sens de la vue joue un rôle quasi nul. Il est parfaitement possible de faire un raisonnement juste sur une figure fausse ou grossièrement approximative. La raison en est simple : ces figures ne contiennent que des concepts et ne sont aucunement en relation avec le monde des objets. Ce qui suit concernera donc exclusivement les images de travail.
- Note de bas de page 18 :
-
Dont les quatre plus connues sont : la réciproque, l’exponentielle, la logarithmique et la fonction puissance.
Ce qui vient d’abord à l’esprit lorsqu’on parle de pièges visuels, c’est l’ensemble des illusions d’optique et des phénomènes de construction d’images par l’appareil visuel. Ils ont été abondamment étudiés par les psychologues de la Gestalt et par leurs continuateurs comme Kanizsa (1997) ou Rock (2001). Il est inutile d’insister sur ces phénomènes bien connus et même largement popularisés (fig.7). Ceci étant dit, l’image de travail essaie de profiter au maximum de la grande sensibilité de l’œil à la rectilinéarité. Un écart à la ligne droite est aisément perçu, alors que le même œil ne permet guère de distinguer entre eux des arcs de cercle, d’ellipse, d’hyperbole, d’exponentielle etc. C’est pourquoi si une équation se représente par une courbe, on cherche d’abord à la linéariser par diverses transformations algébriques18. Mais ce faisant on introduit une anamorphose qui peut se révéler trompeuse, notamment en contractant les écarts dans certaines zones et en les dilatant dans d’autres. C’est surtout pour une inclinaison proche de 45° que l’œil excelle à juger de la rectilinéarité. La fig.8, reproduite de Wilkinson (2000), montre en outre qu’en jouant sur les échelles on peut renforcer ou atténuer l’impression de corrélation.
Moins connus et bien plus pernicieux sont les problèmes statistiques associés à l’ajustement graphique d’un tracé théorique, issu d’un modèle, à des points expérimentaux issus du monde naturel. J’en soulignerai trois, d’après Ratkowsky (1990).
Le premier concerne le coefficient de corrélation R2, dont on croit souvent qu’il donne dans tous les cas le « % de variation expliquée » par le modèle. On s’en sert donc pour apprécier le « fit », ou qualité de l’ajustement. En fait ce n’est strictement vrai que pour des modèles linéaires ayant un terme constant. Si ce n’est pas le cas il faut examiner la structure de l’erreur résiduelle et entrer dans une procédure compliquée où R2 n’a plus aucun rôle à jouer. Mais il existe heureusement des compromis acceptables : les modèles quasi-linéaires, dont le nom indique bien qu’ils sont des approximations.
Les deux autres problèmes sont de loin plus graves, car ils engagent le statut épistémologique des modèles. Un modèle est par essence général. Fait de concepts, il doit s’appliquer à de multiples situations et non à une seule. Sa généralité est garante de son pouvoir explicatif, dont découlent aussi ces phénomènes d’ordre intuitif et fort mal connus : la compréhension et la conviction. Mais la recherche de la généralité entraîne automatiquement une perte dans la qualité de la prévision : ces deux types de qualité varient en sens inverse l’une de l’autre. On illustre bien cette antinomie par l’inférence bayesienne (du nom du génial statisticien Bayes). La fig.9 montre que le modèle M1 prévoit avec grande précision les données comprises dans la fourchette C. Le modèle M2 est beaucoup moins précis dans ce domaine, mais il étend par contre ses prévisions à un domaine bien plus large que C.
Nous avons déjà rencontré cela avec les équations de Fechner et de Stevens, où les points expérimentaux se disposent selon une courbe dont la concavité est tournée vers le bas. Le modèle de Weber-Fechner est simple et linéaire au sens mathématique du terme, par contre le modèle de Stevens est rendu fortement non-linéaire par le paramètre p en exposant. Il s’ensuit que dans ce dernier modèle le coefficient R2 de régression ne représente pas le % de variabilité expliquée, même si (pour l’œil comme pour le calcul !) l’ajustement semble meilleur.
Réexaminons cette question en termes statistiques. Un modèle tel que M1 est généralement plus compliqué et comporte davantage de paramètres. Or, ajouter des paramètres diminue le nombre de degrés de liberté et fait par conséquent augmenter la variance, de même que la non-linéarité. C’est surtout grave lorsque des paramètres nouveaux apparaissent en exposant. La recherche de modèles compliqués est contraire au principe de parcimonie (Occam fut excommunié !). A la limite on peut faire passer la courbe du modèle par tous les points expérimentaux : il suffit que le nombre de paramètres soit ≥ au nombre de points. Mais alors la plupart des paramètres ne sont plus mesurables ou n’ont pas de signification physique. C’est le cas de l’excellente équation de Benson & Krause permettant de calculer la quantité d’oxygène que l’on peut dissoudre dans l’eau à n’importe quelle température (fig.10).
On a donc, pour des raisons statistiques, intérêt à rechercher un modèle de forme simple et comportant un nombre minimum de paramètres. Mais pas un modèle trop simple, qui se contenterait par exemple de modéliser une croissance ou une décroissance sans s’inquiéter de sa forme, alors que le phénomène est notoirement plus complexe : un tel modèle n’explique plus rien, car il peut servir partout et est trop général.
En résumé, deux pièges sont à éviter : la surparamétrisation et l’excès de généralité.
6 - Une philosophie de l’approximation
Après avoir montré tant d’exemples de données expérimentales « dispersées », je n’aurai aucune peine à enchaîner avec le problème de l’approximation en science. La grande question est de savoir si le comportement erratique des systèmes physiques est inhérent au monde physique ou simplement dû à l’imperfection de nos mesures, ou les deux. Notre position sur le hasard a déjà été précisée plus haut. En fait nous posons à la nature des questions trop simples, et c’est pourquoi elle nous répond imparfaitement. Toute expérimentation est la traduction de notre intention d’obtenir la réponse à une question déterminée, mais elle relègue de ce fait tous les autres fils de l’écheveau au rang de bruits.
- Note de bas de page 19 :
-
Quelques exemples d’approximations assumées : le mouvement sans frottement, le fluide sans viscosité, la masse de l’électron supposée nulle.
- Note de bas de page 20 :
-
Un cas parmi des centaines d’autres : le repérage de raies noires dans le spectre des rayons solaires, que l’on avait d’abord cru continu.
Celui qui se consacre aux sciences de la nature doit apprendre à vivre dans l’approximation19. Il doit en comprendre l’origine (les origines). Au lieu de la déplorer et de la considérer comme un mal nécessaire, il doit reconnaître en elle (sans paradoxe !) l’unique source de progrès. En effet l’approximation est un écart par rapport à un modèle, et un écart est toujours source de sens. Le cycle dont il a été question plus haut (fig.1) est en réalité une boucle, par laquelle se met en place un va-et-vient heuristique. Or c’est d’abord sur l’image que sont détectés les écarts, dont l’existence nous rappelle l’imperfection de tout modèle. La science progresse exclusivement par la détection et l’analyse de ces écarts. Ce qui est bruit aujourd’hui sera source d’information demain. Il y a de cela d’innombrables exemples20. Une telle attitude est exactement l’inverse de la résignation devant la fatalité du hasard, que suppose la position de Wiener. Ainsi l’image scientifique nous informe aussi bien positivement que négativement.
Les fig.11 et 12 montrent comment, poursuivant notre exemple, nous pouvons extraire d’une analyse de la structure de l’erreur résiduelle (écarts entre valeurs observées et valeurs calculées) deux informations intéressantes : (1) cette erreur n’est pas indépendante mais bien liée à la pente de la courbe, et (2) les valeurs observées finales sont systématiquement inférieures aux valeurs calculées, ce qui fait présumer une erreur par défaut sur Cs.
Cette idée d’une progression de la science grâce à des approximations successives implique aussi celle que ces approximations sont chaque fois meilleures (d’où le progrès). Les écarts avec l’observation ne peuvent que diminuer, sinon la nouvelle théorie qui les produit serait rejetée. D’où la notion d’un processus asymptotique, ou d’une convergence, avec un horizon peut-être impossible à atteindre mais à l’existence duquel on affecte de croire : le modèle de Dieu le Père, avec ε = 0. C’est un réalisme asymptotique.
La thèse de l’approximation en science a été traitée de façon provocante par Valentin Ostrovsky (2005). Il suggère une complémentarité entre sujet et objet dans le statut même de la science, vue comme une interface entre les deux. Il oppose ainsi le quantitatif (recherche de solutions objectives exactes) au qualitatif, basé sur des approximations à grande valeur heuristique et pouvant servir de support à l’intuition. Il incite à étudier de plus près le mode dit qualitatif, nécessairement lié à un sujet, tout comme l’est aussi le sens, par opposition à l’information liée, elle, au quantitatif. Il va jusqu’à proposer la fusion des deux concepts : le sens c’est la qualité. Mais ce concept de qualité reste bien difficile à définir avec précision. Dans une envolée finale, Ostrovsky place cette distinction sous l’autorité du Principe de Complémentarité de Bohr, généralisé.
7 – Quelques conclusions
On voit qu’en science une image n’intervient jamais seule : elle fait partie d’une procédure dont elle n’est qu’un moment, d’une chaîne dont elle n’est qu’un maillon. Mais c’est une procédure cyclique et ce maillon est déterminant, car c’est lui qui permet la synopsie, c’est-à-dire qui dilate le présent.
- Note de bas de page 21 :
-
Parmi les exemples les plus connus : l’analogie hydraulique en électricité.
Sur le plan formel, son évolution intersémiotique la fait participer directement à la démarche rationnelle. En permettant, même à ce qui n’est pas visuel, de transiter par le visuel (des intensités, des potentiels, des viscosités, des vitesses, des pressions, le temps…) son rôle dépasse l’iconisme étroit d’un portrait mais se situe davantage au niveau du concept mental. Elle est d’ailleurs par excellence le lieu de l’interface sujet/objet, interface qui affecte la forme d’une liaison indicielle. Elle oblige ainsi à s’interroger sur le concept de forme puisqu’elle permet de repérer une communauté de forme entre des phénomènes par ailleurs très dissemblables21. Le degré ultime de cette conceptualisation formelle est la mathématique qui est, selon la belle formule de Valéry, la « physique de l’objet quelconque ». Ayons donc un instant de recueillement à la mémoire de l’évêque Nicole Oresme, inventeur de la représentation graphique au XIV° Siècle.
Annexe I Avantages comparés du visuel et du linguistique.
Ce point mérite d’être examiné en profondeur et en s’appuyant sur des données techniques. Le flux d’information émanant des divers sens humains se caractérise par une capacité très variable. L’ouïe et la vue figurent en première place et cette dernière est créditée d’une capacité sept fois supérieure à la première. En outre l’oreille fournit un flux nécessairement séquentiel, alors que l’œil peut travailler selon la linéarité du code linguistique aussi bien que selon la spatialité des codes visuels. A cela s’ajoute la spécialisation hémisphérique du cerveau : chez les droitiers le langage est exclusivement traité par l’hémisphère gauche (aire de Broca), alors que l’image peut être traitée par les deux hémisphères et peut ainsi tirer avantage du « traitement parallèle ».
- Note de bas de page 22 :
-
Je retiens les chiffres donnés par Herbert Franke (1974), plus récents et plus précis que ceux de Moles, qui donnait la fourchette 60 à 200 bits.
On peut tenter de chiffrer ces différences . Le premier élément à prendre en compte est l’épaisseur du présent (expression semble-t-il introduite par Abraham Moles en 1958). Le présent psychologique n’est pas un instant sans durée mais est caractérisé par une mémoire spéciale à court terme (la Conscience ou Kurzspeicher) acceptant un flux d’information de 16 bit/s et assurant leur rétention pendant 10 s, après quoi il y a effacement, ou transfert dans un autre niveau de mémoire, l’Attention (ou Gedächtnis). Deux évènements sensoriels séparés par moins de 1/16° de seconde sont inexorablement fusionnés (ce qui explique la limite de l’oreille dans les sons graves). On voit que le contenu de la mémoire immédiate est de l’ordre de 16 bit/s x 10s = 160 bits22.
L’attention mémorise les informations pour une durée beaucoup plus longue, et se caractérise par un effacement selon une exponentielle décroissante. Par contre elle accepte seulement un débit d’information de 0,7 bit/s, soit environ le trentième de la mémoire immédiate. Tous calculs faits cette mémoire dispose d’une capacité de rétention de ± 106 bits.
Il n’échappera à personne qu’il s’agit là d’une combinaison de valeurs rendues optimales par l’évolution, mais qui ne sont plus nécessairement optimales au regard des situations auxquelles est confronté un humain d’aujourd’hui. De toute manière un système mémoriel ne peut fonctionner que s’il comporte un mécanisme d’effacement ou d’oubli.
- Note de bas de page 23 :
-
Voir notamment Alain Lieury, Psychologie cognitive, Paris, Dunod, 2008
Est-il possible de comparer les valeurs assez précises attribuées au système séquentiel à celles qui caractérisent le système spatial ? Les études23 concernant l’utilisation séquentielle du système visuel (donc pour la lecture) sont assez avancées. Elles précisent que l’œil alterne des fixations de ± 250 ms avec des saccades de 20 à 80 ms. Au cours des 10 s du présent, on aurait ainsi ± 30 fixations. Si lors de chaque fixation on peut saisir un mot de 4 lettres, nous admettrons qu’on peut saisir 25 mots d’une longueur quelconque pendant l’épaisseur du présent.
On peut alors hasarder une traduction en bits de ces performances. Les signes alphabétiques sont identifiés parmi un répertoire de 26 lettres plus quelques autres signes. Admettons un total de 32 pour avoir une puissance de deux : 32 = 25. Un signe identifié nécessite 5 choix binaires, soit 5 bits. On a donc 4 signes = 20 bits à chaque fixation, et 30 fixations en 10 s donnent alors 600 bits.
Mais le rythme du cadençage n’est pas limité à la lecture, il vaut aussi pour l’exploration spatiale d’une image. Le champ fovéal permettant une vision nette est un angle solide de 2°. A l’intérieur de ce champ l’œil peut discriminer deux points s’ils sont séparés par 1 minute d’angle au minimum, déterminant une sorte de cellule minimale ou pixel. On calcule facilement qu’un champ circulaire de 2° comporte 11.300 de ces cellules. Nous avons précisé que dans l’image scientifique (graphiques, schémas, images de travail, diagrammes conceptuels…) on ne retient le plus souvent que la forme, au mépris de la couleur et de la texture, et ce de façon discrétisée en Noir & Blanc. Chaque pixel apporte alors 1 bit d’information. En admettant que le champ fovéal soit complètement exploré au cours d’une fixation, et que les champs successifs ne se recouvrent pas, on arrive, en 10 s et par 30 fixations, à un total de ± 340.000 bits, soit près de 600 fois plus qu’en lecture.
C’est dans ce sens qu’on pourra dire, après ce calcul sommaire, que l’image dilate le présent. En outre, comme elle demeure présente devant les yeux sans s’effacer, elle constitue une mémoire externe qui renforce la mémoire immédiate et permet à l’attention d’emmagasiner les informations à son rythme. Les 340.000 bits restent en effet inférieurs aux 106 bits de cette dernière. Le risque d’overflow est ainsi considérablement diminué voire écarté.
La comparaison des nombres (600 vs 340.000) doit cependant être relativisée, car la lecture alphanumérique est directement digitale et se raccorde aisément à l’univers sémantique, alors que l’image est à peu près strictement analogique (la réserve porte sur son caractère intersémiotique, abordé plus haut) et doit donc encore être interprétée. L’utilisation de plus en plus universelle de l’image témoigne néanmoins éloquemment de ses avantages.