L'image scientifique comme lieu de travail
Il ne faut pas oublier qu’avant de revêtir sa forme définitive et d’être imprimée dans un rapport ou dans une publication, l’image scientifique a été le lieu d’une élaboration complexe, qui fait partie intégrante des procédures de la découverte scientifique. Partant des données expérimentales brutes, elle met en œuvre, par tâtonnements le plus souvent, diverses stratégies visant à faire apparaître de façon probante des faits significatifs immergés dans ces données. On peut même considérer que c’est justement cette élaboration qui confère aux données une signification, et ce avant qu’aucun texte n’ait été écrit. Seul le dernier état de ces tâtonnements est livré au public.
One must never forget that before taking its final form, and being printed in a report or a scientific journal, the scientific graph has been the object of a complex elaboration, which is an integral part of the scientific discovery processes. Starting from the raw experimental data, it deploys, mostly by trial and error, sundry strategies in order to render apparent, in a conclusive way, some significant facts immerged in these data. One may even consider that it is through that very elaboration that the data acquire a meaning, and this before any text has been written. Only the last stage of the trials is released to the public.
Je compte aborder l'image scientifique en me prévalant de ma carrière de chercheur, c’est-à-dire en partant d'un point de vue différent de celui qui découvre ces images toutes faites, au détour d'une revue ou d'un livre, ou en assistant à une conférence. Pour celui-ci l'image est un objet comme un autre, qu'on peut collectionner, décortiquer, classer, évaluer. Au contraire il s'agira ici de l'examiner in statu nascendi, en détaillant certaines des procédures utilisées pour la construire, et en les situant sur le plan épistémologique, à partir notamment des idées de Piaget et de Fisher.
Je m’adresserai particulièrement aux images construites par points, par un scientifique, dans un espace de travail choisi librement, par opposition aux images-sources, qui constituent un matériel d’origine expérimentale pouvant être retraité, simulé et modélisé en conservant son espace d’origine. Les images-sources ont fait l’objet déjà de maintes études approfondies (Allamel-Raffin, 2006).
1. Le schéma piagétien
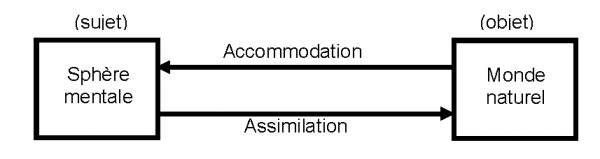
L'image scientifique est un maillon essentiel de la plupart des démarches cognitives d'aujourd'hui. Si on considère celles-ci comme une mise en rapport de la sphère mentale avec le monde naturel, c’est-à-dire comme l’établissement d’un rapport symbolique avec ce dernier, on peut utilement leur appliquer le schéma piagétien assimilation / accommodation.
Fig. 1a : Le schéma piagétien
La fig.1a rappelle que les modèles mentaux que nous formons de la réalité ne sont jamais parfaits mais sont les moments temporaires d’une suite infinie de mouvements alternés : par l’assimilation nos modèles proposent une vision schématisée et hypothétique du monde naturel, mais si l'écart entre les deux est trop grand, si la déformation est exagérée, les données issues du monde naturel vont nous contraindre à accommoder notre modèle. C'est bien ces processus que désignent les expressions familières : « approximations successives » ou « trial and error ».
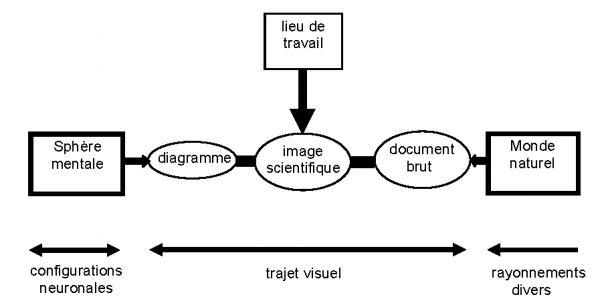
Fig.1b : Place de l’image scientifique
- Note de bas de page 1 :
-
... mais l'un se ramène à l'autre, cf. Edeline, 2008.
On peut alors préciser ce double mouvement à l'aide de la fig.1b, valable pour les cas (très nombreux) où une partie du processus cognitif fait intervenir la vision. Dans ce schéma le diagramme conceptuel (par exemple fig.2), qui schématise un raisonnement interprétatif, fait clairement partie du mouvement d'assimilation. Il est situé au plus près de la sphère mentale. Par contre le document brut (par ex. fig.3, un tableau de chiffres ou une image enregistrée1) est ce qui va déclencher une accommodation. De tels documents sont certes issus de la sensation, mais il ne faut pas oublier que la perception qui les regroupe est déjà influencée par les structures logico-mathématiques : c’est en effet celles-ci qui conditionnent notre manière de concevoir nos expériences. Le document brut dépend déjà de la façon dont la question a été posée, ce qui fait écrire à Vorobeïtchik (1969) : « Les lois que découvre le savant ne sont pas des lois intrinsèques de la nature, mais des lois qui dépendent de la manière dont le savant interroge la nature ».
Fig. 2 : Un exemple de diagramme conceptuel (Claude Zilberberg)
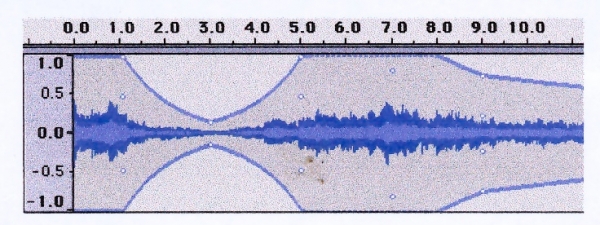
Fig. 3 : Un exemple de documents bruts : enregistrements sonores et leurs courbes enveloppes
Par ailleurs les organes des sens sont autant de filtres qui, tout en les simplifiant, mettent déjà en forme les stimuli reçus du monde extérieur. Comme l’écrit Cléro (2000 :29) reprenant les thèses bien connues de Goodman (1976) :» Les mythes de l’œil innocent et du donné absolu sont de fieffés complices. » Le document brut n’est brut que dans la mesure où il est situé au plus près du monde naturel. Il existe donc des modèles inscrits dans notre système nerveux périphérique, et il est intéressant de comparer le mécanisme de mutation-sélection, par lequel s’enregistra cette inscription, avec le schéma piagétien d’assimilation-accommodation. Le premier est une démarche consciente et délibérée, alors que le second est un processus aveugle. Néanmoins ils comportent tous deux deux étapes, et conduisent tous deux à une adaptation toujours meilleure.
Le contact entre les deux sources et leur mise en conformité (espérée) sous la forme d'un modèle s'opère dans un troisième lieu, un lieu de travail qui n'est autre que le type d’image scientifique ici envisagé. Il ne s'agit pas encore de l'image précise, claire et convaincante, qui terminera sa vie dans un article ou dans un traité, mais de l'ensemble des tâtonnements, des essais manqués, des erreurs de tout genre, des hypothèses abandonnées, de tous les brouillons et épures qui témoignent visuellement du travail de mise en conformité. Bref, c'est l'image scientifique en train de se faire, et la démarcation entre les trois types de documents n'est pas toujours parfaitement nette.
Il s’agit d'un travail sur des signes, qui s'effectue à l'interface entre le monde mental et le monde naturel, et qui de ce fait constitue un des lieux où se joue l'équilibrage interminable, parce que toujours remis en cause, entre assimilation et accommodation. Il consiste en actions sur des symboles selon un processus parallèle à celui que Piaget décrit sur des objets. La coordination des actions sur le réel, qui selon Piaget est seule génératrice de connaissance, permet le passage de la perception à la notion. Le fait que nous puissions agir aussi sur des symboles consacre l'intérêt, souvent vital, des systèmes sémiotiques. On reviendra sur ce point en 5. C’est l’ensemble de cette démarche que vise C. Allamel-Raffin (2006) lorsqu’elle écrit que les images « ne sont ni des données brutes de l’expérience, ni de simples fictions, elles permettent un type de médiation particulier avec le réel, » et c’est l’analyse de cette médiation qui constitue le sujet du présent travail.
Car que fait-on exactement dans cet atelier ? Typiquement l’image comporte un espace et des points.
2. L'espace
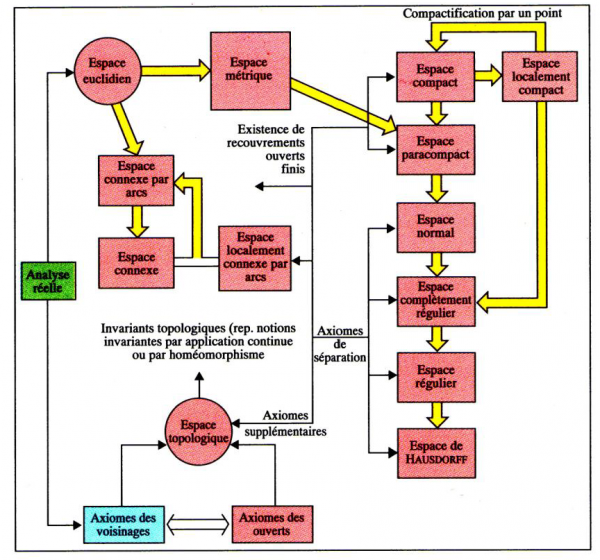
Pour un mathématicien, un espace est un ensemble structuré de points. Suivant la structure en question on peut définir de nombreux types d'espaces, et la fig.4 donne un aperçu de leur variété. Ce sont des espaces conceptuels et il importe de bien les distinguer des espaces perceptifs. Notre champ visuel par exemple est un espace perceptif dont Piaget (à la suite des expérimentateurs de la Gestalt) a bien souligné qu'il était irrégulier dans les marges et ne pouvait être considéré comme euclidien, car le modèle euclidien conceptuel est isotrope alors que l'espace perceptif ne l'est pas. Il en va de même pour l'espace sonore, ainsi que pour les intuitions spatiales qui accompagnent le rêve, les rapports d'idées, les couleurs... Cléro (2000) estime d’ailleurs que l'espace n'est pas un cadre vide (kantien) dont on disposerait a priori. Au contraire pour lui chaque perception engendre, hic et nunc, son propre espace. Ceci est certainement exact, mais n'empêche pas que nous disposions par ailleurs d'autres espaces, conceptuels et vides ceux-là, parmi lesquels nous pouvons choisir librement pour construire une image scientifique : dans ces cas il ne s'agit plus de perception mais d'intellection.
Fig. 4 : Les divers espaces mathématiques sont isotropes ; les deux plus utilisés sont cerclés. Schéma extrait de Atlas des Mathématiques, Fritz Reinhard et Heinrich Soeder, La Pochothèque, Livre de Poche, 1997.
Techniquement, les plus utilisés parmi ces espaces sont, outre le familier diagramme cartésien orthogonal, le semi-logarithmique, le bi-logarithmique, le triangulaire, le gaussien, le log-gaussien, le Rosin-Rammler, le Frosch und Vogel, etc. Ils sont souvent proposés dans le commerce sous la forme de papiers gradués.
3. Le point expérimental
- Note de bas de page 2 :
-
Cette analyse concerne les images construites par points ou séries de points, et ne s’applique pas, par exemple, à une photographie d’organe, de plante, ou de corps céleste. Ces dernières sont des images-sources.
- Note de bas de page 3 :
-
Par exemple la température et la pression d’un gaz dans une chaudière, ou la vitesse et la position d’un projectile sur sa trajectoire.
Ensuite il faut introduire et préciser la notion de point expérimental, qui constitue le matériau de base de tout le travail d'élaboration2. Le point expérimental est un ensemble de nombres représentant chacun la valeur numérique d'une variable différente, mais correspondant tous à une entité déterminée ou à un même processus3. Ces points sont disposés par nous dans un espace de travail, qui n'a rien à voir avec l'espace physique du monde naturel dont ils sont extraits, et dont on a parlé plus haut.
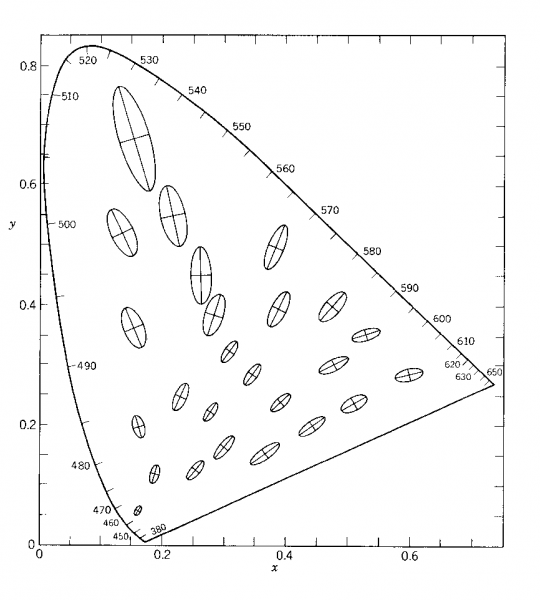
En théorie il s'agit bien de points (une grandeur physique ne peut avoir plusieurs valeurs à la fois), mais en pratique nous ne pouvons jamais déterminer leur emplacement exact. Ce que nous mesurons peut bien être représenté par un point dans un espace, mais le point réel ne coïncide pas nécessairement avec lui. Tout au plus peut-on calculer, autour de notre point hypothétique, une zone dans laquelle le point réel a des chances de se trouver. Il y a à cela deux raisons. La première est instrumentale et tient à la précision de nos appareils de mesure et de nos méthodes d'analyse. Il est possible d'évaluer cette erreur de mesure, que les progrès des appareils font sans cesse diminuer, mais il est évidemment impossible de l'annuler. La seconde tient aux facteurs du milieu, nombreux et non identifiés, qui n'ont donc pu être contrôlés. Ils ont pu varier à notre insu et exercer une influence perturbatrice. Dans une représentation à 2D, reprenant deux variables sur lesquelles nous faisons une erreur différente, les points deviennent des ellipses, appelées ellipses de dispersion, dont la taille reflète la probabilité estimée de la présence du point en leur sein (fig.5).
Si d'autre part on travaille à l'échelle subatomique, une autre limitation apparaît : le processus de mesure altère le processus mesuré d’une façon qui cesse d’être négligeable. Il s'agit d'une limite physique infranchissable, exprimée numériquement dans la célèbre relation d'incertitude d'Heisenberg. A cette échelle, un corpuscule ne peut plus être décrit que comme un nuage de probabilité, ce qui a entraîné une crise du concept de réalité. L’interaction sujet/objet commence donc déjà bien en amont de la perception.
Soit à présent un espace de travail dans lequel nous avons réuni plusieurs points expérimentaux ayant trait à la même entité ou au même processus. On admet que de tels groupes de points expérimentaux peuvent valablement être considérés globalement : ce ne sont pas des semis de points indépendants mais ils forment des ensembles dont il est possible de déterminer la structure. En d'autres termes ils possèdent une identité collective, garantie par leur identité de provenance.
Fig. 5 : Les ellipses de MacAdam. Pouvoir de discrimination des couleurs (à luminance égale) selon deux dimensions : saturation et teinte
4. L'inférence statistique, le hasard et les modèles
Au centre du travail d'élaboration, on trouve invariablement deux procédures : l’analyse statistique et l’inférence logique. C'est le grand statisticien Sir Ronald Fisher qui en 1935 a établi solidement cette thèse. Il s'agissait en fait d'axiomatiser et de formaliser les manipulations à appliquer aux données brutes pour en extraire une information significative. On pourrait même préférer dire que l'information ne préexiste pas dans les données : elle ne prend ce nom, cette forme et cette fonction que dans l'acte même du traitement, voire déjà lors de la collecte. D'autre part, il ne s'agit que d'une face du processus cognitif, car l'élaboration de modèles interprétatifs fait appel à des facultés mentales encore différentes, et sur lesquelles on sait peu de choses.
Mais revenons à Fisher et à sa méthodologie. Elle présuppose que l'on souscrive à quelques axiomes qui sont, n'hésitons pas à le souligner, de l'ordre du credo, de l'acte de foi :
- Note de bas de page 4 :
-
"Inductive inference is the only process... by which new knowledge comes into the world."
-
le monde continuera comme par le passé ;
-
il est licite de remonter des effets aux causes ;
-
bâtir une hypothèse générale à partir d'une observation particulière (inférence inductive) ne procure aucune certitude, mais c'est le seul processus par lequel un savoir nouveau peut être acquis4.
On notera que par ce dernier point Fisher annonce les thèses de Karl Popper, et décrit un mécanisme semblable à celui que Peirce appelait abduction. Quant aux deux premiers points, ils impliquent une adhésion totale au déterminisme. La thèse de Fisher revient à affirmer que la position d'un point expérimental dans un espace est entièrement déterminée par des facteurs qu'on ne pourra certes jamais repérer tous, mais néanmoins réels.
Soit donc un ensemble de points expérimentaux que nous disposons dans un espace choisi : ils forment ce qu'on a coutume d'appeler « un nuage ». Cependant, la forme de cet ensemble de points dans notre espace de travail ne correspond pas à une forme semblable dans le monde réel. Il a seulement une forme (espérée) au sens mathématique. Nous procédons ainsi à une spatialisation de cette forme, et plus précisément à sa visualisation. La première hypothèse est de supposer que ce nuage possède une identité collective et qu'une loi en unit les points. Cette loi est conçue dans la sphère mentale et formulée par une équation mathématique. En tant qu'équation, elle est un pur être mathématique abstrait, qui n'a nul besoin d'une matérialisation physique. Certains mathématiciens d'ailleurs, dont Bourbaki, sont hostiles aux représentations graphiques d'équations, qu'ils estiment trompeuses et étrangères à la nature même des êtres mathématiques. Néanmoins dans notre cas, la représentation graphique est universellement adoptée, et portée sur le même espace que le nuage de points. C'est donc sous le régime visuel que s'opèrent la rencontre et la confrontation du réel avec le mental.
L'équation choisie est supposée exprimer la loi qui unit les points : elle en constitue le modèle. Sous sa forme générale la plus complète, elle comporte :
-
une variable dépendante : y
-
des variables indépendantes identifiées : x1, x2, ... .xn,
-
des paramètres : p1, p2, …pr,
-
un terme aléatoire : ε
soit : y = f(x1, x2, …xi … xn, p1, p2, … pj …pr ) + ε
- Note de bas de page 5 :
-
Le célèbre rasoir d’Ockham ou principe de parcimonie conseille de ne pas faire intervenir plus de facteurs que nécessaire, il n’implique nullement que le monde est simple (cf. Hoffman, 1997). Ne pas s’y conformer mène à surparamétriser.
- Note de bas de page 6 :
-
… quoi qu’en pense Norbert Wiener (1962 : 10) qui le considère « comme une partie de la trame et de la nature de la Nature. »
Théoriquement, si on pouvait identifier toutes les variables xi et connaître la valeur exacte de tous les paramètres pj, ε serait = 0 et il n’y aurait pas d’ellipse de dispersion. De façon générale, plus n est grand, plus ε est petit. Si ε est élevé par rapport à f(x, p) il peut en venir à noyer l’information utile. En théorie du signal, on mesure cet effet par le rapport signal/bruit. La signification du terme ε vaut d'être discutée. Si un point expérimental occupe une position déterminée dans l'espace de représentation choisi, ce n'est pas par hasard, c'est par l'effet conjoint de m facteurs. Parmi ces m facteurs5, la loi supposée (hypothétique) en a explicité n < m, et les écarts entre valeurs calculées et valeurs observées sont le fait des facteurs non identifiés. On les traite globalement à l'aide du concept de hasard. Ils sont supposés résulter de causes multiples, indépendantes et relativement mineures. Cela ne signifie donc pas qu'elles n'existent pas, mais seulement qu'on les ignore. L’idée répandue selon laquelle elles ont tendance à se compenser est naïve et mythique. Le hasard n'est pas une sorte de force de la nature6, un principe autonome et fatal, c'est le nom que nous donnons à l'ignorance des causes. Le terme ε, qui en regroupe les effets, doit être considéré comme un résidu d'intelligibilité.
- Note de bas de page 7 :
-
Cela consiste à vérifier que ε ne manifeste aucune corrélation avec un facteur connu et mesurable.
Tout bon chercheur sait qu'il a intérêt à analyser la structure de l'erreur7 : cela lui permet souvent de repérer une variable jusque-là négligée et par là de réduire encore ε.
5. Le transit par le visuel et ses conséquences sémiotiques
- Note de bas de page 8 :
-
Cette observation met à mal la prétention du linguistique à l’emporter par son pouvoir sur tout autre système, supposé réductible à lui. Barthes, qui n’en doutait aucunement, avait pris cette certitude chez Hjelmslev (1968 :138) : « en pratique, une langue est une sémiotique dans laquelle toutes les autres sémiotiques peuvent être traduites, aussi bien toutes les autres langues que toutes les structures sémiotiques concevables. »
Dans la pratique scientifique humaine usuelle, on constate que la plupart des informations transitent par le canal visuel, quelle que soit leur nature dans le monde naturel, et nonobstant le fait que la connaissance ultime, au niveau neuronal, est parfaitement amodale8. Donc le terminus de la démarche cognitive n'est pas une image, l'image n'est qu'un état intermédiaire. Le visuel est, chez l'homme, le canal le plus développé, tant en capacité (107 bits/sec, soit sept fois plus que le canal auditif) qu'en modalités perceptives (sensibilité, acuité, couleur, mouvement, formes...). Le chien, qui perçoit 1000 fois mieux les odeurs que nous mais voit beaucoup moins bien, doit catégoriser son univers différemment. De même les insectes, dont les antennes perçoivent et discriminent les substances volatiles à l'échelle de la molécule... Plus généralement, on ne peut accepter l’idée que nos modalités sensorielles, ensemble, épuisent tous les modes de manifestation du réel. Il suffit de penser à ce que serait notre science si nous avions dû la construire uniquement à partir de l’ouïe…
Le travail d'élaboration constitutif de l'image scientifique s'effectue donc sur des symboles. Bien des auteurs se sont émerveillés de la fécondité de cette méthode consistant à raisonner et à faire des opérations sur des signes (parmi les chimistes : Joachim Schummer, 1996 et Ursula Klein, 2001). Schummer propose pour ce travail l'expression « interprétation analogique », qui repose sur l'hypothèse d'une correspondance univoque entre le référent et son signe. A une transformation graphique (donc symbolique) du signe d'une molécule correspondrait potentiellement une transformation équivalente de cette molécule. Bien entendu à condition d'observer certaines règles d'interprétation, donc aussi de transformation.
Il n'y a sans doute pas lieu de s'extasier à cet égard sur le code de la chimie car bien d'autres systèmes jouissent de propriétés semblables : le plan d’architecte, la partition musicale... Ce qu'il faut au contraire expliciter, c'est le statut sémiotique de tous ces concepts :
- Note de bas de page 9 :
-
ou mixtes, si on suit C. Allamel-Raffin (2006), mais la nuance entre ces deux termes doit être creusée…
- Note de bas de page 10 :
-
La longue évolution au cours de laquelle cette optimisation s’est construite est décrite, pour la chimie, dans Edeline, 2010.
(a) Le transit par le visuel offre des avantages substantiels (Edeline, 2007 ; Klinkenberg, 2009). Il y est possible de recourir à la fois, dans le même énoncé, à des codes digitaux (lettres, mots, symboles spéciaux...) et à des codes analogiques bénéficiant de la bidimensionnalité des supports pour présenter richement les relations entre entités, dans un espace continu et débarrassé de ce quadrillage en colonnes et rangées qui alourdit tellement la présentation en tableau de chiffres. C'est pourquoi sans aucun doute ces systèmes, sans exception, sont tous hybrides9. L'aspect digital des symboles est économique en espace : les symboles Mg ou ♪ représentent des entités complexes dont la description précise exigerait beaucoup de place. Cette possibilité offerte par l’usage des symboles a été appelée compactification (Alunni, 2004) et n’est en somme qu’une des versions du processus de regroupement de l’information (Groupe µ, en préparation). L'aspect analogique par contre excelle à noter les relations, du fait de la transposition homéomorphique existant entre le designatum et son signe. Je préfère cette formulation en langage topologique à l’habituel recours au concept d'iconisme (à moins d'étendre considérablement l'acception de ce terme ! v.(b) ci-après). Schummer estime que s'il est possible de réaliser des « opérations dans le monde des signes » c'est parce que « le signe est modifiable ». Cette affirmation est inexacte car seule la partie iconique du code est modifiable : Mg et ♪ restent inaltérables. L'évolution a mené tous ces codes à un équilibre parfaitement optimal entre leurs composantes analogique et digitale10.
- Note de bas de page 11 :
-
Formulation latine suggérée par J.-M. Klinkenberg, communication personnelle.
(b) La grande caractéristique des codes est la règle du renvoi entre le signe et la chose signifiée, règle qu'on formule souvent par aliquid stat pro aliquo. Cette formulation ne fait malheureusement que « mapper » un ensemble sur un autre, de façon statique, c.à.d. sans tenir compte des relations que peuvent présenter entre eux les éléments de l'ensemble de départ. L'insuffisance de cette description a été bien aperçue dans le domaine linguistique, où la théorie du mot-étiquette a été abandonnée. Greimas est sans doute celui qui a le mieux démontré l'existence simultanée, dans une même unité lexicale, de sèmes nucléaires et de sèmes contextuels ou classèmes. Il y a donc lieu d'introduire une seconde règle, pour le renvoi des relations : aliquorum relatio stat pro aliquorum relatione11. Dans le cas d'un codage visuel non digital (en particulier : non linguistique) cette règle prend tout naturellement la forme d'un iconisme. Chaque règle de transformation engendre un type particulier d'iconisme (Edeline, 2009).
- Note de bas de page 12 :
-
La coïncidence n’est jamais parfaite mais nous poursuivons les efforts de mise en correspondance jusqu’à parvenir à une proposition acceptable, assortie de réserves probabilistes.
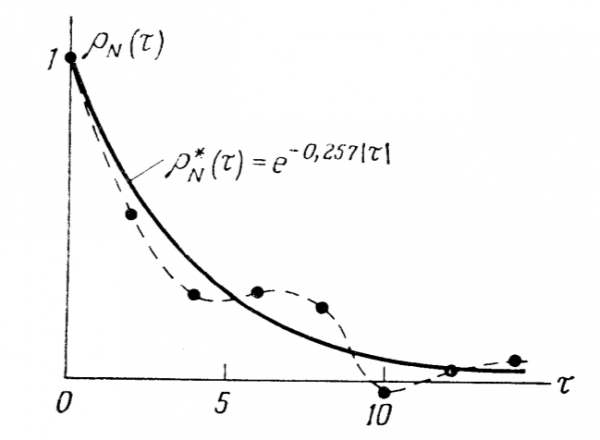
(c) Dans sa discussion des avantages des diagrammes en mathématiques et en physique, Saint-Ours (2004 :36) estime qu’ils rendent sensible ce qu’une équation ne fait que suggérer. Il reste cependant à expliquer pourquoi le sensible, malgré sa fausseté inhérente, serait plus probant que l’abstrait. Le fait est cependant étayé par de nombreuses déclarations de savants, telles que « Presque toute ma réflexion mathématique se fait visuellement et en termes de concepts non verbaux (R. Penrose, 1989). » Il est possible d’avancer l’explication suivante à la puissance probatoire du visuel par rapport à la formulation abstraite. Dans l’élaboration de l’image scientifique, le terme est considéré comme atteint lorsque deux formes coïncident12 (fig. 6 ) : on dit qu’il
Fig. 6 : La courbe en trait plein est « ajustée » aux 8 points expérimentaux, son équation (son modèle) est une exponentielle décroissante de paramètre 0,257. Il aurait été possible de trouver une courbe passant exactement par les 8 points, mais elle aurait comporté 8 paramètres au lieu d’un seul.
y a ajustement.. L’une de ces formes est celle que prennent les points expérimentaux dans l’espace de travail, l’autre est celle du tracé qui visualise un modèle mathématique abstrait dans ce même espace. Ce qui joue à ce moment est une application du principe d’identité. La forme « appartient » à l’objet (Edeline, 2007). Deux formes « raisonnablement » identiques concernent donc un objet unique, d’où nous acceptons que le modèle mathématique non seulement représente valablement l’objet ou le processus naturel, mais en quelque sorte fait partie de lui.
(d) Enfin, dernière importante remarque, le travail sur les signes, constitutif de l'image scientifique, fonctionne aussi bien dans le sens anasémiotique que catasémiotique. Dans la première fonction il aide à dégager la structure d'un modèle possible : c’est un outil de cognition. Dans l'autre il permet des « expériences de pensée », qui à leur tour suggèrent des expériences réelles à entreprendre.
6. L'ontologie réaliste
Le dernier point épistémologique à examiner est la question de savoir si ce que nous appelons l'information préexiste dans le réel - auquel cas nous ne faisons que la « découvrir » - ou si au contraire elle est intégralement issue du cerveau connaissant - et dans ce cas nous l'« imposons » au réel. Des traités entiers, pour ou contre une ontologie réaliste, ont été rédigés, aussi ne puis-je que traiter cursivement ce problème.
L'exigence méthodologique de Cléro (2000), qui consiste à refuser de se donner aucun concept ou aucune catégorie qui ne soit construite, permet d'éliminer beaucoup d'a prioris de type kantien, qui sont autant de dogmes. Le concept d'espace en est un bel exemple : pour Cléro, l'espace ne préexiste pas à la perception des objets, mais est construit en même temps que leur perception. L'idéal serait d'appliquer strictement et intégralement cette méthode pour tout le travail de la pensée, mais le peut-on ?
- Note de bas de page 13 :
-
C’est à nouveau Cléro (2003 :13) qui nous fournira la synthèse la plus claire de la position kantienne : « un concept n’a de valeur que s’il est un traitement de l’expérience (…) il n’est pas question de préconiser un fonctionnement vide du concept. Il n’a de sens qu’en se saisissant du donné (…) »
Lors de l'élaboration des données empiriques brutes dans l'image scientifique, on a vu qu'un important travail symbolique est réalisé, dans le but d'essayer de mettre en correspondance des schèmes mentaux avec les données expérimentales examinées13. Le schème tel que le concevait Kant, et reconnu par lui comme « mystère insondable », ne remplit pas l'exigence. Les schèmes d'action selon Piaget semblent mieux y répondre car ils consistent en simples aptitudes à manipuler les objets tout en les regardant, les écoutant, les soupesant, et mémorisant l'ensemble de ces perceptions. Le problème n'est cependant que déplacé, car il reste à expliquer d'où proviennent ces aptitudes. Sont-elles innées ou acquises, et alors comment ? Or l'école de Piaget, tout en se montrant réservée, voire hostile, quant à l'existence de structures innées, ne se prononce pas sur la capacité du cerveau à forger et/ou à héberger de façon durable des structures qui sont si efficaces pour assurer notre prise sur les choses. Elle ne se prononce pas vraiment non plus sur cette efficacité : est-elle posée seulement comme possible et susceptible d'être améliorée par le jeu des accommodations, ou au contraire est-elle, par hypothèse ou par principe, envisagée comme totale et parfaite ?
Piaget raisonne en fait comme si ces structures d'ensemble étaient comme déposées d'avance dans les potentialités du cerveau, mais devaient être réajustées sur le donné sensoriel par ce qu'il appelle des accommodations. On se trouve donc, une fois encore, en face d'un a priori, inné. On peut cependant se faire une idée plus précise de la nature de cet a priori en examinant attentivement le texte (Piaget, [1956], 1970 : 85-88) : tout repose sur des compositions d'actions, permettant des « généralisations constructives ». Cette aptitude, dont il faut bien accepter qu'elle soit innée, est donc la faculté de mise en rapport.
D'autres auteurs, dans d'autres contextes (p. ex. l'ethnographie chez Claude Calame, 1983), ont eux aussi débouché sur la constatation de l'existence, universelle semble-t-il, d'une telle faculté. Est-il impossible de la naturaliser à son tour ? Pour y parvenir nous aurons à faire un détour par Derrida, ou plus précisément par l'analyse serrée que fait Christopher Norris de sa Mythologie blanche (2008).
Derrida conteste la position du linguiste Benveniste (poussée jusqu'à l'absurde chez Sapir & Whorf) selon laquelle les outils intellectuels dont nous disposons, i.e. les catégories que nous formons, découlent intégralement de la langue que nous parlons. Derrida relève qu'il s'agit d'une confusion, dans le chef de Benveniste, entre les catégories particulières et l'aptitude à former des catégories, qu'il appelle catégorialité. Cette dernière est la précondition pour opérer un jugement quel qu'il soit. La catégorialité étant la faculté de comparer des entités et de les rassembler selon des caractères déterminés, nous retrouvons bien là la faculté de mise en rapport requise par l'approche de Piaget.
Le dernier maillon de notre argumentation, dont l’illation aura été bien complexe et délicate à établir, consistera à réduire la catégorialité à la structure de la connaissance (visuelle) élémentaire, laquelle, rappelons-le (Edeline, 1991 ; Groupe µ, 1998) fournit simultanément des entités et des rapports entre ces entités, soit l'essence même de la catégorie, grâce au mécanisme permettant la détection des qualités TRANSlocales. En effet, qui dit translocal implique la comparaison de zones voisines, la certitude que le monde est un et qu'il peut exister des rapports entre zones voisines. Créer une catégorie, c’est à la fois grouper des éléments sur la base de caractères communs et entériner leur différence par rapport à tous les autres éléments, d’où la formule Qui unit divise. On retombe ainsi sur la détection des dipôles et la boucle se referme : ce mécanisme est inscrit dans la structure de nos organes sensoriels, il est inné, mais son maintien témoigne de sa valeur de survie, donc aussi de son adéquation au monde (autre formulation de la théorie de la résonance mentionnée par Chazal, 1997) tout en expliquant la surprenante efficacité des mathématiques à décrire le monde (efficacité que Wigner, 1960, dans un texte célèbre, trouvait « exagérée »). Notre aptitude à former des catégories répond ainsi au fait que le monde est catégorisable.
En fin de compte, et contrairement aux affirmations de Piaget, l'origine sensorielle, non seulement des connaissances mais des mécanismes de la pensée, se trouve démontrée.
7. L'anti-réalisme textualiste
II règne actuellement un assez puissant courant philosophique anti-réaliste, forme extrême prise par l'empirisme anglo-saxon. Cette thèse est défendue notamment par Rorty, Putnam et d'autres (pour une étude détaillée de cette tendance, v. Norris, 2008). La question peut se reformuler ainsi : les lois du monde sont-elles commensurables à notre esprit ? Ou encore : la science peut-elle tenir un discours adéquat au réel ? Si ce n'était pas le cas, tout le travail dont il a été question plus haut serait vain. Estimer qu'un modèle rationnel du monde est possible, ou au contraire à jamais irréalisable, est une option métaphysique. Pour le progrès de la science, il suffit d'admettre la thèse popperienne selon laquelle les modèles sont perfectibles.
Dans ce contexte, il n'est pas possible d'éviter de prendre position quant à la sociologie de la connaissance dans sa variante constructiviste. Celle-ci a pour avocat le plus véhément, en terre francophone, Bruno Latour. Sa position vis-à-vis des modèles est des plus radicales : « Toute préférence pour un type déterminé d'interprétation n'est basée ni sur sa valeur cognitive, ni sur des caractères pragmatiques issus du système représenté, mais résulte de la compétition sociale entre groupes de scientifiques tâchant d'imposer aux autres leur mode d'interprétation. » (Latour et Woolgar, 1986)
On ne niera pas, bien entendu, l'existence de facteurs affectifs et sociaux, motivations qui lancent le chercheur scientifique dans un travail obstiné de collecte de données expérimentales, puis d’élaboration de celles-ci. Le chercheur en fait relève un défi, celui de réduire le déficit d’intelligibilité, écart moteur de l’entreprise, face à des données qui résistent à l’interprétation. Un univers incompréhensible est angoissant, et le travail scientifique n’est pas autre chose qu’une tentative pour dissoudre cette angoisse. Mais il est clair que les facteurs psychologiques en viennent toujours, tôt ou tard, à céder devant l'afflux des données, ou mieux sous ce qu’Einstein appelait « la pression irrésistible des faits ».
Or, pour les anti-réalistes, toute représentation est une « horreur méthodologique » (Zeidler, 2000). Latour précise même que notre maîtrise épistémique du monde se limite à celle de l'espace graphématique bidimensionnel des inscriptions : la feuille de papier ou le tableau noir sur lequel nous gribouillons un schéma ou une formule. Quant aux conventions pour noter la tridimensionnalité, elles sont explicitement associées à une « anomie perceptuelle et épistémique » (Francoeur, 2000).
Je suis évidemment en total désaccord avec ces idées, et partage le point de vue de Christopher Norris, qui n'hésite pas à parler à ce sujet d'une « mystification textualiste » (Norris, 2008) dont le point d'aboutissement est cette formule qui se veut définitive : « II n'y a que des textes ! », en déniant à ceux-ci tout rapport pertinent avec le monde naturel.