Le diagramme entre perception visuelle et mathématique

0. Introduction

La question de la définition de l’image scientifique par rapport à d’autres outils de représentation et d’expérimentation et d’autres statuts de l’image – tel que le statut artistique ‑ est évidemment très délicate. On voudrait essayer de proposer quelques éléments de réflexion à partir de trois questions principales :

1. Est-ce qu’on peut chercher à élaborer une définition de l’image scientifique qui soit commune à toutes les disciplines scientifiques ou, le cas échéant, susceptible d’être partagée par les disciplines qui se donnent pour finalité d’étudier ce type de production (entre autres, épistémologie, philosophie des sciences, histoire des sciences, sémiotique) ?

2. Quels types de rapport s’établissent entre les images scientifiques et les images artistiques ? S’agit-il d’une différence ontologique ou bien pragmatique, voire dépendante des usages et des types d’implémentation publique ? On essaiera d’esquisser une réponse à travers certains exemples d’images artistiques insérés dans les ouvrages de vulgarisation scientifique. On essaiera aussi de distinguer les rôles des images artistiques des vues d’artiste qui peuplent la littérature scientifique, surtout en astrophysique.

3. Est-ce que le dispositif de l’image trouve son terme opposé dans le texte verbal, suivant l’ancienne distinction entre analogue et digital, entre densité figurative et écriture par éléments arbitraires et disjoints ? Est-ce que par contre l’image trouve son terme opposé dans le langage formel des mathématiques ?

1. Esquisses pour des définitions de l’image scientifique : à partir du diagramme

Il est évident que chaque discipline scientifique, et peut-être chaque équipe et chaque laboratoire, peut-être même chaque scientifique, peut ambitionner d’avoir sa propre définition d’image scientifique et d’y faire rentrer des schémas ou bien d’autres types de visualisations verbo-visuelles. Comment faire donc pour se rapprocher d’une définition partageable commune et qui puisse identifier non seulement ce qu’est une image, mais ce qui vaut comme une image, comme par exemple un tableau de chiffres qui donne tous les paramètres nécessaires pour composer une visualisation en astrophysique ? De quoi la distinguer ? Quelles manifestations langagières lui opposer ?

Si trouver une définition de l’image scientifique commune à toutes les disciplines scientifiques plus ou moins dures est une ambition trop grande et peut-être trompeuse, il serait plus raisonnable à cette occasion d’enquêter sur les raisons des images et sur leur opérativité dans le cadre d’une discipline telle que l’astrophysique par exemple.

Je précise déjà que nous établirons une distinction entre des dispositifs qui visent la stabilisation visuelle des résultats de recherche (outils de représentation) – qui intéressent surtout la vulgarisation scientifique et sur lesquels on reviendra à propos des relations entre art et vulgarisation ‑ des dispositifs qui, en revanche, « aident » la réflexion et le travail en cours, voire qui les supportent et les construisent (outils d’expérimentation). On peut déjà affirmer que ces deux types de dispositifs ne se distinguent pas ontologiquement mais de manière pragmatique, à savoir qu’une image ou un graphique ou un schéma peuvent facilement être utilisés à la fois comme des outils de représentation et comme des outils d’expérimentation. D’ailleurs, certaines images considérées comme des représentations utiles pour la vulgarisation des savoirs ‑ à savoir des images stabilisant l’iconographie d’un objet accepté sans controverses ‑ peuvent ensuite redevenir opératives, à savoir être remises en jeu comme des images qui donnent des indications sur leurs paramètres de fabrication, sur les paramètres pertinents pour une recherche ultérieure et être ainsi utilisées comme un nouveau point de départ de l’expérimentation. Non seulement nous ne pourrons pas hypostasier chaque type de forme visuelle en un seul et unique fonctionnement, mais souvent ce seront des images en série ou des chaînes de dispositifs qui nous permettront d’identifier un fonctionnement. Dans ces séries et enchaînements, les mêmes dispositifs visuels peuvent assumer d’une fois à l’autre des rôles différents : comme on l’a déjà dit, ils peuvent stabiliser une iconographie ou bien redevenir opératifs et manipulables en vue de nouvelles recherches.

Peirce rejette du même mouvement le critère de la « ressemblance sensible » et celui du degré de conventionalité pour définir l’icône ; celle-ci est plutôt caractérisée en termes logiques, par sa « capacité à révéler une vérité inattendue » concernant son objet. L’exemple des deux photographies servant à tracer une carte renvoie à la méthode photogrammetrique certainement familière à Peirce par le biais de la géodésie. Dans cette méthode, on peut construire une carte, sous certaines conditions techniques, à partir de deux ou plusieurs photographies d’un site donné prises de points de vue opposés, moyennant des opérations de réduction analogue à celles du levé direct. La photographie couplée a reçu beaucoup d’autres usages, notamment dans divers types d’analyse du changement. Comme dans le cas de l’enregistrement photographique des éclipses, ce qu’exploite la méthode n’est pas la ressemblance de chaque photographie à des objets particuliers, mais l’analogue idéal de la topographie que constitue la collation géométriquement déterminée des deux photographies (pp. 314-315).

Ce n’est donc pas une ressemblance sensible (sensous resemblance) mais bien une similitude idéale (likeness) qui est manifesté par le dispositif du diagramme qui doit nous guider dans notre enquête sur l’image scientifique et ses rapports avec d’autres outils de représentation et d’expérimentation. Pour pouvoir étudier les fonctionnements qui sont transversaux (la similitude idéale) par rapport aux apparences visuelles (ressemblance sensible), il faut partir non pas de l’analyse des instruments imageants eux-mêmes mais bien des problèmes d’une fois à l’autre différents à l’intérieur d’une recherche scientifique qui engage des images et des dispositifs verbo-visuels. Comme on l’a dit auparavant, il faut partir des raisons de la fabrication d’images (leur pourquoi) et non pas des images elles-mêmes. D’ailleurs le « pourquoi » des images engendre une réflexion sur les pratiques scientifiques et non seulement sur les textualités scientifiques – c’est pour cette raison qu’il est nécessaire d’aborder la définition d’image scientifique en la mettant en relation avec les pratiques artistiques, et plus précisément en étudiant comment les images provenant du domaine artistique peuvent fonctionner dans le domaine de la littérature scientifique. On verra tout cela de plus près dans le § 2.

1.1. L’exemple du diagramme et son opérativité

L’exemple du diagramme et de sa définition est très éloquent par rapport à notre problématique définitoire, le diagramme étant entendu souvent comme une visualisation schématique dans laquelle est inscrit un court texte verbal ou bien des symboles. Parcourir brièvement les définitions de diagramme pourrait nous aider à comprendre comment Peirce a pu généraliser le fonctionnement du diagramme mathématique en un dispositif nécessaire pour comprendre le déploiement de la pensée déductive, à savoir en un dispositif qui garde les traces de son fonctionnement en mathématique mais vaut pour décrire la conduite de tout raisonnement nécessaire. À travers cet exemple, on pourra se rapprocher de notre idée de départ : comprendre et expliquer les objectifs et les fonctionnements des images – qui peuvent éventuellement être partagés par d’autres formes visuelles normalement appelées schémas ou graphiques – sans partir forcément d’une identification et d’une classification a priori des formes visuelles elles-mêmes.

Dans le cadre d’une recherche sur le diagramme, il faut également distinguer une définition triviale fondée sur les apparences visuelles d’une définition visant à identifier un outil constitutif de la pensée.

Une définition triviale est la suivante, publiée sur Wikipedia :

Plutôt qu’identifier le diagramme avec une certaine forme visuelle, il faut revenir à la tradition de la pensée sémiotique peircienne sur la notion de diagramme qui recouvre des phénomènes apparemment très divers mais liés, comme on l’a dit toute à l’heure, par des fonctionnements apparentés. Pour ce faire il nous semble utile de revoir comment la notion de diagramme s’est constituée en retournant à ses sources.

En ce qui concerne la première polarité, Peirce affirme :

D’une certaine manière, le diagramme serait donc scindé en deux : un diagramme en tant que Token singulier, et un diagramme qui donne les règles de lecture pour comprendre ce Token comme un Type.

En ce qui concerne la deuxième polarité, comme l’affirme Chauviré, pour Peirce :

Je ne pourrai pas parcourir dans son entier ce processus qui porte de la notion de diagramme entendu comme représentation visuelle objectivée et isolable jusqu’à la notion portant sur une conduite de la pensée qui exploite le côté opérationnel de l’iconicité. Ce que je voudrais retenir est que la notion de diagrammaticité rend précisément compte de l’articulation entre la visualisation et la transformation des relations entre les parties qui composent un objet d’une part et les étapes d’un processus de la pensée visant à connaître mieux l’objet visé ‑ grâce à cette visualisation manipulable justement ‑ de l’autre.

La diagrammaticité est définissable enfin comme une manière de bénéficier des ressources cognitives de la plasticité spatiale, voire de la manipulabilité et de la déformabilité rationnelle des visualisations. Elle opère comme un « flat laboratory », comme le dirait Latour (2008), où la réalité, et la réalité mathématique notamment, peut être comprise et transformée.

1.2. Le diagramme et les formes iconiques

Comme on l’a déjà esquissé, le fonctionnement diagrammatique peut concerner des photographies, des formules algébriques, des diagrammes proprement géométriques.

En revenant à présent à l’origine mathématique du diagramme, l’expérimentation offerte par le diagramme est, selon Peirce, ce qui distingue la procédure déductive théorématique du raisonnement corollariel, ce dernier ne concernant que des inférences purement analytiques, donc appartenant à la logique et non pas à l’épistémique. Comme l’affirme Chauviré (2008) en délinéant la différence entre théorématique et corollariel :

[D]eux cas peuvent se présenter : soit la conclusion est directement lue dans le diagramme initial par simple inspection, c’est-à-dire que les relations qui rendent possibles la conclusion sont immédiatement perçues sans qu’on doive retoucher le diagramme [corollariel] ; soit il est nécessaire de le modifier par des constructions supplémentaires [théorématique] […]. L’adjonction de telles constructions est dépeinte comme une expérimentation effectuée sur le diagramme, analogue à celle pratiquée en physique et en chimique sur un échantillon (p. 36, nous soulignons).

L’expérimentation en mathématique passe par la spatialisation des grandeurs spatiales et non spatiales (relations logiques, etc.) et par l’introduction de « lignes subsidiaires » aux lignes du dessin qui suivent fidèlement les prémisses. Ces lignes subsidiaires permettront d’introduire des idées nouvelles car elles rendent saisissables des nouvelles formes qui n’étaient que latentes. Cette adjonction est faite par des règles et permet de voir des formes ressortir de la constitution d’une totalité :

…Le Grundsatz de la Rhétorique formelle est qu’une idée doit se présenter sous une forme unitaire, totalisante et systématique. C’est pourquoi maints diagrammes qu’une multitude de lignes rend compliqués et inintelligibles deviennent instantanément clairs et simples si on leur ajoute des lignes ; ces lignes supplémentaires étant de nature à montrer que les premières qui étaient présentes n’étaient que les parties d’un système unitaire (Peirce, 1931-35, 2.55, nous soulignons).

Ce sont ces formes qui nous rendent perceptivement évidentes la nécessité des conclusions, et c’est pour cela que Peirce a toujours rapproché la contrainte exercée sur nous par une perception ordinaire et les conclusions mathématiques qui s’imposent à nous comme nécessaires : elles sont toutes les deux caractérisées par l’émergence de configurations qui ne peuvent qu’être comme elles sont. Pour Peirce, en fait, la vérité perceptive est aussi irrésistible que la vérité mathématique :

Cette contrainte irrésistible du jugement de perception est précisément ce qui constitue la force contraignante de la démonstration mathématique. On peut s’étonner que je range la démonstration mathématique parmi les choses qui relèvent d’une contrainte non rationnelle. Mais la vérité est que le nœud de toute preuve mathématique consiste précisément dans un jugement à tout égard semblable au jugement de perception, à ceci près qu’au lieu de se référer au percept que nous impose la perception, il se réfère à une création de notre imagination (Peirce, 1931-35, 7.659).

Ce que nous voulons suggérer par cet excursus dans la théorie du diagramme est que tout support, dans notre cas visuel, qui devient un lieu de travail et d’expérimentation de ce type devrait pouvoir être interprété comme un dispositif qui fonctionne diagrammatiquement. Mais nous verrons cela toute à l’heure, en passant à travers d’autres questions qui devraient également nous aider à délimiter les rôles de l’image en astrophysique dans la vulgarisation scientifique et dans les publications pour les spécialistes.

En procédant par une comparaison entre pratiques d’utilisation d’images en science et en art, nous essayerons de voir si nous pouvons distinguer dans l’image scientifique une forme de nécessité différente de celle qui prévaut pour l’image artistique…

2. La vue d’artiste et l’image artistique dans les publications scientifiques

La deuxième question qu’on s’est posée pour poursuivre notre réflexion concerne la spécificité de l’image scientifique par rapport à d’autres produits de l’activité humaine : la comparaison avec les règles internes au domaine de l’art, qui apparemment se place aux antipodes de la recherche scientifique, nous semble nécessaire.

Pour nous interroger sur cette question, nous allons faire référence à un ouvrage de vulgarisation scientifique de l’astrophysicien Jean-Pierre Luminet qui utilise des vues d’artistes et des images historiquement attestées comme artistiques dans la procédure d’exposition scientifique ; nous allons essayer de comprendre comment elles diffèrent des images contenues dans les articles de recherche.

Est-ce que cette vue d’artiste qui prend une image de l’artiste hollandais Escher pour modèle (Figure 1), publiée dans Le destin de l’Univers. Trous noirs et énergie sombre de 2006, ouvrage adressé à la communauté élargie des collègues astrophysiciens, peut être considérée, non pas comme nécessaire à la démonstration scientifique, mais du moins utile pour l’argumentation et éclairantes pour cerner le fonctionnement d’un phénomène difficile à saisir ?

Figure 1 : Jean-Pierre Luminet (d’après Escher), Le Trou noir, lithographie et dessin, 66 x 91cm, 1992.

À travers ce type de représentations visuelles, Luminet ne vise pas simplement à actorialiser les recherches sur l’attirance du vide d’un trou noir en mettant l’observateur face à la représentation analogisante d’une sensation sensori-motrice qui pourrait lui être causée par la chute à l’intérieur d’un trou noir ‑ l’image met en scène en fait le vertige de l’engloutissement d’un point de vue humanisé. Bien plus que cela, ce type d’image vise à justifier les fondements mêmes des recherches scientifiques. En fait, à travers ces images, Luminet montre comment les arts ont eu comme sujet d’enquête les trous noirs psychiques sous les formes les plus diverses ‑ la peur de l’abîme sans fond, la peur de la disparition dans le noir, etc. – et comment les topoï littéraires et artistiques ont influencé les chercheurs, en jouant un rôle majeur dans la créativité scientifique et notamment dans la conception des théories.

Si on regarde attentivement l’image construite par Luminet d’après Escher, elle met en scène un espace construit sur des incongruences topologiques effrayantes et sur des architectures illogiques et non praticables visant à montrer que le trou noir est un espace dévorant et duquel rien ne pourrait ressortir. D’ailleurs, Escher est l’artiste qui plus que tout autre a su décrire l’ouverture vers le vide, la montée qui se transforme en une chute aspirée ; en un mot, il est l’artiste du vertige, et du renversement des perspectives, ce qui exemplifie bien le fonctionnement supposé des trous noirs. Plus précisément, cette image représente un gouffre à l’intérieur duquel sont aspirés des dés. Les figures des dés mettent en scène la tentative scientifique de brider le hasard en le rapportant à des résultats contrôlables (les six faces du cube). Ils représentent des instruments du calcul de ce qui se passe et de ce qui n’est pas entièrement maîtrisable. Emportés par la force attractive du trou noir, les dés tombent dans une fissure tectonique et ils montrent ainsi le point-limite de la calculabilité scientifique : à l’intérieur de ce gouffre, il manquera un plan d’appui et ils ne pourront plus se stabiliser en une position qui manifeste un résultat. Ces dés sont donc une métonymie de tous les éléments prothétiques de l’être humain qui visent à brider l’indétermination. Le trou noir est au contraire un mouvement chaotique qui ne permet même pas une position d’observation statistique de ses turbulences. Aucune maîtrise de cet espace dévorant n’est possible : toute position des dés ou de l’observateur est provisoire, fuyante. Les faces des dés deviennent de plus en plus indiscernables, plus on descend dans le puits. Leur pluralisation met encore davantage en valeur leur fonctionnement en tant que dispositifs pour construire et édifier des architectures théoriques possibles : leur chute est la débâcle de toute tentative de contrôle.

Il nous semble qu’ici la vue d’artiste vise à exemplifier des conflits de forces et des tensions entre perte d’orientation et recherche de repères qui sont à l’origine de la conception scientifique des trous noirs. On s’aperçoit qu’à travers cette image, Luminet vise à construire une archéologie de l’être concevable même du trou noir ; toutes les références à la littérature et à l’histoire de la culture qu’il établit se justifient à travers cette nécessité de remonter à l’origine même de la référentialisation.

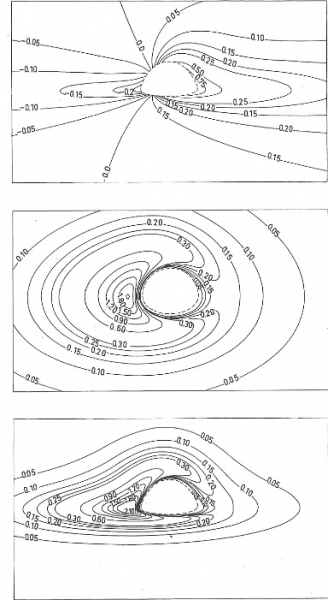
Tout se passe évidemment de manière très différente dans l’article de recherche, « Image of a Spherical Black Hole with Thin Accretion Disk » de 1979, publié sur la revue spécialisée Astronomy and Astrophysics, qui cherche non pas à imager, mais à calculer l’iconographie des trous noirs. La spatialisation des équations mathématiques en une série de visualisations (Figure 2) montre le travail de recherche des liens et des justifications mathématiques entre les nombreuses étapes du processus de visualisation d’un objet qui n’est que théorique, tels les trous noirs. Ici, la référence en question est donnée par la théorie de la relativité générale, et le public visé est la communauté restreinte des collègues spécialisés dans la topologie cosmologique.

Figure 2 : Jean-Pierre Luminet Courbes du disque d’accrétion selon différents points d’observation (Luminet, 1979, p. 234)

On s’aperçoit que la différence entre les deux genres discursifs de la littérature scientifique est déterminante dans le choix des images à montrer au public : dans l’article de recherche, il s’agit de rendre explicites toutes les étapes de la construction théorique et mathématique de l’objet de recherche ; dans l’ouvrage de vulgarisation, en revanche, il ne s’agit plus de rendre explicites les connexions et les liens entre étapes du parcours de référentialisation théorique, mais bien au contraire de justifier en amont l’origine culturelle de cette référentialisation.

La chose bizarre qui résulte de cette comparaison me semble être que c’est paradoxalement l’image artistique qui permet au lecteur de l’ouvrage scientifique de faire un pas en arrière sur les fondements de ces recherches : si dans l’article de recherche, les fondements de la référentialisation concernent la théorie de la relativité générale et les équations qui en découlent, dans l’ouvrage de vulgarisation, les fondements de la référentialisation concernent des configurations sémantiques fondées sur des formes de vie partagées par la culture occidentale. D’une certaine manière, la référentialisation pertinente dans le genre discursif de la vulgarisation ne vient pas après celle des articles de recherche, en guise de simplification, mais elle se pose aux sources de la réflexion scientifique sur la relativité générale et sur les modèles théoriques qui peuvent expliquer des phénomènes difficilement saisissables. Mais ce qui est encore plus intéressant est que l’image d’après Escher, positionnée à la base d’une recherche théorique tentative sur des objets qui sont en train d’être étudiés pour la première fois, veut signifier aussi que l’utilisation d’une image artistique montre le lieu où la démarche scientifique cherche à résoudre ses limites ou ses hésitations, bref lorsque la science accepte ses contradictions sur les fondements de ses recherches et les fait momentanément coexister. C’est le lieu où cette coexistence des contradictions peut devenir une source de réflexion. On pourrait arriver à dire que la vue d’artiste de Luminet exemplifie la difficulté qu’a la recherche scientifique à ne s’appuyer que sur elle-même et sur les règles propres au domaine scientifique.

On s’aperçoit finalement que la problématique de la définition de l’image scientifique engendre précisément la question des genres discursifs de la littérature scientifique : est-ce que les images telle la vue d’artiste d’après Escher contenue dans l’ouvrage de vulgarisation sont scientifiques ? Ou au contraire, seuls les articles de recherche sont-ils à prendre en compte pour comprendre quels sont les fonctionnements des images scientifiques ? Il est difficile d’exclure la vulgarisation car, si on entend par image une configuration qui identifie un objet, il n’y aurait alors presque pas d’images dans les papers de recherche qui sont adressés aux collègues de la même spécialité ; il n’y a souvent que des tableaux de chiffres présentant des séries de résultats de mesure… Les images construites à partir des chromatismes et des textures figées établissant une iconographie sont employées surtout dans les ouvrages de vulgarisation adressés à la communauté scientifique élargie. Peut-on choisir alors la vulgarisation pour la communauté scientifique élargie comme genre textuel de référence pour notre définition, même si souvent les images ici contenues n’affichent pas les paramètres de leur production et reproductibilité ? Autrement dit : même si elles nient la possibilité d’être entendues en tant que lieux d’expérimentation ?

D’ailleurs, il ne faut pas oublier qu’il peut arriver que les images de vulgarisation soient exactement les mêmes que celles publiées dans les articles destinés aux revues spécialisées. C’est seulement leur positionnement dans la chaîne rhétorique de l’argumentation qui change. C’est le cas de l’image suivante (Figure 3), qui est à la fois le résultat final de l’expérimentation qui résulte de la série de visualisations de calculs (Figure 2) dans l’article spécialisé et une des images de départ pour la construction des simulations d’un voyage à l’intérieur d’un trou noir dans l’ouvrage de vulgarisation.

Figure 3. Jean-Pierre Luminet, Apparence lointaine d’un trou noir sphérique entouré d’un disque d’accrétion. Photographie virtuelle d’un trou noir, calculée en 1978 sur ordinateur (reprise dans Luminet, 2006, p. 284)

Publiée pour la première fois en 1979 dans la dernière page de l’article, « Image of a Spherical Black Hole with Thin Accretion Disk » de 1979, comme résultat final d’une expérimentation diagrammatique, elle est retenue dans l’ouvrage de vulgarisation Le destin de l’Univers : est-ce que cette image, qu’on peut considérer comme l’image résultant d’un travail de calcul des valeurs mathématiques, a le même statut dans l’article de recherche que dans l’article de vulgarisation ?

Dans le cas de l’ouvrage de vulgarisation, sa genèse n’est pas justifiée à travers les multiples passages qui l’ont rendue fabricable, et qui sont visualisés dans la Figure 2. C’est cela qui fait la différence : dès que l’image scientifique est isolée, dès qu’elle est soustraite à la chaîne de transformation de données ‑ ou des valeurs mathématiques ‑ qui l’a produite, son statut bascule ; elle devient forcément une image non-démontable, voire non justifiable par ses paramètres de production. Elle devient une image non-manipulable et son statut bascule vers l’exemplaire unique, vers la non-reproductibilité, vers le statut artistique. Elle se transforme en une image unique et figée comme le sont nécessairement les images artistiques, qui sont des originaux sacralisés. Publiée dans un genre textuel différent de la littérature scientifique, cette image se transforme : de résultat d’une moyenne de valeurs mathématiques, donc d’image manipulable et par conséquent diagrammatique, elle devient une image identifiant un objet. C’est à travers cette stabilisation et ce processus d’arrêt de la manipulation qu’on présente au public un objet qui a parcouru son chemin d’un statut « d’objet de recherche » à un statut d’« objet scientifique ».

On peut donc conclure que, à l’intérieur de la littérature scientifique, les rôles de la même image dépendent aussi des genres discursifs de la publication dans lesquels elle est insérée et de sa position à l’intérieur de l’argumentation ; on a vu que dans l’article de recherche, elle est justifiée par les étapes de sa construction (de la théorie physique aux modèles mathématiques, des équations aux diagrammes) tandis que dans l’ouvrage de vulgarisation, elle se manifeste comme unique et isolée, non supportée par des justifications mathématiques e donc sans « filiation » possible.

2.1. Entre visualisations, image et calculs

En ce qui concerne le domaine de l’astrophysique plus généralement, on s’aperçoit qu’il y a au moins trois sortes de représentations visuelles dans les publications de cette discipline. Des deux premières, nous avons traitées ailleurs de manière plus approfondie (Dondero 2009b) et nous allons donc passer très brièvement sur elles :

1. Le premier type relève des visualisations de données : les mêmes données ‑ qui sont des visualisations de valeurs choisies à partir des tableaux de chiffres obtenues par des mesures ‑ sont visualisées à travers des échelles et des couleurs différentes visant à valoriser des différences de température, de composition chimique, de vitesse, etc. Les visualisations n’instituent pas l’identité de l’objet scientifique à un phénomène, elles n’offrent pas une iconographie stabilisée d’un objet : en revanche, elles rendent pertinents des regroupements des données qui puissent répondre à des questionnements d’une fois à l’autre différents. Chaque visualisation de données répond à une série de questions ; les visualisations peuvent être comprises comme des exécutions des relations entre données récoltées et paramétrages choisis. Les visualisations sont donc des exécutions d’instructions de codages de données et, par conséquent, elles sont reproductibles par n’importe quel scientifique qui dispose des mêmes données, de mêmes paramètres et du même outil de visualisation. Elles se présentent normalement sur un écran d’ordinateur en un rapport paradigmatique les unes avec les autres et elles sont très rarement enchainées comme développement l’une de l’autre : elles construisent une parataxe. D’une certaine manière, elles ne font qu’actualiser des organisations méréologiques de données qui restaient virtuelles dans le tableau de chiffres dont elles émanent. C’est pourquoi nous devons distinguer ces visualisations qui « arrangent » et filtrent des données de manière toujours différente selon le besoin de l’investigation, des images qui par contre identifient un objet et qui l’instituent en une unité où chaque partie a un lien figé avec toutes les autres et avec la totalité constituée. Si les visualisations ne sont que des variantes d’un environnement virtuel composé par des données à façonner selon des exigences diverses, l’image qui identifie un objet institue une nouvelle iconographie.

2. Le deuxième type de représentation visuelle concerne justement les images identifiant un objet qui, à la différence des visualisations, visent la fabrication d’iconographies stabilisées. Ces images qui construisent une iconographie stabilisée d’un objet – lequel devient « objet » précisément grâce à l’image ‑, tendent vers le régime caractérisant les images artistiques où chaque trait est figé à l’intérieur d’une totalité non décomposable. Mais, comme on vient de le dire, le statut d’image identifiant un objet dépend du genre discursif aussi, elle ne l’est pas dans l’absolu. C’est ce qu’on a décrit par rapport à l’image des trous noirs (Figure 3) : cette dernière fonctionne comme une image d’objet si on la considère comme isolée par rapport à la chaîne de transformation qui l’a rendue possible, et insérée dans une publication de vulgarisation, mais elle fonctionne en revanche comme une image-visualisation (des valeurs mathématiques) si on la considère comme résultante d’une chaîne justifiée de calculs dans l’article de recherche. Si le rôle de l’image dans l’article de recherche est de mettre en valeur l’instrument (ou dans notre cas, les valeurs mathématiques) qui l’a produite, dans la vulgarisation par contre, l’image ne montre plus la relation avec son acte de production : en perdant sa justification énonciative, elle se rapproche du rôle des images artistiques, qui ne sont pas censées révéler leurs techniques d’instanciation. Elle devient une image non-scientifique, car elle a figé quelque chose ne permettant plus des manipulations et donc avancées de l’investigation. On pourrait donc affirmer que l’image qui stabilise une iconographie et qui est publiée notamment dans les ouvrages de vulgarisation fonctionne à l’instar des images artistiques, qui sont non-manipulables.

3. Nous identifions un troisième type d’image avec les visualisations mixtes comme celles qu’on a vues dans la figure 2, et qui peuvent être comprises comme des étapes de l’expérimentation qui peuvent aboutir dans la fabrication de l’iconographie des trous noirs (Figure 3). Les représentations visuelles dans la figure 2 engendrent en leur sein un processus d’expérimentation et de manipulation via les multiples spatialisations des valeurs mathématiques. Nous les appelons visualisations mixtes parce qu’elles sont produites par une spatialisation des équations, à savoir par une tentative de donner consistance spatiale à des opérations portant sur une réalité mathématique abstraite. C’est toujours difficile de concevoir que les équations puissent arriver à « énoncer » des représentations visuelles étant donné que la propriété principale de toute image a toujours été d’être le résultat local et figé d’une énonciation technologique. L’image, à cause de son ancrage dans un espace particulier, a toujours été entendue comme quelque chose de localisant et localisé dont il faut s’éloigner si on veut procéder à la généralisation. Ici les choses sont différentes : ce sont les équations qui donnent un ancrage et un statut de nécessité à l’organisation spatiale. C’est l’équation qui densifie l’image, qui l’enracine en une organisation topologique nécessaire. C’est l’équation qui offre les multiples possibles ancrages que l’image d’un objet théorique ne peut pas produire toute seule, mais c’est l’image qui offre aux équations un espace opérable, voire un espace d’expérimentation. La visualisation offre la forme aux valeurs des équations, mais en offre une forme manipulable et déclinable au pluriel. D’une certaine manière on pourrait dire que l’équation détermine et localise la spatialisation en lui offrant les coordonnés de l’opérativité, mais l’image localise elle aussi la généralité de l’équation en lui offrant une spatialisation qui peut éventuellement devenir le lieu d’introduction des lignes auxiliaires ‑ dont parle Peirce ‑ qui peuvent engendrer des nouvelles manières de voir l’objet qui est en train de se constituer. Ces images mixtes montrent le développement d’une manipulation diagrammatique, c’est-à-dire une construction ni totalement singulière et locale, ni totalement générale et globale. Toute diagrammaticité en fait est liée à des propriétés locales de l’espace (position, dimension, orientation) ‑ la visualisation étant enracinée dans un support matériel observable et dans la perception ‑ mais en même temps elle ambitionne de valoir pour plusieurs objets, c’est-à-dire pour les trous noirs en général. Ces images construisent à notre avis un raisonnement diagrammatique parce qu’elles montrent l’opérativité du scientifique sur une topologie donnée et en même temps affichent les résultats des calculs dont l’instance énonciative n’identifie pas une syntaxe figurative localisante une énonciation, mais une généralité. Ce qui différencie ces images des visualisations de type 1, c’est le fait que chaque visualisation mixte construit en son sein plusieurs formes, elle les condense en devenant une synthèse des différentes manières de constituer des organisations différentes des données. Au contraire, chaque visualisation de type 1 ne condense rien, elle ne vaut que comme un élément paradigmatique dans une série d’images construisant une parataxe. De plus, ces dernières sont des visualisations de données, tandis que les visualisations mixtes sont des visualisations d’opérations.

2.2. L’art et les mathématiques dans la représentation de l’Univers

Après cette brève analyse des représentations des trois noirs, on pourrait se demander : est-ce que, alors, l’image artistique n’a rien à faire avec les mathématiques ? Sont-ce les mathématiques, appartenant exclusivement à la construction de l’image scientifique, qui la distinguent de l’image artistique ? Nous allons envisager quelques exemples qui pourraient nous donner quelques ébauches de réponse négative à cette question. Nous essaierons de comprendre comment la topologie de l’image scientifique fonctionne par rapport à d’autres topologies dont le statut n’est pas scientifique, mais artistique : ces exemples rendent difficile une distinction nette entre les types d’espace spécifiques aux statuts artistique et scientifique des images.

Comme plusieurs chercheurs l’ont remarqué, il est plus fréquent qu’une image scientifique soit assumée comme œuvre artistique que vice-versa, mais il faut nuancer cette évidence. Précisément en se demandant : est-ce que la signification de l’organisation topologique de l’image dépend de cette question statutaire, une même organisation de l’espace pouvant être assumée par n’importe quel statut ? Est-ce que, vice-versa, le statut dépend de l’organisation spatiale de l’image ?

Dans le cas de l’image scientifique cette organisation en principe devrait être :

1. informative ‑ à savoir une organisation à partir de laquelle on peut obtenir des réponses par rapport à une question ou à un problème donné ;

2. digitalisable – à savoir constituée par des éléments disjoints ;

3. modulable ;

4. sa genèse est censée être reproductible par une communauté de chercheurs.

Toutes ces caractéristiques en principe ne devraient pas être partagées par l’image artistique.

Nous précisons que nous entendons par espace modulable un espace qui peut donner existence à des modules qu’on peut imaginer comme des sous-organisations et de regroupements divers et concurrentiels de données. Il est donc différent de digitalisable, car la propriété d’être digitalisable n’est qu’une qualité nécessaire de la propriété d’être modulable, à savoir ré-organisable à travers plusieurs ordres et faisceaux de critères.

Comme nous l’avons déjà affirmé auparavant, la littérature scientifique accueille en son sein des images qui ne sont pas proprement scientifiques si par image scientifique, on entend qu’elle est caractérisée par les quatre traits spécifiques énumérées toute à l’heure précédemment, et notamment une image dont le parcours de la genèse peut être justifié et reproduit à partir des paramètres expérimentaux ou des modèles mathématiques. Deux autres types d’images sont utilisés dans la littérature scientifique : la première est l’image de statut artistique, image produite par un artiste, qui se situe dans une tradition artistique et qui est utilisée par les scientifiques notamment dans le genre de la vulgarisation savante. La deuxième est la vue d’artiste, produite par des scientifiques, par exemple des astrophysiciens graphistes qui travaillent pour la NASA. Si nous nous sommes consacrée dans les pages précédentes aux vues d’artiste, nous nous consacrerons à présent plus spécifiquement à l’image artistique tout court.

En général, l’image artistique peut être publiée pour signifier le fait que les modèles d’espace expérimentés par les scientifiques peuvent avoir eu comme source d’inspiration une organisation spatiale déjà exploitée par des artistes. Certains scientifiques déclarent cette source. Pensons banalement à la Renaissance où Copernic avait été influencé par les artistes et savants italiens quant à la représentation de l’espace tridimensionnel, qu’il incorporait dans son système astronomique en transformant la fenêtre de Brunelleschi en une fenêtre mouvante (en concevant la terre en mouvement). L’application de la perspective à la vue humaine du ciel lui permit de déterminer la structure du cosmos et les relations parmi ses constituants, ainsi que de calculer la distance entre les étoiles. La perspective est d’ailleurs un système qui permet de construire une commensurabilité entre des objets de taille et de distance divers.

Figure 4 : M.C. Escher, Study of Stars, wood engraving, 1948

Figure 5 : M.C. Escher, Symmetry Watercolor 78, watercolor/colored pencil, 7 7/8 x 7 7/8, 1950

Escher est bien sûr considéré comme un artiste, mais ces images résultent d’expériences de la géométrie hyperbolique et sont devenues des images qui ont posé des problèmes mathématiques et qui ont fait évoluer la réflexion de la géométrie. Voyons comment.

Les modèles d’univers qui sont incarnés par cette deuxième image d’Escher sont appelés wraparound models : ces modèles utilisent des cubes ou des parallélépipèdes pour créer un espace toroïdal, leur propriété principale étant de se fonder sur des symétries. Ces symétries sont réalisées par des groupes d’holonomie selon lesquels les points correspondant à chaque face sont collés entre eux d’une manière telle que l’espace physique résulte d’un processus complexe de repliement sur lui-même. Ces modèles mathématiques changent beaucoup de choses en astronomie : il ne s’agit plus de penser qu’à chaque point de la lumière observable correspond une étoile spécifique, mais de penser que chaque corps céleste est représenté par un certain nombre d’images fantômes ou mirages gravitationnels (ghost images), ce qui veut dire que ce que nous voyons n’est pas le ciel comme il est, mais un croisement et une multiplication d’images de l’univers, à plusieurs distances et points de vue, superposées les unes aux autres (Figure 6).

Figure 6 : Jeff Weeks, Espace dodécaédrique de Poincaré (Luminet, 2009, p. 12)

Cette image illustre l’espace dodécaédrique théorisé par Poincaré, composée par un mathématicien collaborateur de Luminet, Jeff Weeks. Il s’agit d’une vue simulée, depuis l’intérieur de l’espace dodécaédrique, dans une direction arbitraire, calculée par le programme Curved Spaces et montrant des images multiples de la Terre obtenues par mirage topologique. Nous voyons ici les simulacres de la Terre, à des distances différentes des angles des parallélépipèdes. L’effet est comparable mais non identique à ce qu’on pourrait voir de l’intérieur d’un parallélépipède dont les faces internes sont recouvertes de miroirs, où les reflets se croisent et se multiplient. Cette méthode cristallographique a été développée pour visualiser la distribution en 3D de certaines sources de lumière : les corrélations visualisées signalent des répétitions de patterns comme dans les cristaux. Imaginons une source lumineuse à partir de notre position d’observation, immergée dans cette structure : la lumière émise devant nous croise la face du parallélépipède derrière nous et réapparaît dans la face opposée devant nous, et nous pouvons avoir, en regardant devant nous, une vision de ce qui se situe derrière nous. Même chose pour la gauche et la droite, pour le bas et le haut.

Un observateur qui vit dans l’espace dodécaédrique de Poincaré a l’illusion de vivre dans un espace 120 fois plus vaste, fait de dodécaèdres donnant un effet de carrelage. Cet espace tessellé à la manière d’un mosaïque ‑ le terme qui le décrit en anglais est tessellation ‑ résulte des transformations mathématiques qui ont été utilisées pour coller les angles par translation et formant des groupes de symétries.

Un minéralogiste russe Fedorov en 1891 avait démontré que les groupes de symétries qu’il fallait pour carreler régulièrement un plan étaient en nombre de 17, et en 1922 un archéologue, Andreas Speiser, s’aperçut que ces 17 groupes de symétries avaient été découverts empiriquement 400 ans auparavant dans les arts décoratifs des mosaïques de l’Alhambra à Grenade (Figure 7) :

Figure 7 : Particulier des mosaïques de l’Alhambra à Grenade : configuration à “pajarita” (cocotte en papier) dans la partie basse des murs du patio de los Arrayanes.

Les patterns résultaient des combinaisons de symétries simples ou complexes et toutes réductibles aux 17 groupes de symétries mathématiquement identifiés très longtemps après par le minéralogiste russe Fedorov, qui en a donné une description mathématique exhaustive.

En revenant maintenant à l’image d’Escher vue auparavant (Figure 5), on peut affirmer que cette image de statut artistique non seulement hérite son iconographie des groupes des symétries institutionnalisés en mathématiques, qui ont à leur tour recueilli l’héritage d’une expertise due aux arts décoratifs, mais que cette série d’images de pavage d’Escher ouvre elle-même un nouveau champ de la géométrie, appelé ensuite la théorie des groupes de symétries polychromes : les couleurs des patterns n’avaient pas été prises en compte par la théorie des groupes de symétries du minéralogiste russe Fedorov. Après Escher et sa série d’images The Circle Limit (1958), ces patterns colorés ont été étudiés par Donald Coxeter, un de plus important géomètre du XX^e siècle.

Par rapport au passage de statut de l’image artistique à celui de l’image scientifique, on peut donc affirmer que ces images d’Escher ont posé des problèmes mathématiques en faisant ainsi évoluer la réflexion de la géométrie : c’est bien la relation entre les couleurs et les symétries qui a ouvert de nouvelles pistes de réflexions, et cela grâce aux expériences d’un artiste.

3. Texte verbal vs. représentation visuelle ou mathématisation VS. visualisation ?

Nous voudrions terminer en prenant brièvement en considération la troisième question concernant la frontière entre ce qui relève du textuel et ce qui relève du visuel.

La résistance qu’on éprouve à éliminer cette distinction entre verbal et visuel en sciences du langage cache une distinction plus enracinée encore dans notre culture, celle qui existe entre digital et analogique : dans le cas du verbal, les unités sont censées être facilement identifiables car disjointes, alors que dans le cas des représentations visuelles et notamment de l’image, les traits sont difficilement digitalisables et difficilement identifiables. Cela a entrainé aussi une méfiance envers la possibilité de concevoir une syntaxe de l’image fixe.

Il nous semble que c’est justement cette séparation entre analogique/digital et entre visuel/verbal que la sémiotique greimassienne a essayé de dépasser en montrant que ce n’est pas l’élément isolé ‑ les traits visuels ou les graphèmes ‑qu’il faut prendre en compte lors de l’analyse : la taille pertinente dans les deux cas est suprasegmentale et discursive, l’organisation discursive étant irréductible à l’addition des traits qui la composent.

Nous voudrions porter brièvement l’attention sur une autre distinction qui calque celle entre analogique et digital et qui est transposable à d’autres distinctions plus proches du domaine qui nous intéresse ici : celle entre visualisation et mathématisation, qui nous semble plus appropriée que celle entre visuel et verbal du point de vue d’une heuristique sémiotique. La distinction visuel/verbal est à notre sens moins heuristique, puisqu’elle relève de la substance de l’expression des langages, mais elle n’est pas forcément utile du point de vue de la signification des langages. Mettons donc ces deux distinctions à l’épreuve de ce que nous avons affirmé du diagramme toute à l’heure : à travers la distinction entre visuel et verbal, on ne pourrait pas distinguer le diagramme des graphiques et des schémas ; à travers la distinction entre visualisation et mathématisation on pourrait arriver à comprendre ce qui distingue un diagramme d’un graphique : en fait le graphique n’est pas censée être manipulable et il n’est donc pas un « flat laboratory », comme l’est par contre le diagramme. Mais cette dernière distinction permet surtout d’affirmer que le fonctionnement diagrammatique comprend d’autres configurations imageantes que des simples schémas, à savoir des images comme on l’a vu toute à l’heure avec les visualisations mixtes, qui rendent pertinente la relation entre perception et généralisation, entre enracinement spatial et transposabilité, entre observabilité et imagination. L’image mixte des trous noirs a permis des expériences de la pensée : à travers plusieurs étapes et manipulations on est arrivée à une image calculée qui est une image des trous noirs logiquement possibles. C’est ce processus de pluralisation des possibles, déployés à travers une visualisation manipulable, que nous appelons processus diagrammatique à l’intérieur de l’image scientifique.

Conclusions

Par rapport aux graphiques et aux schémas, le diagramme a des spécificités importantes, car il ne fait plus partie d’un statut textuel ‑ et j’entends ici « textuel » selon la définition de la sémiotique greimassienne, voire en tant que configuration de sens fermé. En fait le diagramme fonctionne comme une icône de relations qui trouve une exemplification dans un scénario qui dépasse les attributions de signification déjà cristallisés.

En ce qui concerne notre enquête sur l’image diagrammatique en tant qu’image nécessaire, on peut enfin affirmer que les images artistiques autant que les images scientifiques manifestent une certaine nécessité existentielle ; dans le cas de l’image artistique il s’agit d’une nécessité qui est interne à sa configuration : il s’agit d’une nécessité qui sera figée ‑ au sens de sacralisée ‑ par le monde de l’art qui en fera une œuvre. Cette nécessité de l’image artistique dérive aussi d’une densité syntaxique et sémantique de sa topologie (aucun trait ne peut être déplacé faute de compromettre toute la signification de l’image) ; en revanche, l’image scientifique manifeste une nécessité due non pas à elle-même, mais à la contrôlabilité de ses paramètres de production et aux règles de transformation et manipulation qui ne lui sont pas internes, mais dépendant d’une chaîne d’opérations qui l’ont précédée. Dans le cas de l’image scientifique entendue en tant que support d’expérimentation (visualisation mixte), elle attend d’être rendue opérationnelle et ensuite transformée en d’autres images (elle est un « texte d’instructions »). Sa caractéristique principale est donc d’être produite par des paramètres contrôlés et de produire d’autres images qui peuvent trouver en elle une (partielle) justification. Mais comme on vient de le voir dans la théorie peircienne du diagramme, ce n’est pas la créativité tout court qui distingue l’image scientifique de l’image artistique : il faut également concevoir dans le cas du diagramme mathématique l’élément créateur, même si réglé par des procédures et des codes de transformation.