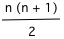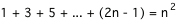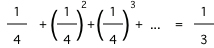Vers une classification diagrammatique

1. Introduction

Beaucoup d’articles consacrés au thème des images commencent par souligner le fait que nous sommes entourés tous les jours et partout par celles-ci : nous trouvons des photographies dans les journaux, des graphiques dans les revues scientifiques, des indications visuelles dans le métro, des icônes au supermarché ou même sur la petite machine à café qui se trouve sur notre lieu de travail. Le sentiment que nous pouvons éprouver en raison de cette présence en tous lieux des images est d’être submergés par elles, sans qu’il y ait des critères généraux permettant d’établir des distinctions entre différents types ou différentes fonctions des images. Pour cette raison, il paraît nécessaire de proposer un cadre d’analyse général pour les images et leurs utilisations très hétérogènes.

Si nous restreignons notre attention aux images utilisées dans les sciences, nous rencontrons encore des difficultés lorsqu’il s’agit de définir avec précision quelle image est scientifique : existe-t-il des caractéristiques communes à toutes les images scientifiques ? En fait, l'étiquette « image scientifique » peut bien être appliquée aux schémas, aux graphiques, aux microphotographies, et plus généralement aux images qui sont publiées dans les revues en vue de diffuser des résultats scientifiques, ainsi qu’aux images utilisées dans le laboratoire pour la recherche et la communication entre scientifiques. Y-a-t-il donc des conditions nécessaires et suffisantes permettant de décider en principe qu’une certaine image est une image scientifique ? Est-il possible de considérer une image en tant qu’image scientifique en dehors d’un contexte théorique et/ou historique particulier ? Entre parenthèses, à certains égards, ce type de questions s’apparente aux questions qui peuvent se poser sur les critères nécessaires et suffisants pour distinguer une image artistique de celles qui ne le sont pas : on se situe dans un de ces champs de recherche où les sciences et les arts semblent se rapprocher les unes des autres.

Il faut donc revenir à la question d’une définition claire et en même temps pas trop générale de ce qu’il est légitime d’appeler « image scientifique ». Si on se renseigne dans la littérature, on trouve qu’il n’existe de consensus, ni sur ce qui rend les images scientifiques différentes du langage, ni sur les raisons qui expliquent l’avantage que confère leur utilisation par rapport à celle du langage dans certains contextes. À l’ensemble des images scientifiques appartiennent sans doute les diagrammes, les graphiques et toutes les différentes formes d’expression et de communication utilisées dans le laboratoire ainsi que dans la diffusion des résultats parmi les scientifiques et auprès du grand public. Pourtant, il n’existe pas non plus de méthodologie clairement définie pour étudier ces visualisations. En effet, une étude portant sur les diagrammes et sur les images présente de difficultés parce qu’elle se situe à la rencontre de différentes théories ; d’un côté, on a besoin d’une théorie relative à la capacité des images à transmettre de l’information, et de l’autre, on cherche à développer une théorie de l'interprétation des signes et des propriétés du langage. Toutefois, dans les deux cas, on ne peut pas définir une image scientifique sans tenir compte du rôle qu’elle joue dans notre système général des connaissances.

Après avoir pris acte du fait que nous sommes submergés par un flot d’images, les articles standards prenant ces dernières pour thème d’investigation mentionnent pour la plupart la célèbre - et plutôt galvaudée - maxime chinoise selon laquelle « une image vaut dix milles paroles ». Cette maxime exprime une idée de sens commun, mais celle-ci est potentiellement trompeuse, car les images et les mots ne sont pas des systèmes de représentation interchangeables. Il convient plutôt de les voir comme utilisés de façon complémentaire en fonction du contexte et de la tâche qu’on leur assigne. Il n’y a ni raison, ni preuve autorisant à affirmer que la pensée humaine exploite dans chaque situation cognitive un seul canal ou une seule modalité : au contraire, il est évident qu’elle active constamment des systèmes de représentation hétérogènes qui interagissent entre eux, et qui peuvent être visuels, spatiaux, linguistiques, ainsi que visuels/spatiaux ou linguistiques/spatiaux. En fait, les systèmes sont si entrecroisés que l’opposition visuel d’un côté, linguistique de l’autre perd tout intérêt.

Une autre conséquence est que si ces systèmes sont complémentaires, alors il n’est pas vrai que les images sont en un certain sens plus « directes » que le langage. Selon les positions théoriques adoptées par certains auteurs, la compréhension des images est plus immédiate parce que ces dernières transmettraient l’information directement à travers la vision, sans nécessiter de règles intermédiaires qu’il faudrait au préalable apprendre. Mais cette intuition est fausse : en fait, voir une image n’est pas suffisant pour lui conférer une signification, parce que le « voir » qui nous intéresse est plutôt le résultat d’un parcours culturel complexe, à certains égards très similaire à celui de la lecture.

Dans cet article, je présenterai les lignes générales pour la classification diagrammatique que je propose. Je qualifie cette classification de « diagrammatique », parce que, comme je le montrerai, elle est pensée comme un cadre général valant pour les diagrammes et en même temps, elle est elle-même présentée sous la forme d’un diagramme. Pour ce qui concerne mon choix de parler de diagrammes plutôt que d’images, je considère l’étiquette « diagramme » comme la plus générale : un diagramme est une figure bidimensionnelle, la bi-dimensionnalité jouant un rôle spécifique dans la transmission de l’information. Je discuterai de la manière dont l’espace et la configuration spatiale importent dans la compréhension et l’utilisation d’un diagramme.

2. Le cas des figures et diagrammes en mathématique

Avant d’introduire ma classification, je vais présenter d’abord l’utilisation de diagrammes et des figures en mathématiques en particulier. Je soutiens que le cas des mathématiques montre bien la complexité de l’emploi de ces instruments visuels. Je discuterai ensuite, en adoptant une perspective plus générale, des avantages qu’offre le raisonnement par diagrammes et images dans le cadre du discours scientifique.

Malgré la présence massive des diagrammes et des figures en mathématiques, la philosophie des mathématiques du siècle passé s’est plutôt consacrée à l'évaluation et à l’étude de l’apport du langage formel dans ce domaine des sciences. Il y a bien sûr des raisons historiques permettant de comprendre le choix de cette approche, mais je ne développerai pas ce point ici. Je dirai simplement que l’attitude consistant à ne pas s’occuper du raisonnement diagrammatique en mathématiques est une attitude erronée qui ne rend pas compte des aspects plus dynamiques, et d’une certaine façon plus intéressants car plus créatifs, des mathématiques. La considération des manières dont les mathématiciens font référence très souvent aux schémas et aux visualisations est cruciale pour l'épistémologie des mathématiques et pour déterminer ce qu’on peut appeler la pratique - ou les pratiques - des mathématiques.

Ma thèse principale est que le format dans lequel une certaine information est représentée détermine le type de raisonnement qui sera effectué sur cette information-là, à travers une manipulation de la représentation en question. En d’autres termes, il existe une connexion fondamentale entre la représentation de l’information et la résolution du problème. Avant d’aller plus loin, je débuterai par une clarification de mon usage du terme « représentation ». Je me sers de cette étiquette d’une façon très large : « représentation », dans ce contexte, signifie tout simplement « signe sur la page qui possède une signification ». En ce sens, une formule linéaire ou un diagramme sont des représentations. Ce lien entre format de l’information et type de raisonnement effectué dans la recherche et la résolution du problème n’est pas un attribut distinctif des diagrammes utilisés dans les mathématiques, mais concerne aussi d’autres catégories de diagrammes, comme je le montrerai en introduisant la classification que je propose.

Deux aspects fondamentaux caractérisent les diagrammes et les figures et leur permettent de transmettre des informations. Tout d’abord, les diagrammes exploitent les principes de la perception classique des objets tels que les Gestalts, ainsi que leurs interactions possibles. En d’autres termes, quand on perçoit un diagramme, on capte certaines relations spatiales et topologiques entre ses différents éléments.

Considérons par exemple Fig.1.

Fig.1

Dans cette figure, le sujet perçoit une série de cercles de différentes couleurs - blancs et noirs - et reconnaît qu’ils sont configurés dans un carré. De surcroît, une moitié de ce carré est remplie par les cercles noirs, et l’autre moitié par les cercles blancs. Il y a une ligne qui divise les deux moitiés.

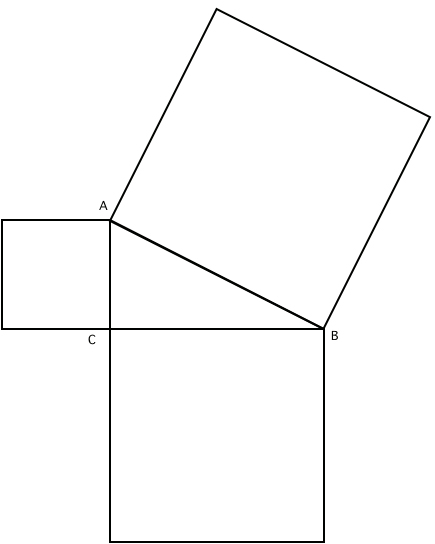
Considérons maintenant la Fig.2.

Fig.2

Dans ce cas, le sujet perçoit certaines relations spatiales, mais cette fois, les relations pertinentes sont continues plutôt que discrètes. La figure contient bien sûr ce que le sujet reconnaît comme étant un triangle et trois carrés, mais il faut aussi remarquer que ces trois carrés ont chacun un côté en commun avec le triangle. Dans la figure, certaines lettres - A, B, et C - apparaissent également, et elles sont placées à des endroits spécifiques, juste à côté des sommets du triangle.

À ce niveau-là, si on veut utiliser une étiquette afin de définir de quelle façon cette figure transmet cette information au sujet, on peut dire que la figure est une icône : elle montre certaines relations spatiales et une configuration spatiale spécifique que le sujet est capable de capter et de reconnaître. Mais cela ne suffit pas pour expliquer comment la figure est utilisée dans le raisonnement mathématique en vue d’arriver à une conclusion à partir des prémisses initiales. En fait, la détection des propriétés spatiales de la figure doit être intégrée à la considération d’un contexte de référence que le sujet présuppose, plus ou moins consciemment.

Considérons encore une fois nos exemples. La Fig.1 représente une des démonstrations visuelles du théorème de la somme des premières nombres naturels, qui selon le théorème correspond à

La Fig.2 représente les éléments qui figurent reliés les uns aux autres dans le célèbre théorème de Pythagore. Ce type de connaissance ne dépend pas - ou, à vrai dire, ne dépend pas seulement - des relations spatiales captées, mais exige la familiarité du sujet avec un ensemble de concepts qui sont nécessaires pour la compréhension correcte de la figure. A ce niveau donc, le diagramme est interprété et devient ainsi un symbole. La figure n’est pas simplement un véhicule d'information spatiale, elle transmet aussi une information conceptuelle.

Par conséquent, à partir de ces exemples simples, je propose qu’on considère que les diagrammes en général sont assujettis à deux types de contraintes. A un premier niveau, ils sont des icônes, c’est-à-dire qu’ils présentent certaines caractéristiques spatiales, et donc ils possèdent des contraintes perceptives ; à un deuxième niveau, ils sont des symboles, c’est-à-dire qu’ils évoquent la connaissance d’un contexte de référence pour leur lecture correcte, et donc ils possèdent des contraintes conceptuelles. Je ne veux pas soutenir que ces deux niveaux sont clairement distincts ; au contraire, les deux niveaux sont en interaction continue : le sujet voit des relations spatiales et les interprète ainsi qu’il peut donner des nouvelles interprétations et par conséquent « voir » une nouvelle configuration dans la figure.

Pour résumer, mon intention était ici de montrer comment dans les mathématiques, les diagrammes ne sont pas simplement « vus » par le sujet. Il faut bien comprendre que le sens de « voir » ici correspond à une activité cognitive complexe qui n’est pas directe, mais passe par deux niveaux de contraintes. Le sujet doit sélectionner d’abord les relations spatiales pertinentes, puis le cadre conceptuel approprié pour la tâche. Les diagrammes et les figures en mathématiques révèlent leurs multiples caractéristiques : d’un côté, on a la représentation visuelle et spatiale, c’est-à-dire l'objet diagramme ; de l’autre, on trouve le sujet qui utilise cette représentation et qui doit être au courant de ces contraintes perceptives et interprétatives. Tout cela se fait jour dans le cadre de la tâche particulière pour laquelle la figure est ou a été conçue.

Pour l’instant, je ne vais pas discuter de manière plus approfondie ces trois aspects que je viens de présenter - diagramme, sujet utilisateur, tâche. On les retrouvera cependant dans la classification que je proposerai dans la suite de l’article. Dans la prochaine section, je vais en revanche continuer mon parcours d’introduction à l’utilisation des diagrammes : je sortirai cette fois du contexte spécifique des mathématiques, et je montrerai ce qui se passe avec les diagrammes et les images quand on considère leurs usages dans le domaine plus général des sciences et du traitement de l’information.

3. Les diagrammes comme externalisations non linguistiques

Je soutiens que le choix d’utiliser un diagramme comporte généralement des avantages. Les hypothèses que je prends en considération pour arriver à ces conclusions sont les suivantes.

Tout d’abord, on trouve que dans certaines tâches, les diagrammes sont plus avantageux que les représentations linguistiques. Considérons par exemple le cas des nombreuses représentations spatiales non-linguistiques qui sont couramment utilisées pour afficher des variables qui ne sont pas spatiales à l’origine. Par exemple, on a des « arbres » qui peuvent décrire des relations de parenté, ou des « hiérarchies » qui montrent des relations de dépendance, des « graphiques » qui peuvent signaler le changement d’une certaine variable par rapport au temps, et finalement des « icônes » qui donnent des instructions ou des indications sur les manières dont il faut se comporter. Admettons que tous ces types d’information puissent être donnés à travers le langage naturel, et imaginons qu’on décide d’utiliser la « traduction linguistique » de ce que ces diagrammes expriment. L’intuition est que le choix d'éliminer la configuration spatiale va représenter un manque à gagner dans la recherche ainsi que dans l’extraction, et même dans la compréhension, de l’information que nous intéresse.

De surcroît, les diagrammes représentent également un avantage cognitif par rapport à la référence au calcul mental, précisément parce que les diagrammes sont des outils extra-mentaux qui permettent d'alléger la charge cognitive exigée de la mémoire de travail. Plusieurs études soutiennent que certains problèmes cognitifs sont résolus plus rapidement, plus facilement et de manière plus fiable, quand la recherche de l’information pertinente et les actions menées sur elle ne sont pas seulement effectuées mentalement, mais prennent également appui sur des objets extérieurs (Larkin et Simon, 1995). Considérons par exemples les avantages résultant de l’emploi des cartes, comme aussi des tableaux, des listes ou des images schématiques contenues dans les manuels scientifiques.

Pour préciser ce point : les diagrammes, comme je l’ai déjà souligné au début de cet article, ne sont pas à penser du tout en opposition aux représentations linguistiques. De la même façon, ils ne sont non plus en opposition avec les représentations mentales. Au contraire, la recherche sur les diagrammes est par nature interdisciplinaire. D’abord, ils demandent une théorie sur la communication humaine. On a trois éléments dont il faut considérer le rapport : les diagrammes extérieurs, le sujet qui les utilise, et en fin la tâche et le contexte de résolution de problème concerné à chaque fois. En plus, quel est le rapport entre ces trois éléments et le langage naturel ? Ensuite, les diagrammes concernent également une théorie du fonctionnement de la mémoire et du raisonnement, ainsi que du calcul mental et de l’organisation de l’information. Une étude consacrée aux diagrammes peut apporter une contribution à l’étude relative aux représentations internes en jeu quand on raisonne « spatialement ». Enfin, les diagrammes présentent également un intérêt pour une théorie sur l’art (Goodman, 1968). En effet, ils sont des représentations externes, mais ils ne sont pas des images picturales ou du moins, ils ne sont pas conçus comme tels. Quelles sont les différences et les analogies que l’on peut établir entre diagrammes et images picturales ?

Si tout ce qui précède est vrai, alors on peut bien penser que les diagrammes constituent un domaine de recherche potentiellement capable de mettre en communication ces trois différentes théories qui représentent trois volets différents et cruciaux de notre cognition.

4. Les raisons et les variables de la classification

Le but de cet article est de proposer une classification diagrammatique. Vu les éléments que j’ai introduit jusqu’ici dans mon argumentation, l’idée est qu’une classification peut représenter une première étape utile ou même nécessaire pour étudier ce type de représentations. Je soutiens que cette classification présente deux avantages.

D’abord, elle reflète le contexte de référence complexe que je viens de mettre en relief et qui va au-delà de la dichotomie langage d’un côté, vision de l’autre. Cette dichotomie est en réalité trompeuse car les représentations ne sont jamais totalement linguistiques ou totalement visuelles. Comme on l’a vu dans le cas des figures et des diagrammes en mathématiques, ce qui compte pour être capable d’utiliser une figure ou un diagramme n’est pas le fait que cette figure ou ce diagramme soit visuel. Il importe plutôt de connaître les contraintes auxquelles cette figure ou ce diagramme est assujetti. Ces contraintes ne sont pas seulement perceptives, mais également interprétatives/symboliques.

La classification que je propose reflète par ailleurs le passage d’une approche « structurelle » des diagrammes à une approche qui est plutôt liée au traitement des données et de l’information. En fait, la classification est conçue pour répondre à la seule question pertinente sur les diagrammes, qui n’est pas « Qu’est-ce qu’est un diagramme ? », mais plutôt : « Comment peut-on utiliser un diagramme ? ». Pour parler de raisonnement diagrammatique, il faut aussi considérer le troisième aspect que j’ai souligné dans le cas des mathématiques, c’est-à-dire la tâche particulière pour laquelle le diagramme est constitué et proposé à l’appréhension du sujet.

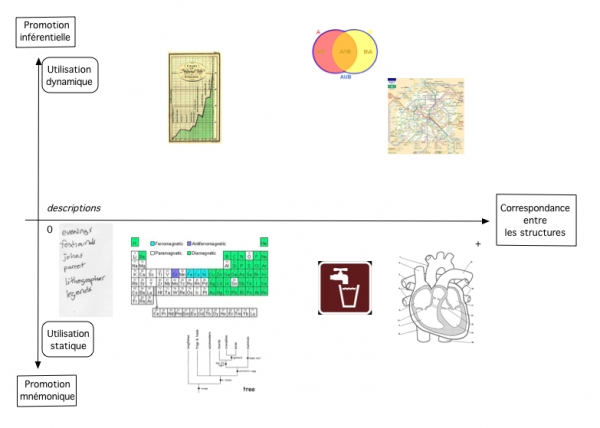
Dans la classification, j’ai choisi de me concentrer sur une distinction simple entre deux types d’utilisation possible des diagrammes. Ces types d’utilisations se trouvent sur l’axe vertical de la classification, comme montré dans la Fig.3.

Fig.3

L’hypothèse à l’origine de la définition de cet axe vertical est que les diagrammes peuvent être utilisés de deux manières : une utilisation statique - en bas - et une utilisation dynamique - en haut. L’utilisation statique vise à transmettre et à obtenir des données à partir du diagramme, et pour cette raison, elle a comme but de promouvoir la mémoire. Cette caractéristique de certains diagrammes exprime le fait que la disposition spatiale est pertinente pour l’extraction et le stockage de l’information : dans l’utilisation statique, l’utilisateur « lit » l’objet diagramme, et cet objet active sa mémoire. A l’autre extrémité, l’utilisation dynamique vise à tester et à confirmer une hypothèse et à encourager la production d’inférences, et pour cette raison elle a comme but une promotion inférentielle ; dans l’utilisation dynamique, le sujet utilise l’information contenue dans l’objet diagramme comme prémisse pour dériver de nouvelles conclusions. Ce deuxième processus est plus dynamique que le précédent parce que normalement, dans ce cas, le sujet est « invité » à modifier l’objet diagramme à travers des actions qui peuvent être pragmatiques ou épistémiques. Suivant la définition de Kirsh et Maglio, une action pragmatique est une action dont la fonction est de conduire l’agent vers son objectif physique (Kirsh et Maglio, 1994). Par exemple toutes les actions qui sont effectuées dans l’espace physique ou social pour parvenir à un certain but sont des actions pragmatiques. Mais les sujets effectuent aussi des actions épistémiques, qui sont des actions physiques dont la fonction est d'améliorer la cognition. Cela peut revêtir trois formes : en réduisant la charge de la mémoire du travail, c’est-à-dire la complexité spatiale ; en réduisant le nombre de pas impliqué par la computation mentale, c’est-à-dire la complexité temporelle ; ou finalement en réduisant la probabilité d’erreur, c’est-à-dire la faillibilité. L’exemple utilisé par les deux chercheurs est le jeu vidéo Tetris, mais cette distinction peut s’appliquer aussi au cas des diagrammes en général, étant donné que ceux-ci peuvent également être manipulés et modifiés en vue de trouver la solution de la tâche pour laquelle ils ont été créés.

Je reviendrai par la suite sur cet aspect de manipulation des diagrammes. Pour l’instant, je continue avec la classification et je vais considérer l’axe horizontal, qui on voit dans la Fig.4.

Fig.4

Sur l’axe horizontal se trouve la correspondance entre la structure du diagramme, ou plus généralement la représentation externe, et la structure des données à représenter. Cette dimension est un continuum entre les cas où cette correspondance est absente, comme dans les descriptions linguistiques, où la relation entre structure de la représentation et structure des donnés est arbitraire, et ceux où cette relation est manifeste et se rapproche de l’isomorphisme, comme c’est le cas avec les images scientifiques. Entre ces deux cas extrêmes, on trouve toute une série de diagrammes et d’images pour lesquelles ce rapport est modulé différemment, et il existe une correspondance plus ou moins grande entre la structure de la représentation et la structure des données.

Pour fournir des exemples concrets, dans la partie inférieure de la classification - donc, parmi les diagrammes qui sont utilisés comment aide pour la mémoire - on trouve les listes, les tableaux, les arbres, les icônes et les images schématiques. Ces diagrammes sont caractérisés par une correspondance de plus en plus grande entre les deux structures. Dans la partie supérieure de la classification - donc, parmi les diagrammes qui sont utilisés comment auxiliaire inférentiel - on trouve les graphiques, les cercles de Venn et les cartes.

Il faut souligner deux aspects de cette classification. D’abord, je considère qu’il y a des représentations qui peuvent être utilisées d’une façon statique aussi bien que d’une façon dynamique. Cela dépend de la tâche particulière à réaliser. Examinons par exemple le cas des cartes. Le sujet peut bien utiliser une carte pour se souvenir et mémoriser l’emplacement d’un certain endroit et ses relations avec les zones environnantes. Je dirai qu’il utilisé donc la carte d’une façon statique. A l’inverse, si le sujet cherche un parcours et veut trouver comment arriver d’un endroit à un autre, alors il doit d’une certaine façon « manipuler » la carte, l'orienter dans la direction appropriée, former des inférences par rapport aux distances à parcourir ou aux transports à utiliser.

Deuxièmement, je répète que les diagrammes dans la classification diffèrent des images entendues au sens large. En fait, la classification ne comprend pas des objets strictement picturaux, mais de vrais artefacts qui ont étés conçus pour assister la mémoire et pour promouvoir les inférences. Par conséquent, le sujet peut bien donner aussi un jugement esthétique par rapport à certains de ces diagrammes, mais s’il le fait, il ne va pas reconnaître la fonction intrinsèque de ces diagrammes : reproduire et organiser une certaine information.

5. Les diagrammes « constructifs »

Considérons maintenant dans le détail la seconde fonction des diagrammes selon la classification. Cette fonction que j’ai appelé « promotion inférentielle » est plutôt remplie par les représentations utilisées de façon dynamique.

Je formule ici plusieurs hypothèses. La première hypothèse est que les diagrammes qui promeuvent les inférences sont compris seulement lorsqu’ils sont correctement manipulés. C'est-à-dire que le sujet montre qu’il connaît l’utilisation de l’artefact en question seulement quand il montre qu’il est capable de le manipuler correctement. De cette façon, les diagrammes sont très similaires à d’autres outils. Leur fonction - celle pour laquelle ils ont été créés - est d’être utilisés, et pour les utiliser, il faut savoir comment ils fonctionnent et quelles actions il faut accomplir sur eux afin de les faire fonctionner.

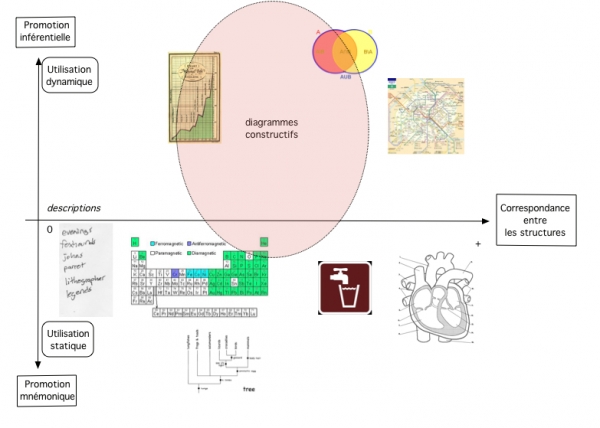
La deuxième hypothèse est qu’il n’est pas vrai que les diagrammes dévoilent l’information instantanément comme certaines études semblent le suggérer, en disant que l’information est simplement et directement extraite d’un diagramme au travers d’une sorte de « coup d’œil ». Par contre, les diagrammes de ce type répondent aux règles de construction, et ils sont construits étape par étape. Conséquemment, le contenu de ces diagrammes est déterminé par les instructions qu’ils fournissent au sujet pour organiser l’espace du problème. Pour cette raison, je définis ces diagrammes comme étant constructifs. Les diagrammes constructifs occupent une portion de la classification plus ou moins au centre de l’axe horizontal, et surtout dans l’espace en haut de l’axe vertical, comme montré dans la Fig.5.

Fig.5

Avant de proposer des exemples de diagrammes constructifs, je vais clarifier ce que « diagramme constructif » signifie.

Le terme m’a été suggéré par l’expression de Maynard, « dessins constructifs » (en anglais, « constructional drawings »), qui fait référence au travail de Booker sur les dessins en ingénierie (Maynard, 2005 ; Booker, 1963). L’expression « dessin constructif » renvoie à un certain type de dessins qui n’ont pas été vraiment pris en compte dans les études les plus récentes portant sur les images. En effet, selon Booker, les études sur les dessins se sont occupés plutôt des dessins marqués sur le papier ou sur la toile, et ils ont presque totalement ignoré ce qu’aujourd’hui, on appelle « dessins détaillés » (« detail drawings »), c’est-à-dire des dessins réalisés directement sur la pierre ou sur le bois, et non sur le papier.

Le personnage au centre de la Fig.6 illustre l’activité de création d’un tel dessin constructif. L’illustration est extraite du Recueil des Planches de l’Encyclopédie de Diderot et d’Alembert (du premier volume, « Architecture, Maçonnerie »). Ce type de dessin présente un intérêt pour ma classification parce qu’ils ne sont pas des dessins picturaux - depictive, en anglais - mais sont donnés plutôt en tant qu’outils pour calculer et mesurer, et donc comme outils cognitifs. Ils peuvent - et dans une certaine mesure, ils doivent - être modifiés, reconsidérés, pré-planifiés. Leurs formes doivent être comprises comme des opérations qui ne sont pas visibles dans le produit final : c’est parce que le sujet est capable de reproduire, de dessiner ces dessins tout comme il doit aussi être capable de comprendre le résultat à quoi ces dessins font référence.

Sur ce point, Ferguson a soutenu que jusqu’à la deuxième moitié du XX^e siècle, l'enseignement des dessins techniques dans les écoles d’ingénierie passait par l’enseignement des techniques permettant de tracer ces dessins. En fait, la compréhension de la nature des matériaux et des machines reposait sur l'expérience dans le laboratoire. Comme suggéré par l’auteur, la formation de Filippo Brunelleschi, de Francesco di Giorgio, et de Léonard de Vinci incluait l’apprentissage de la préparation et de l’utilisation des matériaux requis pour dessiner, peindre, sculpter la pierre et le métal. Leur connaissance était basée sur les observations sensorielles et ils étaient guidés par des maîtres qui montraient aux élèves l’objet de la recherche. (Ferguson 1992, p. 153).

Fig. 6. Gravure extraite de l’Encyclopédie de Diderot et d’Alembert (18^e siècle)

Revenons donc aux diagrammes constructifs de ma classification. Mon hypothèse est que quand on voit ces diagrammes, on voit une pratique. C’est-à-dire que le sujet comprend ces diagrammes seulement s’il connaît la procédure correcte à appliquer sur ceux-ci. Bien sûr, il y a plusieurs procédures susceptibles d’être appliquées, et plusieurs manipulations peuvent être obtenues. Pourtant, si on connaît la procédure correcte, celle-ci nous donnera parmi toutes les manipulations possibles, celles qui sont appropriées par rapport à la tâche.

Je tiens à souligner que cette notion de manipulation ou de procédure nous mène au-delà des dichotomies qui ont traditionnellement animé le débat, comme la dichotomie langage/vision évoquée au début de l’article, ou celle qui oppose syntaxe et sémantique, que j’ai choisi de ne pas considérer dans ma classification, ou celle qui existe entre interne et externe - est-ce que le diagramme est représenté dans notre esprit ou est-il sur le papier ? - ou encore celle qui distingue radicalement mental et matériel - est-ce que le raisonnement diagrammatique se produit dans l’esprit ou dans le monde externe ? Je suggère que si on regarde les procédures que les sujets sont capables d’appliquer une fois qu’ils ont appris la pratique, la dualité du raisonnement diagrammatique entre objet-diagramme et sujet-utilisateur est recomposée. Dans le même temps, on a aussi réussi à conserver les aspects plus pragmatiques et à considérer la tâche particulière accomplie ou à accomplir. De surcroît, cette pratique n’est pas apprise par le sujet en mémorisant un ensemble de règles explicites, mais par la familiarisation acquise avec les manipulations réalisées.

Si les diagrammes constructifs invitent donc leur utilisateur à mener certaines opérations sur eux-mêmes, cela signifie que ces diagrammes révèlent les informations qu’ils contiennent de manière globale et synthétique, mais cependant pas en un seul instant. Ces deux aspects - façon globale et synthétique de représenter l’information, et information communiquée en un seul instant - ne sont pas équivalents. En fait, les diagrammes inférentiels sont donnés et construits étape par étape. Le message qu’ils contiennent est un message relatif aux procédures d’organisation spatiale, une organisation qui doit être appliquée soit qu’on parle d’espace discret, soit qu’on parle d’espace continu.

6. Deux exemples

Je vais introduire maintenant deux exemples de diagrammes constructifs, c’est-à-dire de diagrammes qui contiennent un message sur la prochaine étape susceptible d’être réalisée sur eux-mêmes. Dans le premier cas constitué par la Fig.7, l’instruction porte sur la manière dont le sujet peut ajouter la rangée successive de points blancs discrets.

Fig.7

La tache est de montrer que la somme des premiers nombres impairs 2n-1 est équivalente à n au carré. En langage formel,

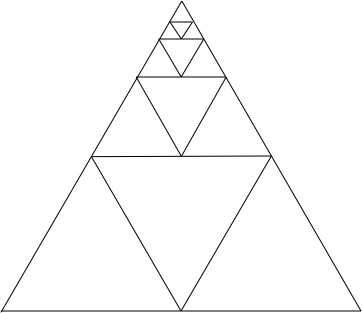
Dans le deuxième cas, en Fig.8, l’instruction donnée par le diagramme porte sur la manière dont le sujet peut prolonger les lignes continues du triangle plus grand pour qu’il puisse contenir d’autres triangles plus petits.

Fig.8

La tâche à réaliser consiste à montrer que la somme des puissances successives d’un quart est équivalente à un tiers. En langage formel, cela donne :

Ces deux diagrammes figurent sur les couvertures des deux livres de Nelsen publiés en 1997 et 2001, intitulés « Démonstrations sans paroles » (le titre original est Proofs without Words) (Nelsen, 1997, 2001). Le titre de ces livres est à vrai dire ambigu. En fait, il y a une ambiguïté dans le fait de considérer ces démonstrations comme « sans paroles », et j’espère que cette ambiguïté apparaît clairement, parvenus à ce point de mon argumentation. Ces démonstrations, en effet, ne sont pas sans paroles si en disant « sans paroles », on considère qu’il n’y a aucune interaction avec le langage. Par contre, ces diagrammes sont prévus pour la tâche consistant à démontrer un théorème et ce théorème est normalement exprimé au moyen d’une formule du langage mathématique. Il vaudrait mieux dire que ces diagrammes sont sans paroles pour la raison qu’ils présentent les instructions sur la manière dont le sujet doit les utiliser, mais ils ne décrivent pas en paroles ces instructions.

Je veux prendre en considération une objection potentielle relative au choix de mes deux exemples. En effet, j’ai privilégié la partie supérieure de l’axe vertical de ma classification, et je me suis concentrée sur l’aspect « constructif » de ces diagrammes. Quelqu’un pourrait me faire remarquer que ces exemples sont plutôt difficiles à placer sur l’axe horizontal : quelle est, dans ces cas, la correspondance entre la structure des diagrammes et la structure des données représentée ? En effet, je dois admettre que cette manœuvre est risquée, parce qu’elle va nous ramener à des considérations relatives à la nature de la réalité mathématique ou de la géométrie, mais je ne souhaite pas ici aborder ces questions. Je suis donc d’accord que ce serait une bonne chose de trouver des exemples de diagrammes constructifs moins ambigus par rapport à la place qu’il faut leur attribuer dans la classification.

7. Recherches envisagées et conclusions

L’esquisse de classification que je viens de présenter soulève plusieurs questions. Premièrement, on peut se demander s’il est possible de considérer un diagramme constructif séparément du système de représentation auquel il appartient. Et si on ne peut pas, comment peut-on définir un système de représentation ? Une deuxième question concerne la forme d’apprentissage qui est mise en jeu dans chacun de ces types de représentations externes. Une hypothèse est qu’il y a des représentations qui peuvent être utilisées, c’est-à-dire correctement manipulées, d’une façon qui exige un apprentissage plus rapide, et d’autres qui, en revanche, doivent être apprises plus attentivement. De surcroît, il faudrait développer la relation entre la capacité que les diagrammes possèdent de traiter l’information et de permettre aux sujets qui les utilisent de produire de nouvelles inférences, et le fait qu’ils sont caractérisés par leur espace physique ; en plus, il faudrait discuter si les diagrammes sont compris seulement quand le sujet est capable de les modifier : existe-il par exemple des manipulations qui s’appliquent « typiquement » à certains diagrammes particuliers ?

Pour ce que je peux en voir à ce stade de ma réflexion, il y a ici deux lignes de recherche envisageables. La première ligne de recherche va considérer le raisonnement spontané qui s’appuie sur les diagrammes. Le but sera de déterminer les contraintes que les sujets appliquent spontanément à certains types de diagrammes particuliers. Un domaine intéressant de ce point de vue est une étude sur le développement de la compréhension des diagrammes par des enfants d’âges différents. Bien sûr, il y aura des différences qui vont déterminer les avantages et désavantages du choix d’une méthode d'enseignement qui puisse améliorer les résultats. La deuxième ligne de recherche peut prendre la forme d’une étude de terrain relative aux activités de scientifiques de différentes disciplines. La question est de comprendre comment les diagrammes peuvent contribuer à la découverte ou à l’explication. D’autres articles du présent volume sont consacrés à ce point, en analysant des études de cas.

J’arrive maintenant à mes conclusions. La classification que j’ai proposée va au delà de la dichotomie visuel/linguistique, très présente dans la littérature traditionnelle, et cela, je crois, représente une étape nécessaire pour rendre compte de la complexité de l’utilisation des diagrammes. Sur la base de ma classification, j’ai souligné l'intérêt de considérer les diagrammes que j’ai défini à l’aide de l’adjectif « constructifs ». Ces diagrammes ne montrent pas seulement leurs contraintes visuelles et leurs contraintes interprétatives/symboliques, mais ils fournissent également des instructions par rapport aux manières dont ils doivent être manipulés. Cette esquisse de classification demande une étude approfondie des variables en jeu ainsi que la considération en profondeur d’études de cas différentes, et surtout appropriées.