La pensée graphique. Pour une sémiotique des diagrammes
N’efface pas mes circonférences.
Archimède dans Capek, La mort d’Archimède (1938)
1. Qu’est-ce qu’un diagramme ?
- Note de bas de page 1 :
-
Dans ces tentatives, à savoir le projet des « graphes existentiels » (Collected Papers, Vol. 4, Livre II), Peirce essaie de créer une écriture en deux dimensions spécifiquement destinée à montrer visuellement la structure des processus logiques du raisonnement. Il se lance ainsi dans une modélisation symbolique ou semi-symbolique fondée sur ses propres conventions grapho-sémantiques explicites, et non dans une étude des faits diagrammatiques existants. Le grand livre de F. Stjernfelt, Diagrammatology (2007), se tient, malgré son envergure philosophique et ses ambitions théoriques, trop près de Peirce pour aborder ce champ d’étude empirique que constitue le diagramme tel qu’il se pratique à l’état « sauvage » ; pour Stjernfelt, comme pour tant d’autres sémioticiens qui l’effleurent en passant, le diagramme constitue un cas d’iconicité non-problématique, et donc considéré en soi comme plutôt trivial, quoique occasionnellement illustratif en logique ou en modélisation.
Un diagramme est un fait graphique qui normalement apparaît dans un contexte verbal et qui est typiquement destiné à représenter le fonctionnement ou l’articulation d’un phénomène d’une certaine complexité causale. Ce contexte peut être un discours technique, théorique, analytique ou autre ; il s’agit régulièrement d’un discours épistémique, car la représentation diagrammatique représente un sens sous-jacent, un fonctionnement structurel, causal, etc. du phénomène en question plutôt que son apparence. « Image du sens », le diagramme n’est ni une constellation de symboles opérationnels arbitraires et conventionnels, comme le serait une équation, ni une composition iconique se référant à une perception possible, comme une photographie. Il est curieusement passé presque inaperçu dans la littérature sémiologique, qui, pourtant, s’en sert abondamment dans ses propres « illustrations » graphiques, et il n’a en effet jamais été abordé directement dans sa spécificité sémiotique, malgré les fameux diagrammes logiques d’un C. S. Peirce1.
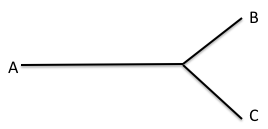
Pour montrer combien le diagramme problématise la sémiotique, prenons un simple diagramme de bifurcation (Fig. 1). Ce graphe peut se référer à un flux hypothétique A qui est censé se diviser en deux branches B et C, ou à une alternative conceptuelle, ou encore à l’idée d’un tout contenant deux parties, ou à bien d’autres choses encore. Mettons que, dans un contexte donné, il représente une proposition A qui se verra attribuer la valeur de Vraie (B) ou de Fausse (C).
Fig. 1. Graphe de bifurcation
J’imagine dans ce dernier cas la proposition comme une entité immatérielle parcourant la ligne A (dans le temps mental d’un acte de jugement épistémique) jusqu’à devoir assumer la valeur de vérité assignée à la branche B ou bien celle assignée à C : v(A) ou f(A). Puisque la forme bifurquante est motivée, elle n’est pas symbolique, au sens d’un signe conventionnel (comme ce serait le cas si la forme était celle d’un signe de l’écriture assyrienne semblable, par exemple – tel que waw). Et dans la mesure où elle ne représente rien de sensible qui pourrait fonder une similarité, il n’est pas possible de la déclarer iconique. Ce que représente cette forme – dans le contexte et avec l’apposition (celle-là conventionnelle) des symboles A, B et C – est une « imagination » par laquelle une entité propositionnelle se voit attribuer tel prédicat épistémique, véridictoire. Cette « imagination », cette chose eidétique, est présente à mon esprit au moment où je me sers de ce diagramme pour extérioriser une partie de ce que me donne à voir ma vision intérieure, qui s’exprime mentalement ainsi. Comment appeler cette vision mixte, extérieure-intérieure ?
- Note de bas de page 2 :
-
Le diagramme serait ainsi lié directement à ce que le philosophe J. Fodor appelle « le langage de la pensée », cf. : J. Fodor, LOT 2 : The Language of Thought Revisited (2008). S’agit-il pourtant d’un « langage », voire d’une « langue » ? La question de savoir dans quelle mesure cette activité graphique mentale est systématique, reste ouverte.
La question de savoir quel statut sémiotique attribuer à ce diagramme n’est pas triviale. Si une alternative peut spontanément se représenter par une bifurcation, sans présupposer un codage conventionnel, c’est que la bifurcation s’y prête déjà, c’est un schéma naturel de l’alternative. Le diagramme, à l’instar de beaucoup de gestes « figuratifs » spontanés, qui fonctionnent sans codage conventionnel, semble bien montrer graphiquement comment nous schématisons, au moment même de penser ou de communiquer ce que nous pensons et essayons de dire. Le sens du diagramme consiste pour ainsi dire en un graphe mental identique – du moins partiellement – au graphe qu’il nous arrive de dessiner ou d’esquisser gestuellement. On pourrait dire par conséquent que le diagramme est un indice du mécanisme cognitif, qui schématise graphiquement au cours de l’élaboration d’une pensée2. Nous allons retenir et développer cette hypothèse du double statut du diagramme, sémiotique et cognitif, dans ce qui suit.
2. Quels sont les graphes d’un diagramme ?
En sémantique cognitive, les schémas dynamiques, cinétiques ou statiques dont se servent les linguistes (R. Langacker, L. Talmy, G. Fauconnier et alii, passim) sont régulièrement représentés par des diagrammes. Chaque chercheur a son style diagrammatique reconnaissable, signé. Ces diagrammes illustrent souvent certaines propriétés sémantiques relationnelles des morphologies, par exemples des prépositions, des conjonctions, des adverbes satellites (up, down, in out, off…). C’est que la morphologie est sémantiquement distincte du vocabulaire en général, elle schématise, alors que la lexicologie catégorise. La différence entre les catégories et les schémas, dans une langue, c’est précisément que ces derniers s’expriment par des morphèmes (relevant des « classes fermées », en termes de parties du discours), alors que les premiers s’expriment par des prototypes nominaux ou verbaux (relevant des « classes ouvertes »). La mise en relation eidétique des catégories, au cours de la construction d’une pensée, se fait par les schémas ; corrélativement, dans les diagrammes, les graphes mettent en relation le contenu catégoriel, représenté par les indications symboliques apposées au diagramme. Comme nous venons de le voir, les parties notables d’un diagramme appellent des symboles (A, B, C), qui, à leur tour, renvoient à des catégories ou à des propriétés catégorielles. Une pensée stéréotypique consisterait ainsi en une construction schématico-catégorielle figée et immuable. Une activité cognitive fluide et variable, en revanche, recompose sans cesse les constellations schématico-catégorielles, en les recatégorisant ou en les reschématisant ; c’est essentiellement ce en quoi consiste la « réflexion ». La distinction entre catégories et schémas est donc d’une importance capitale, à la fois cognitive et sémiotique, pour l’étude du sens.
- Note de bas de page 3 :
-
Fermé / ouvert au sens des classes ouvertes ou fermées du vocabulaire d’une langue.
En étudiant les manifestations diagrammatiques sur les tableaux noirs (ou blancs) des salles de cours académiques, dans les textes scientifiques et pédagogiques, les modes d’emploi techniques, etc., sans oublier les griffonnages improvisés des chercheurs, il est possible de se former une impression d’ensemble sur l’inventaire éventuel des figures apparaissant dans ces expressions. L’intuition nous dit que cet inventaire constituera un ensemble ouvert, formant une liste infinie de types de graphes de toute sorte ; mais, d’autre part, il n’est pas exclu que cet ensemble s’avère fermé3. Dans ce qui suit, nous allons proposer, à titre heuristique, une liste très réduite, quoique non nécessairement exhaustive, d’un tel inventaire, une liste courte qui, fermée ou non, nous permet déjà d’envisager une combinatoire « grammaticale » du diagramme. Nous distinguerons ici les « diagrammèmes » suivants : les flux, les flèches, les fermés, les liens, les lignes de partage, et finalement les contours, avec leur métrique.
2.1. Les FLUX. Ce sont des lignes orientées qui montrent les parcours possibles dans un réseau, avec ses confluences, ses bifurcations et ses bassins et turbulences éventuels.
2.1a. En voici un exemple simple :
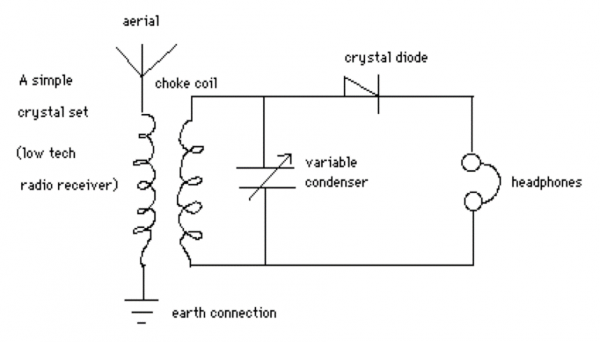
Fig. 2. Diagramme d’un poste à galène, trouvé sur un tableau de classe en physique
- Note de bas de page 4 :
-
Un « icône » en ce sens est effectivement une image visuelle de l’objet visé, mais simplifiée jusqu’à se réduire à un graphème désignant la catégorie de l’objet, et non pas un exemplaire singulier.
Le plan de construction d’un poste primitif de radio, dessiné à la main. Les flux électriques provoqués par les ondes captées par l’antenne font passer le courant dans les deux sens, ce pourquoi la diode, qui le redresse, est nécessaire. Le condensateur variable, mis en parallèle avec la bobine, permet de sélectionner la fréquence d’ondes ; on n’a pas besoin d’amplification avec un casque radiophonique classique pour pouvoir écouter les chaînes en ondes courtes et moyennes. C’est l’appareil le plus simple et le plus écologique possible. Ses composantes (antenne, bobine double, diode, condensateur, casque, etc.) sont représentées par des « icônes » symboliques4 :
2.1b. Les schémas dynamiques en forces-et-barrières que les linguistes utilisent pour rendre compte du sens des verbes modaux, par exemple pouvoir vs devoir, sont représentés par des diagrammes de flux à entraves tels que celui-ci.
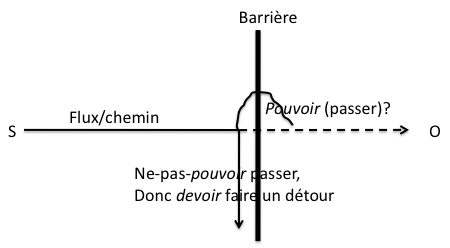
Fig. 3. Schéma dynamique du sens modal des verbes pouvoir vs. devoir (faire)
Évidemment, il faut imaginer une entité mobile (S, sujet) suivant le flux indiqué pour surmonter la barrière avant de joindre son objet (O) ; cependant, S et O ne sont que des êtres symboliques, pour ainsi dire pronominaux, et seul l’aspect dynamique du rapport S–O est représenté par ce diagramme. Le sens des verbes modaux est purement schématique, et le sens schématique peut migrer d’un domaine expérientiel à l’autre : la conjoncture modale peut alors devenir épistémique (pouvoir-penser), déontique (pouvoir-se-permettre-de-faire), physique (être-capable-de-faire), ou symbolique (pouvoir-déclarer), alors que le schéma lui-même reste neutre face à ces variations sémantiques. On utilise les mêmes schémas dans tous les domaines, mais non les mêmes catégories ; par conséquent, le même style de logique “spontanée” peut s’appliquer à tout le pensable, et la même morphologie grammaticale s’applique à tous les thèmes dont il est possible de parler, quels que soient le domaine sémantique et sa spécificité terminologique.
- Note de bas de page 5 :
-
On trouve un schéma dynamique dans E. Sweetser, From Etymology to Pragmatics, 1990, dans une description de la sémantique modale. Elle renvoie au pionnier Leonard Talmy, qui avait proposé d’autres variantes de ces force-dynamic schemas dès les années 1970 ; voir L. Talmy, Toward a Cognitive Semantics (2000).
Dans ce schéma5, une entité S parcourt le chemin direct vers O, son « but », (car nous sommes dans la causalité intentionnelle) avant d’être arrêtée par une barrière qui l’oblige à dévier, si elle n’arrive pas à la surmonter. La barrière est ou bien un second flux qui bloque le premier, ou bien un autre diagrammème : un répulseur (relevant du soi-disant “container” » ; il s’agit du « mur » qui entoure le fermé, le chorème, voir ci-dessous). Le diagramme dynamique des modalités – qui peut bien entendu se nuancer selon la sémantique modale des langues, des constructions grammaticales, ou des textes – semble relever originairement d’une pensée intentionnellement causale : on doit faire X, si on veut atteindre O ; on peut devoir faire X sans pouvoir faire X, etc.
Une conséquence particulièrement intéressante du rôle des flux dans la diagrammatique de notre pensée est que les bifurcations peuvent ainsi « s’influer » en s’entrecoupant. C’est ce qui nous permet de lier des idées voisines par la relation dite d’implication et, en général, par des liens conditionnels, comme dans l’exemple suivant.
2.1c. La branche d’une bifurcation peut devenir la barrière coupant et bloquant l’une des branches d’une autre bifurcation, ce qui provoque un changement dynamique de ce second flux.
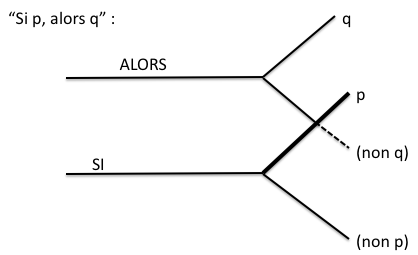
Fig. 4. L’implication
La circonstance p implique q. Pour lire ce diagramme, il faut évidemment supposer une entité X susceptible de devenir porteuse de la propriété p et une entité Y qui pourra assumer la propriété q. Si la conjoncture p de X arrive à bloquer la conjoncture non-q de Y, alors on aura q « à cause de » p. La circonstance p de X provoque la circonstance q de Y. La même conjonction /si/ (en angl. /if/) peut d’ailleurs introduire une subordonnée interrogative – « je ne sais pas si tu es d’accord (ou non) » – , précisément parce qu’elle porte en elle la bifurcation, dans la construction interrogative comme dans la conditionnelle. Nous laissons au lecteur curieux de deviner ce que serait le schéma de l’exception à une telle régularité conditionnelle. La protase (si p de X) de la formule conditionnelle est donnée dans la modalité du /possible/ ; p et non-p sont les possibles alternatifs ; l’apodose (q de Y) subit un changement de sa valeur modale, qui de /possible/ devient /nécessaire/, quand non-q est devenu impossible, puisque bloqué par p. Voici la figure sans doute la plus importante de toute pensée. Il peut évidemment s’agir de deux personnes, X et Y, dont l’une modifie la « liberté » de l’autre par une obligation ; le rapport interpersonnel est essentiellement modal, ce qui se manifeste dans toute négociation.
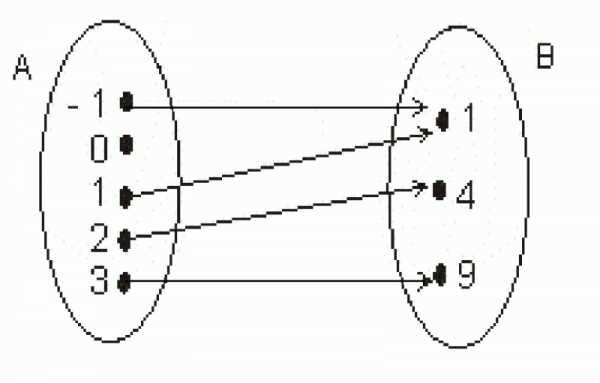
2.2. Les FLÈCHES. Ce sont des indicateurs spatio-temporels ou déictiques. Elles orientent notre attention, ou bien d’une chose vers une autre, qui suivrait ou correspondrait à la première, pour quelque raison, typiquement parce que la dernière est le résultat d’une transformation régulière de la première ; ou bien elles appellent simplement notre attention directement vers une chose, déictiquement.
Fig. 5. Valeurs quadratiques
- Note de bas de page 6 :
-
Les flux sont continuistes, les flèches discontinuistes, pourrait-on dire.
Les projections, “mappings”, ou correspondances, entre deux collections d’objets, c’est-à-dire les opérations de toutes sortes qui établissent de telles relations avec une certaine régularité, typiquement entre deux cadres, ensembles, situations, lieux ou espaces conceptuels, sont universellement représentées par ces flèches. On varie sur leur épaisseur, leur longueur, la consistance pleine ou pointillée de leur corps pour indiquer leur importance relative ou leur statut épistémique. Les flèches apparaissent souvent en faisceaux, comme dans cet exemple, pour signifier des transformations corrélatives. Il s’agit souvent, encore comme dans l’exemple ci-dessus, de la mise en relation de deux domaines d’ordre différent et séparés d’un vacuum spatial représentant la ratio de la corrélation – cela d’ailleurs par contraste avec les flux6, qui relient les lieux, alors que les flèches les séparent.
- Note de bas de page 7 :
-
La chorématique, étude de la logique des lieux, introduite dans un ouvrage de 1982 en danois, fait aussi l’objet d’un chapitre, « La sémiotique de l’être », de notre thèse d’Etat, La Charpente modale du sens. Pour une sémio-linguistique morphogénétique et dynamique, publiée en 1992, Ed. John Benjamins et Aarhus University Press. Le chorème est une notion plus développée que celle de « container » à beaucoup d’égards. Il sert à schématiser un très grand nombre de phénomènes morphologiques verbaux et périphrastiques, alors que le « container schema » est notamment mis en œuvre pour rendre compte de la simple différence entre /in/ et /out/, ou /dedans/ vs /dehors/.
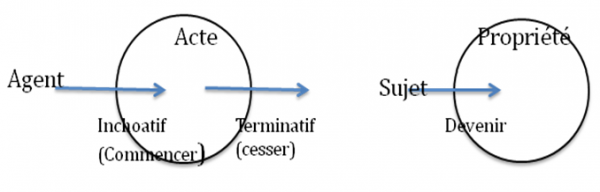
2.3. Les FERMÉS. Ces entités (en anglais : “container schemas” ; en sémiotique : chorèmes7) séparent un intérieur et un extérieur et permettent ainsi à un essaim d’objets intégrés ou à une masse de former un tout qualifié, à l’exclusion des objets ou des parties de la masse qui ne se « qualifient » pas pour en « faire partie ». Un fermé est protégé de l’extérieur par une barrière circulaire (fermée) résistante aux flux venant de l’extérieur ou de l’intérieur. Entrer et sortir sont donc les événements les plus remarquables caractérisant ces entités totalitaires de qualification. Les actes et les propriétés sont typiquement représentés par des fermés. (Ainsi, on peut « entrer en fonction » : l’agent entre dans le chorème fermé de la fonction, conçue comme un lieu conceptuel). Les fermés divisent l’espace en deux zones, la zone marquée, interne, et la non-marquée, externe, d’où partent les entités mobiles dont on décrit, c’est-à-dire imagine, les statuts changeants. Ils peuvent s’enchâsser et s’entrecouper, ce qui donne lieu aux fameux cercles d’Euler. Ils peuvent représenter des lieux conceptuels ou sociaux, des états ou des actes, et permettent de les penser comme dotés d’une « entrée » et d’une « sortie » (cf. « être en colère », « cesser de s’inquiéter », « commencer à travailler », etc.). Le sens aspectuel renvoie à des parcours d’agent sur le chorème de l’action ; le devenir renvoie à la version non-agentive, nominale, qui décrit la traversée du chorème d’une propriété par un sujet. En voici deux exemples simples.
Fig. 6. Aspectualités verbale et nominale
Comme il arrive souvent, la morphologie schématique est plus développée dans le domaine verbal (de l’acte ou de l’événement) que dans le domaine nominal (de l’état et de la prédication).
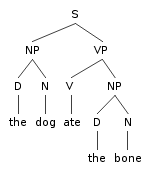
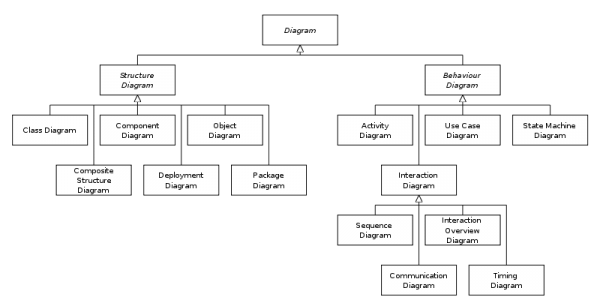
2.4. Les LIENS expriment des rapports de dépendance, des hiérarchies. Une chose est subordonnée à une autre par un lien, typiquement représenté comme une corde de suspension verticale ou de spécification horizontale. En général, cette subordination constitue une dépendance de plusieurs entités par rapport aux entités qui les contrôlent, et qui les tiennent comme en laisse par des « nœuds » (nodes). Les arbres phrastiques, les hiérarchies catégoriales et les structures sociales de tous ordres sont souvent représentés ainsi.
Fig. 7. Deux arbres de dépendances, l’une structurelle, l’autre classificatoire
La représentativité politique dans les systèmes démocratiques est un exemple éminent : les éléments subordonnés s’y trouvent « représentés » par des éléments supérieurs qui parlent à leur place en s’adressant à un élément encore supérieur au représentant, et ainsi de suite. « Parler au nom de quelqu’un » est une notion relevant de ce schéma. L’instance supérieure se substitue à l’inférieure. Dans la philosophie sémiotique de Peirce, où aliquid stat pro aliquo (something stands for something else), on aurait une hiérarchie représentative infinie dans les deux sens de la verticalité substitutive, sans base ni fin, sans plancher ni plafond : le monde.
2.5. Les LIGNES DE PARTAGE. Ce sont, de manière élémentaire, les lignes que nous traçons pour marquer une limite, une frontière, une différence. « D’un côté X, de l’autre, Y », comme nous disons en faisant le geste manuel d’un marquage de ligne verticale dans l’espace devant nous. La ligne de partage n’est pas franchie, car ce n’est pas une barrière, elle marque purement et simplement une distinction de strate sémantique – entre deux points de vue politiques, entre deux sens d’un terme, entre deux principes juridiques, etc. C’est une coupure, faite par un instrument imaginaire, un couteau mental, pour ainsi dire. La propriété se diagrammatise ainsi : voici ce qui est à moi et ce qui est à toi. Si l’espace soumis à cette division est déjà fermé, nous avons en effet le cas bien connu du « camembert » de partition d’une totalité.
Fig. 8. Le camembert méréologique
Rien dans le monde des données visuelles ne ressemble à un tel camembert (sauf évidemment un camembert), et pourtant ce graphe offre une vision fort utile des proportions respectives des portions quantitatives d’un tout prédéfini. Bien entendu, ce tout se referme sans parties vides si l’on enlève telle portion spécifiée ; c’est là la logique du « gâteau » méréologique, comme d’un budget fixe. Un tout est toujours total ! Dans l’exemple ci-dessus, le tout serait toujours 100 %, même si les ventes du premier quadrimestre étaient nulles (zéro). Le camembert est plastique. Méréologiquement, ce diagramme nous permet de penser la composition d’un ensemble sans rien envisager d’autre que le poids respectif des parties (en oubliant par exemple la structure locale et partielle qui les organiserait).
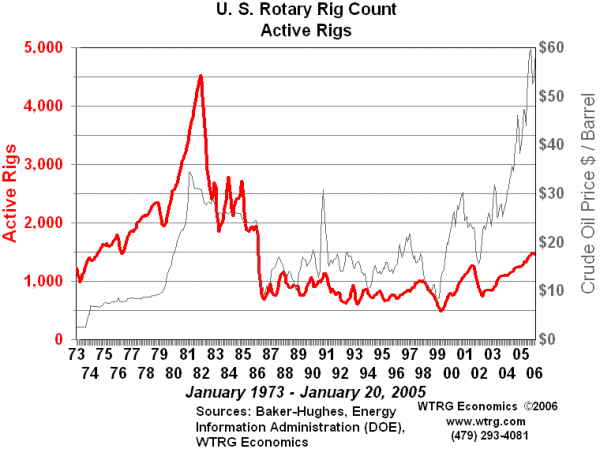
2.6. Les CONTOURS. Quand nous voulons comparer des quantités et, par exemple, considérer la montée ou la descente des impôts, des prix, ou de n’importe quelle autre valeur variable, dont la « hauteur » varie, par exemple, dans le temps, nous voyons mentalement un contour comme celui d’une chose ou d’une masse scannée dans l’espace. Un tel contour présuppose toujours une métrique, c’est-à-dire son inscription dans un cadre topologique mesurable, permettant d’interpréter les valeurs en « hauteur » en fonction des variables en « largeur » et éventuellement en « profondeur ». Cette condition métrique ne s’impose pas aux autres graphes ou diagrammèmes, mais peut facilement être introduite, pour les besoins de comparaisons quantitatives. L’exemple suivant montre les contours à la fois du nombre des lieux de forage et du prix par tonneau de pétrole, et permet donc de contempler leurs covariations pendant une période (de 32 ans). La constellation des trois axes métriques – nombre de tours, montant du prix, et temps – permet d’étudier les régularités éventuelles de leurs covariations, qui peuvent aller de la fonction mathématique simple jusqu’au chaos, manifestant le plus souvent un compromis entre ces extrêmes.
Fig. 9. Tours de forage et prix du pétrole
- Note de bas de page 8 :
-
Fauconnier & Turner (The Way We Think, 2002) appellent ce phénomène une « compression » conceptuelle : ainsi, le dinosaure devient un oiseau, comme si cela se faisait au cours d’une seule génération dans l’évolution animale.
Les contours sont toujours les signifiants quantitatifs de nos idées comparatives : la longueur des jupes et l’envergure de la créativité humaine varient, comme on sait, selon la conjoncture économique du monde… Le cadre métrique du diagramme dit cartésien, composé de deux axes métriques, est bien entendu une invention moderne, destinée à développer une géométrie analytique ; mais l’intuition fonctionnelle sous-jacente, celle d’une covariation possible, est certainement archaïque (« La limousine du général devient plus longue chaque année… » ; « Lorsqu’on va vers le nord, les palmiers disparaissent… », etc.). On peut proposer de dire que le contour lui-même, variation quantitative sur une multitude de faits, devient un seul fait graphique – les prix devenant le prix, etc. – par une opération8 qui assimile les mouvements du contour à ceux d’un animal minuscule errant, bousculé par son environnement, ou plutôt à son trajet incertain et fluctuant, exposé aux conditions extérieures changeantes.
Les diagrammes de notre vie cognitive de tous les jours sont souvent des combinaisons de ces six types graphiques, et il est à la limite possible que cette combinatoire rende compte de l’essentiel des représentations diagrammatiques ; ainsi nos opérations mentales de schématisation, apparemment infiniment complexes disposeraient, pour se dérouler rapidement et de manière fluide, d’une grammaire élémentaire, d’une sémiotique structurée. Quoi qu’il en soit, pour comprendre la problématique diagrammatique de manière plus profonde, il faut aborder une question moins souvent discutée, mais aussi importante : celle de la complexité de l’espace même du diagramme.
3. La spatialité diagrammatique
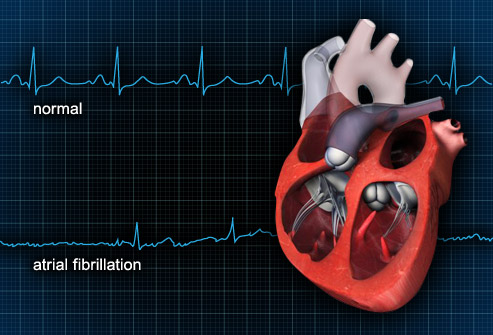
Considérons un diagramme pratique, soit une représentation neuronale bien-connue comme la suivante, prise dans une présentation des maladies cardiaques :
Fig. 10. Rythmes du cœur
- Note de bas de page 9 :
-
On peut éventuellement dire qu’ainsi les trois ordres du signe peircéen se retrouvent, l’iconique, le symbolique, et l’indiciel – dans la mesure où l’indice serait représenté par le diagramme métrique comme manifestation de l’eidétique même. Les trois ordres se superposeraient typiquement dans la spatialité stratifiée du diagramme investi. Il faudrait donc désormais distinguer entre le diagramme pur, eidétique, et le diagramme tri-spatial, sémiotiquement investi, contextualisé.
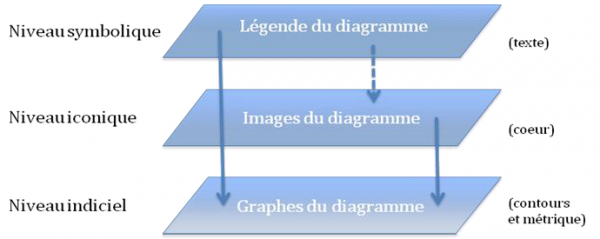
Il est évident que le cœur sectionné représenté ici n’est pas supposé être traversé par les contours des pulsations, soit normales, soit devenues anormales par fibrillation, comme s’ils étaient des fils de fer, mais que, bien entendu, l’espace de ces contours, sur un fond quadrillé, constitue un plan spatial différent de celui où se trouverait le cœur iconiquement esquissé. L’espace diagrammatique proprement dit est donc ici donné comme sous-jacent à l’espace iconique, puisque nous voyons le cœur se poser sur le contour. Ce cœur repose donc pour ainsi dire sur une surface diagrammatique quadrillée, métrique. De plus, la légende – normal / atrial fibrillation – quoique relevant de l’écriture langagière, n’appartient pas non plus à la surface diagrammatique, mais s’y superpose comme une explication, une légende, sans pour autant rejoindre le niveau spatial du cœur, puisque les lettres et le cœur n’habitent pas un même espace. Nous voilà ainsi en présence d’une constellation de trois espaces, le premier iconique (celui du cœur), le second diagrammatique (celui des contours), et le dernier symbolique (celui de la légende)9. On aura une architecture telle que celle-ci :
Fig. 11. Stratification spatiale du diagramme investi
Ce diagramme du diagramme – que nous proposons pour rendre compte du phénomène tri-spatial –manifeste d’ailleurs une fonction typique des flèches : la projection d’un ensemble à un autre, à travers le vide.
- Note de bas de page 10 :
-
La peinture monochrome constitue un cas limite de criticité maximale et minimale à la fois, selon le point de vue : maximale pour une lecture symbolique, minimale, voire nulle, pour une lecture iconique. Dans celle-là, le sens global serait une sorte d’injonction à la méditation; dans celle-ci, une invitation à admirer le jeu infini des nuances lumineuses locales dans une surface monochrome mais non mono-photonique.
3.1. Densité spatiale. Pour voir qu’il s’agit d’espaces distincts, on peut considérer ce qu’il convient d’appeler la densité spatiale respective. Dans chaque espace, un fonctionnement sémiotique est donc à l’œuvre et il repose sur une covariation du signifiant et du signifié. Une variation dans le plan du signifiant, conçue comme un passage minimal entre deux points dans ce plan, produit ou ne produit pas une variation dans le plan du signifié, c’est-à-dire un changement de sens. Si la variation du signifiant est productive en ce sens, c’est qu’elle a lieu à un endroit critique dans l’espace signifiant ; dans un espace symbolique, par exemple la page d’un texte écrit, les “lignes” de l’écriture, les traits des lettres, les blancs et la ponctuation constituent des zones critiques, tandis que les marges et l’espace vide entre ces “lignes” restent non critiques. Les espaces symboliques sont les moins riches en zones critiques de l’ensemble des espaces signifiants possibles ; leur densité signifiante est donc minimale. Cela caractérise et distingue leur fonction sémiotique. En revanche, les espaces iconiques contiennent des zones beaucoup plus étendues de “criticité”, à savoir celles qui offrent des représentations figuratives, typiquement au premier plan ; l’arrière-fond, en revanche, est souvent flou, diffus et, à la limite, insignifiant. Les espaces iconiques sont les plus denses de toutes les fonctions sémiotiques, sans que, pourtant, cette densité maximale n’atteigne jamais une hypothétique saturation totale du cadre spatial10 – ce qui correspondrait à une forme d’attention perceptive à focalisation globale… Or, les espaces diagrammatiques se trouvent dans une position médiane dans l’échelle de densité. Leurs composantes graphiques – traits, plaques chromatiques, etc. – forment bien sûr des zones critiques, mais elles se trouvent entourées de grandes zones vides. Les espaces diagrammatiques n’ont pas de “lignes” d’écriture, et les deux dimensions du support visuel (matérialisé ou gestuellement marqué) sont toujours exploitées, dans une certaine mesure : la verticalité indiquant des dépendances, et l’horizontalité des oppositions, par exemple. Pourtant, la profondeur de la perspective iconique est absente, à moins qu’il ne s’agisse d’une composante localement iconique (un cube pour signifier une “boîte noire”, par exemple).
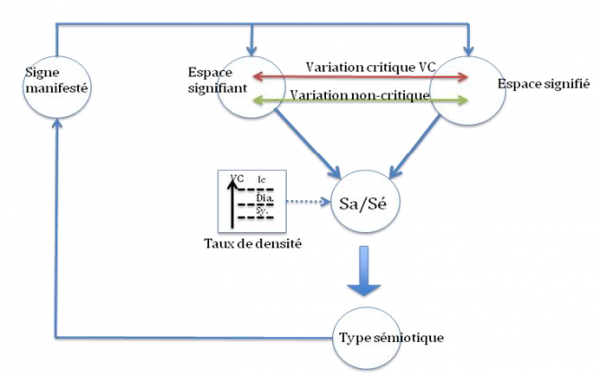
Ce que nous venons de proposer sur la densité spatiale du signifiant peut se résumer en un réseau d’espaces mentaux tel que celui-ci :
Fig. 12. Relations critiques et densité de l’espace signifiant
- Note de bas de page 11 :
-
Le format de ce réseau d’espaces mentaux suit celui présenté dans notre livre, Spaces, Domains, and Meaning (Peter Lang, Série Sémiotique Européenne, Vol. 4, 2004) et dans L. Brandt & P. Aa. Brandt, « Making Sense of a Blend. A Cognitive-semiotic Approach to Metaphor », in Annual Review of Cognitive Linguistics, 3, 2005.
Ce réseau11 décrit l’analyse mentale que nous effectuons en séparant les espaces du signifiant et du signifié pour ensuite considérer, dans le cas d’une manifestation sémiotique donnée, la structure critique de cet objet signifiant, sa densité sémiotique, et partant le type sémiotique de cette manifestation.
3.2 Densité et force modale. L’intérêt de déterminer le type d’une fonction sémiotique concerne par ailleurs sa valeur modale, car la force modale est inversement proportionnelle à la densité. Comme l’avait vu C. S. Peirce, l’icône est un « signe de possibilité », c’est-à-dire que l’image de quelque chose n’indique que la pure et simple possibilité, et non la nécessité, de la configuration de propriétés montrée ; en revanche, le symbole est toujours une instruction, indiquant quelque forme de devoir-faire, donc de nécessité, tels une équation, un feu de circulation, un signe d’interdiction de fumer, une croix ou un élément vestimentaire signifiant la dévotion religieuse du porteur et l’obligation déontique de respect revendiqué.
Dans un diagramme investi, avec ses trois espaces en superposition, tel que celui de la figure 10, supra, nous aurons donc à parcourir trois fois le réseau (fig. 12), et nous aurons, corrélativement, trois couches de sens modal. Voici le cœur, qui peut se présenter ainsi dans des circonstances particulières ; voici son battement en deux versions probables ; voilà ce qui est normal (comme il doit être) et ce qui ne l’est pas (comme il doit ne pas être), et voici le nom de cette anomalie : fibrillation atriale.
Les graphes font pour ainsi dire le pont entre les représentations symboliques et les représentations iconiques dans le diagramme ; on peut même penser cette transition comme un pontage cognitif : la pensée ne procède pas en combinant simplement des symboles (ils sont trop abstraits), et elle n’est pas entièrement iconique non plus (les images étant trop concrètes). Elle combine le symbolique et l’imaginaire iconique à travers le schématique, sémiotisé par les diagrammes, mentaux ou manifestés ; c’est donc cet élément, ce pont, qui nous permet à proprement dire de penser.
4. Conclusion
Les diagrammes échappent souvent à l’analyse des philosophes et des sémiologues, dans la mesure où ces formes d’expression (mentale ou matérielle) ne procèdent pas d’un système au sens d’un code conscient, explicite et représenté, mais relèvent d’une activité sémiotique spontanée plutôt pré-consciente et pré-réflexive. Il se peut que, dans la longue durée de l’évolution sémiotico-culturelle de notre espèce, les flux et les flèches, etc. aient migré du domaine des outils pertinents pour le travail et l’expérience quotidiens au domaine de l’activité mentale plus ou moins abstraite qui crée ce que nous appelons la réflexion. En effet, notre pensée s’applique aux choses passées et futures pour préparer nos actes qui doivent répondre aux défis physiques, sociaux, interpersonnels, ou même intra-psychiques et elle ne peut guère changer de « vocabulaire » mental pour chaque passage entre ces domaines, souvent d’importance égale dans les problèmes complexes de notre vie. De la même manière que le langage, qui conserve ses connecteurs morphologiques et les utilise à travers les domaines, la sémiotique de notre pensée conserverait et utiliserait les mêmes représentants graphico-mentaux, sans égard pour les domaines où un problème se pose à l’esprit.
Le phénomène universellement salué comme l’instigateur de l’historicité, au cours de notre évolution culturelle, l’écriture, peut être le résultat d’un glissement incertain à partir de certaines représentations denses, aboutissant aux chiffres, aux lettres, aux notes musicales et aux symboles computationnels, à travers un stade diagrammatique qui reste avec nous. La grammatologie classique, linguistique ou philosophico-critique, s’est posé la question de savoir comment l’écrit s’impose à l’oral (au lieu de s’y soumettre) ; c’est évidemment que cette représentation graphique très spécialisée fait partie d’un magma représentatif où la main, l’œil et l’esprit communiquent « grammatiquement » et s’envoient en réseau toutes sortes de formes susceptibles d’avoir un sens, que la voix et sa grammaire langagière s’en mêle ou non. On peut risquer la formule selon laquelle cette grammatique entre en concurrence et conflit avec la grammaire au cours de l’évolution sémiotique. L’écriture en serait un résultat, quoique toujours conflictuel (d’où la question permanente dans notre modernité : est-ce qu’on doit parler comme on écrit ou inversement ?), et les diagrammes en serait un autre : ce qui se « diagramme » peut toujours se dire de beaucoup de manières, exactement comme l’être qui selon Aristote est pollakos legomenon. Peut-être pour la même raison : ce qui se pense de l’être se donne à penser en diagrammes.