Image, imagination et mathématique chez Descartes et Leibniz
Une interprétation « classique »
L’argumentaire du colloque nous invitait à « réfléchir sur le fait que la mathématisation permet de rendre comparables différentes formes de collecte de données », à réfléchir sur la manière dont la mathématique peut homogénéiser les données observationnelles mais aussi, sans doute, à ce qui se joue dans le passage des phénomènes physiques à leur expression dans le langage mathématique. Le même texte affirmait que « le rapport entre visualisation (particularité) et mathématisation (généralité) est au centre du débat philosophique portant sur la relation entre intuition et logique et entre perception et généralité ». Voilà deux points pour lesquels nous sommes, très largement, les héritiers de l’âge classique, qui a inventé la mathématisation de la physique et jeté les bases de la logique formelle.
Mathématisation de la physique, en effet : Galilée affirme que le livre de la nature est écrit en langage mathématique, que ses caractères sont les triangles et les cercles, et qu’on ne peut rien y comprendre si on n’en apprend pas d’abord le langage. En un geste dont A. Koyré a souligné le caractère très platonicien, on ramènerait l’ensemble des données sensibles à leur essence, qui est idéale, mathématique. Les couleurs, les odeurs, les saveurs ne seraient que l’effet produit sur notre système sensoriel par les figures et les mouvements qui constituent les choses. Le morceau de cire, qui vient d’être tiré de la ruche, qui n’a pas encore perdu la douceur du miel, qui retient encore quelque chose de l’odeur des fleurs dont il a été recueilli, etc., ce morceau de cire devrait être reconduit à ce qu’il est essentiellement : une portion d’étendue. Le monde physique, sensible, ne pourrait être connu que si on le rapporte à des idéalités mathématiques, à des cas idéaux que nous n’observons jamais dans la nature. La parabole que décrit la boule qui quitte le plan incliné de Galilée n’est jamais parfaitement conforme à la parabole mathématique, mais c’est néanmoins la parabole mathématique qui constitue la vérité du phénomène physique. La physique classique, mathématique, se constituerait au moins partiellement contre nos perceptions, contre notre intuition immédiate (la physique d’Aristote y est bien davantage conforme).
- Note de bas de page 1 :
-
« Kant concevait […] les mathématiques comme les sciences du nombre et de la grandeur et même plus étroitement encore comme les sciences de l’espace et du temps, et non pas comme une science ou plutôt une méthode purement formelle, comme un ensemble de raisonnements déductifs et hypothétiquement nécessaires. Ici encore, on ne saurait lui reprocher de n’avoir pas prévu l’avenir, encore que, sur ce point aussi, Leibniz ait vu plus clair et plus loin que lui, et ait conçu fort nettement la mathématique universelle et plus spécialement l’algèbre universelle (qu’il appelait la caractéristique) comme applicable à toutes les formes possibles de déduction ». L. Couturat, Les principes mathématiques, Paris, Alcan, 1905. Cité par D. Rabouin, Mathesis universalis. L’idée de « mathématique universelle » d’Aristote à Descartes, PUF, 2009, p. 353.
D’autre part, au sein même des mathématiques, on assisterait à un mouvement d’éloignement par rapport à l’intuition visuelle. Grâce aux coordonnées qui portent son nom, Descartes parviendrait à passer des figures géométriques à leurs équations, à algébriser la géométrie et Leibniz ferait un pas de plus puisqu’il entrevoit la possibilité de ramener l’ensemble des mathématiques (et même l’ensemble du savoir) à un calcul formel, dont il s’efforcera d’ailleurs de jeter les bases. Cette interprétation logiciste de Leibniz a, on le sait, été notamment soutenue par B. Russel et L. Couturat (pour qui le schématisme kantien et le rôle central qu’il fait jouer à l’imagination ne serait, comme le dit David Rabouin, qu’une parenthèse malheureuse dans cette marche des mathématiques vers leur destin formaliste1).
- Note de bas de page 2 :
-
Voir, outre l’ouvrage cité dans la note précédente, l’article « Logique, mathématique et imagination dans la philosophie de Leibniz », Corpus, 49, 2005, pp. 165-198.
Double prise de distance, donc, de la science classique par rapport au monde de la perception, double mouvement d’éloignement par rapport aux images et à l’imagination : on ramène l’ensemble du monde sensible aux cercles et aux triangles puis on ramène les cercles et les triangles à leurs équations, à une expression formelle, objet de « la pensée aveugle », pour reprendre une expression de Leibniz. Cette interprétation est, on le notera, en parfaite consonance avec le thème cartésien – mais aussi pascalien, spinoziste, leibnizien ou malebranchiste – du caractère douteux des données des sens. Et avec les multiples mises en garde de ces auteurs contre l’imagination, « folle du logis », « maîtresse d’erreur et de fausseté ». La seule vraie connaissance serait celle de l’entendement pur, qui est parvenu à s’arracher aux illusions des sens, réalisant ainsi l’objectif des Méditations métaphysiques : Abducere mentem a sensibus, détacher l’esprit des sens. Pour le dire trop vite, le XVIIe siècle annoncerait le passage de l’intuition à la logique qu’auraient accompli les grandes théories formalistes de la fin du XIXe. C’est cette interprétation que je voudrais interroger, en mettant en partie mes pas dans ceux de Rabouin, qui explore depuis plusieurs années la question du rapport entre pensée et spatialité et qui, en particulier, s’est attaché à montrer l’importance de l’imagination mathématique à l’âge classique2. Pour le dire très vite c’est, selon Rabouin, par une sorte d’erreur rétrospective que l’on verrait aujourd’hui dans le développement des mathématiques cartésiennes et leibniziennes un progrès du formalisme contre l’intuition et l’imagination. Je voudrais expliciter cette thèse en la confrontant à quelques textes de Descartes puis en ajoutant rapidement quelques mots à propos de Leibniz.
Le projet des Regulae
- Note de bas de page 3 :
-
« Que si je veux penser à un chiliogone, je conçois bien à la vérité que c’est une figure composée de mille côtés, aussi facilement que je conçois qu'un triangle est une figure composée de trois côtés seulement ; mais je ne puis pas imaginer les mille côtés d’un chiliogone, comme je fais les trois d’un triangle, ni, pour ainsi dire, les regarder comme présents avec les yeux de mon esprit. Et quoique, suivant la coutume que j’ai de me servir toujours de mon imagination, lorsque je pense aux choses corporelles, il arrive qu'en concevant un chiliogone je me représente confusément quelque figure, toutefois il est très évident que cette figure n’est point un chiliogone, puisqu’elle ne diffère nullement de celle que je me représenterais, si je pensais à un myriagone, ou à quelque autre figure de beaucoup de côtés ; et qu’elle ne sert en aucune façon à découvrir les propriétés qui font la différence du chiliogone d’avec les autres polygones », Méditation sixième, édition Adam et Tannery (cité AT ci-dessous), IX, 57.
Le titre complet de cette œuvre de jeunesse de Descartes est, on le sait, Regulae ad directionem ingenii. Or l’ingenium dont il est question dans le titre n’est pas « l’entendement pur », mais l’entendement en tant qu’il est aidé par les autres facultés et, en particulier, par l’imagination. Descartes le dit tout à fait explicitement. L’idée que l’entendement perçoit mieux lorsqu’il est aidé par les sens ou l’imagination peut sembler étonnante. Il est en effet possible d’alléguer une multitude de textes dans lesquels Descartes affirme au contraire que les sens et l’imagination constituent des obstacles à la vraie connaissance, celle de l’entendement pur. Les Méditations reviennent sans cesse sur ce thème. Dans l’ordre métaphysique, bien sûr, mais peut-être aussi en mathématique. Par exemple, dans la Sixième Méditation, Descartes affirme que si nous pouvons concevoir un chiliogone aussi précisément qu’un triangle, nous ne pouvons en revanche l’imaginer que confusément. La preuve : notre imagination est incapable de distinguer le chiliogone, figure à mille côtés, du myriagone, figure à dix mille côtés3. Passage que l’on interprète volontiers, mais peut-être trop rapidement, comme une condamnation du recours à l’imagination en mathématique et l’affirmation d’une opposition entre entendement et imagination. Or, c’est très précisément de la collaboration, si je puis dire, qui doit s’instaurer entre entendement et imagination qu’il s’agit dans les Regulae. Ce texte me semble important pour notre propos parce que Descartes entreprend d’y développer un schématisme qui permet (ou devrait permettre) de rendre visible les opérations mathématiques et qui devrait même s’appliquer à toutes les opérations de l’esprit en tant qu’elles portent sur des choses « qui ont quelque chose qui puisse se rapporter au corps ». Outre son intérêt intrinsèque, le texte des Regulae peut aussi, je pense, nous inciter à revoir notre jugement sur le projet que Descartes poursuit dans la Géométrie. On a souvent vu dans la Géométrie l’algébrisation de la géométrie, l’acte de naissance de la géométrie analytique, la mise en œuvre d’un projet consistant à remplacer les courbes par leur équation. C’est, bien sûr, en partie, de cela qu’il s’agit. Mais il n’est peut-être pas impossible de soutenir qu’il s’agit d’autre part, comme dans les Regulae, de rendre visible les opérations algébriques, de géométriser l’algèbre. Je voudrais préciser comment, selon les Regulae, l’imagination peut aider l’entendement, et tenter ensuite de monter ce que la Géométrie retient de ce projet.
Le Descartes des Regulae poursuit un projet particulièrement ambitieux : il entend nous donner les moyens d’ordonner toutes les questions qui peuvent être posées à propos des objets qui ont quelque chose de corporel – qu’il s’agisse d’astres, de sons, de lumière, d’aimant, de nombres ou de figures géométriques – puis, après avoir ordonné ces questions en fonction de la difficulté qu’elles présentent, il veut montrer comment il est possible de les traiter en les ramenant à la considération d’une série de rapports qui peuvent être figurés (codés, symbolisés) par des signes, des lettres ou des schémas. Pour Descartes, en effet, toute question qui ne porte pas sur de purs intelligibles peut être ramenée, par abstraction, à la comparaison de certaines grandeurs. Par exemple, on peut étudier comment la hauteur du son que rend une corde vibrante dépend de sa longueur, de son épaisseur et des poids qui la tendent, et il est clair que l’on peut exprimer ces relations par une série de rapports que l’on pourra ensuite représenter par des figures.
- Note de bas de page 4 :
-
Descartes a interrompu la rédaction de son ouvrage. Il prévoyait 36 règles. La règle 18 est la dernière à être rédigée. Nous possédons en outre les titres des règles 19 à 21.
- Note de bas de page 5 :
-
Règles utiles et claires pour la direction de l’esprit et la recherche de la vérité, traduction selon le lexique cartésien et annotation conceptuelle par Jean-Luc Marion avec des notes mathématiques de Pierre Costabel, Martinus Nijhoff, 1977, p. 40.
Précisons sa démarche en nous reportant aux règles 12 à 18 qui constituent, pour nous, la dernière partie du traité4. Le titre de la règle 12 affirme qu’« il faut user de tous les secours qu’apportent l’entendement, l’imagination, le sens et la mémoire, soit pour regarder distinctement les propositions simples, soit pour comparer convenablement les choses qu’on demande avec celles qu’on connaît afin de les reconnaître, soit pour trouver celles que l’on doit rapporter les unes aux autres »5. Il s’agit donc bien de faire jouer toutes les facultés à la fois pour regarder les « propositions simples » et pour considérer les rapports entre les choses (connues et inconnues). Pour comprendre ceci, il faut savoir que, dans tout ce traité, Descartes pense l’ensemble de la connaissance à partir de la considération des rapports qui existent entre les objets. Connaître, c’est ramener toutes les caractéristiques des choses à des rapports entre grandeurs. Ces rapports peuvent être directs, comme dans les « propositions simples » et ils sont alors immédiatement saisis par l’intuition ou indirects, comme c’est le cas dans les raisonnements complexes, qui exigent le recours à la déduction. Intuition et déduction étant, affirme Descartes, les deux seules manières d’accéder à une connaissance certaine. Il y a donc des vérités dont nous pouvons prendre connaissance uno intuitu, d’un seul regard, et d’autres qui exigent que nous en passions par une série d’intermédiaires.
- Note de bas de page 6 :
-
Ibid., p. 61 (Règle 13, AT X, 440). Voir aussi p. 52 (Règle 12, AT X, 427) : « toute la science de l’homme ne consiste qu’à voir distinctement comment ces natures simples concourent ensemble à composer d’autres choses ».
Dans la règle 6, Descartes illustrait ceci à l’aide d’un exemple, celui des proportions et de la recherche des moyennes proportionnelles. Je m’y arrête quelque peu parce qu’il ne s’agit pas seulement d’un exemple, mais aussi du modèle même qui permet à Descartes de penser la manière dont s’ordonnent les connaissances. (I) Descartes envisage d’abord le cas suivant : « Si l’on me donne les grandeurs 3 et 6, je trouverai aisément une troisième en proportion continue, savoir 12 ». Autrement dit, on résout sans difficulté 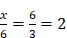 , ou encore
, ou encore 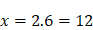 parce que, dans ce cas, il suffit d’« appliquer son attention », comme dit Descartes, à un nombre (6) et à la proportion (2). C’est le cas immédiat, direct. (II) En revanche, continue Descartes, si on donne les deux extrêmes, 3 et 12, on ne peut trouver si aisément la moyenne (6). On a ici « un autre genre de difficulté, tout à fait différent du précédent » parce que, dans ce cas, il faut « appliquer son attention en même temps aux deux extrêmes et à la proportion qu’il y a entre ces deux ». On voit pourquoi les choses se compliquent : il faut à présent prendre en considération trois éléments. Il s’agit de résoudre l’équation suivante :
parce que, dans ce cas, il suffit d’« appliquer son attention », comme dit Descartes, à un nombre (6) et à la proportion (2). C’est le cas immédiat, direct. (II) En revanche, continue Descartes, si on donne les deux extrêmes, 3 et 12, on ne peut trouver si aisément la moyenne (6). On a ici « un autre genre de difficulté, tout à fait différent du précédent » parce que, dans ce cas, il faut « appliquer son attention en même temps aux deux extrêmes et à la proportion qu’il y a entre ces deux ». On voit pourquoi les choses se compliquent : il faut à présent prendre en considération trois éléments. Il s’agit de résoudre l’équation suivante : 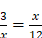 , c’est-à-dire
, c’est-à-dire 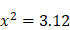 ,
, 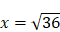 . On a, dans ce cas, une équation à une inconnue du second degré. (III) On peut franchir une étape supplémentaire dans la complexité en considérant des données encore plus éloignées (3 et 24), qui supposent encore plus d’intermédiaires :
. On a, dans ce cas, une équation à une inconnue du second degré. (III) On peut franchir une étape supplémentaire dans la complexité en considérant des données encore plus éloignées (3 et 24), qui supposent encore plus d’intermédiaires : 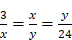 . Ce problème donne lieu aux équations couplées suivantes :
. Ce problème donne lieu aux équations couplées suivantes : 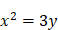 et
et 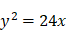 , que l’on peut transformer pour obtenir une équation à une inconnue de degré 3 :
, que l’on peut transformer pour obtenir une équation à une inconnue de degré 3 : 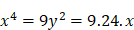 donc
donc 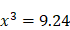 , d’où l’on peut tirer
, d’où l’on peut tirer 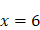 puis, à partir de
puis, à partir de 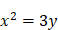 ,
, 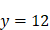 . (IV) On pourrait penser que l’introduction d’un rapport supplémentaire va, à nouveau, compliquer le problème. Ce n’est en fait pas le cas car si l’on cherche les intermédiaires entre 3 et 48 (à savoir 6, 12, et 24) on peut commencer par chercher la moyenne proportionnelle entre 3 et 48, ce qui ramène le problème au cas (II), puis déterminer les deux autres moyennes de la même manière. Dans ce cas, le problème est donc plus simple que celui envisagé au cas précédent. Cette question de la recherche des moyennes proportionnelles est, on le voit, liée à celle de la recherche des solutions des équations de degré de plus en plus élevé. Question essentielle pour Descartes : son projet, lorsqu’il écrit la Géométrie, était de proposer une méthode générale pour résoudre les équations polynomiales de degré quelconque. Mais ce problème mathématique est aussi, je l’ai dit, intéressant en tant que modèle de la connaissance. D’une part, cet exemple manifeste que, s’il faut ordonner les problèmes en fonction de leur difficulté, cet ordre n’est pas toujours celui qui apparaît immédiatement : contrairement à ce que l’on pourrait d’abord penser, le cas IV est plus facile que le cas III. C’est précisément l’un des buts essentiels de la méthode proposée par Descartes que de nous donner les moyens de passer de l’ordre dans lequel les problèmes se présentent à celui selon lequel notre connaissance se construit. D’autre part, cet exemple montre que connaître, c’est essentiellement dégager ce que l’on cherche de l’ensemble des rapports où il est enveloppé. Comme l’écrit Descartes, « toute connaissance qu’on n’acquiert point par le regard (intuitus) simple et pur <pris> d’une chose unique est acquise par la comparaison de deux ou plusieurs termes entre eux. Et certes quasi toute l’industrie de la raison humaine consiste à préparer cette opération »6.
. (IV) On pourrait penser que l’introduction d’un rapport supplémentaire va, à nouveau, compliquer le problème. Ce n’est en fait pas le cas car si l’on cherche les intermédiaires entre 3 et 48 (à savoir 6, 12, et 24) on peut commencer par chercher la moyenne proportionnelle entre 3 et 48, ce qui ramène le problème au cas (II), puis déterminer les deux autres moyennes de la même manière. Dans ce cas, le problème est donc plus simple que celui envisagé au cas précédent. Cette question de la recherche des moyennes proportionnelles est, on le voit, liée à celle de la recherche des solutions des équations de degré de plus en plus élevé. Question essentielle pour Descartes : son projet, lorsqu’il écrit la Géométrie, était de proposer une méthode générale pour résoudre les équations polynomiales de degré quelconque. Mais ce problème mathématique est aussi, je l’ai dit, intéressant en tant que modèle de la connaissance. D’une part, cet exemple manifeste que, s’il faut ordonner les problèmes en fonction de leur difficulté, cet ordre n’est pas toujours celui qui apparaît immédiatement : contrairement à ce que l’on pourrait d’abord penser, le cas IV est plus facile que le cas III. C’est précisément l’un des buts essentiels de la méthode proposée par Descartes que de nous donner les moyens de passer de l’ordre dans lequel les problèmes se présentent à celui selon lequel notre connaissance se construit. D’autre part, cet exemple montre que connaître, c’est essentiellement dégager ce que l’on cherche de l’ensemble des rapports où il est enveloppé. Comme l’écrit Descartes, « toute connaissance qu’on n’acquiert point par le regard (intuitus) simple et pur <pris> d’une chose unique est acquise par la comparaison de deux ou plusieurs termes entre eux. Et certes quasi toute l’industrie de la raison humaine consiste à préparer cette opération »6.
- Note de bas de page 7 :
-
Ibid., pp. 309-313.
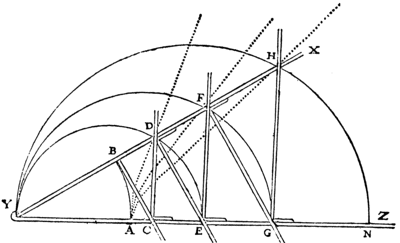
Il n’est pas sans intérêt pour notre propos de noter avec P. Costabel7 que Descartes avait trouvé un moyen tout à fait « visuel », et même mécanique pour déterminer les moyennes proportionnelles : son fameux compas. (Le schéma et l’explication qui suivent sont tirés du livre second de la Géométrie, AT VI, 391-392).
Les branches YX et YZ sont articulées en Y. YX est munie d’une tige perpendiculaire fixée en B. Le reste consiste en une série d’équerres qui peuvent glisser le long de YX et de YZ.
Quand le compas est complètement fermé, les points B, C, D, E, F, G, H coïncident tous avec le point A. À mesure qu’on l’ouvre, la tige fixée en B pousse vers Z la règle CD qui coule sur YZ en faisant toujours un angle droit avec elle ; et CD pousse DE, qui coule tout de même sur YX en demeurant parallèle à BC ; DE pousse EF, EF pousse FG, celle-ci pousse GH, et on en peut concevoir une infinité d’autres. Comme les triangles YBC, YCD, YDE, YEF, etc. sont semblables, on a immédiatement 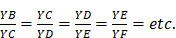 Le dispositif permet, par exemple, de trouver les deux moyennes proportionnelles entre deux grandeurs YB et YE données : il suffit de jouer sur l’ouverture du compas pour que l’équerre DCE viennent s’appuyer en C sur la tige fixée en B. Les deux moyennes cherchées seront YC et YD.
Le dispositif permet, par exemple, de trouver les deux moyennes proportionnelles entre deux grandeurs YB et YE données : il suffit de jouer sur l’ouverture du compas pour que l’équerre DCE viennent s’appuyer en C sur la tige fixée en B. Les deux moyennes cherchées seront YC et YD.
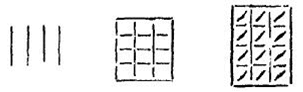
Revenons à la règle 12 et au jeu des différentes facultés. Descartes précise que « seul l’entendement est capable de percevoir la vérité » mais qu’il « doit néanmoins être assisté par l’imagination, le sens, et la mémoire ». Il fait ensuite du rôle de chacune de nos facultés une description très proche de celle qu’en faisait Aristote dans le De anima : l’objet que nous voyons (ou que nous sentons, ou que nous entendons) commence par imprimer sa figure dans le sens externe, comme le cachet dans la cire. Le « corps opaque que l’on rencontre le premier dans l’œil » (mais aussi la première membrane des oreilles, des narines et de la langue) reçoivent une figure nouvelle. On peut, dit Descartes, « considérer que toutes les différences entre les choses sensibles » peuvent être exprimées par des figures. Par exemple, rien n’empêche de concevoir la diversité qui se trouve entre le blanc, le bleu et le rouge, comme celle qui se trouve entre les figures suivantes :
- Note de bas de page 8 :
-
M. Fichant fait remarquer que l’imagination, qu’elle reçoive ses idées ou figures du sens commun ou de la force cognitive, est toujours, du fait de son caractère corporel, passive et réceptrice. Il n’y a pas d’imagination productrice chez Descartes. C’est, dit-il encore, ce qui interdit de confondre l’ingenium avec le schématisme kantien qui s’inscrit pourtant dans sa filiation. M. Fichant, Science et métaphysique dans Descartes et Leibniz, P.U.F., 1998, p. 5, n. 1.
Il ne s’agit bien sûr pas là d’une tentative pour décrire de manière réaliste les figures et les mouvements qui seraient associés à notre sensation des couleurs. Le code proposé ici est tout à fait arbitraire. Il serait, pour Descartes, possible de coder ainsi en des figurae toutes les variations sensibles des choses. Les couleurs ne sont qu’un exemple. Les sons, les odeurs, les saveurs, etc. peuvent, en principe, être eux aussi rapportés à l’ordre figuratif. La figure ainsi imprimée dans le sens externe est ensuite transmise au sens commun puis à l’imagination, qui est elle aussi purement corporelle. Descartes y insiste bien : l’imagination est une « vraie partie du corps », qui possède une certaine étendue, de dimension suffisante pour que plusieurs de ses parties puissent revêtir des figures distinctes les unes des autres et les retenir assez longtemps (ce que l’on appelle « mémoire »). L’imagination peut ensuite mouvoir les nerfs et donc le corps lui-même. Et c’est ainsi, précise Descartes, que l’on peut comprendre les mouvements des animaux et « toutes les opérations que nous accomplissons sans le concours de la raison ». Jusqu’ici, il faut le souligner, nous sommes restés dans le seul registre du corps. Pour les hommes peut ensuite intervenir une « force purement spirituelle », tout à fait distincte du corps. Cette vis cognoscens, si elle s’applique avec l’imagination au sens commun, est dite voir, toucher, etc. ; si elle s’applique à l’imagination comme revêtue de diverses figures, elle est dite se souvenir ; si elle s’applique à l’imagination en tant qu’elle y forge de nouvelles figures, elle est dite imaginer ou concevoir ; si enfin elle agit seule, elle est dite entendre (intelligere). Et cette force est appelée diversement selon ses diverses fonctions : vel intellectus purus, vel imaginatio, vel sensus ; proprie autem ingenium appellatur, cum modo ideas in phantasia novas format, modo jam factis incumbit (on l’appellera proprement esprit, soit qu’il forme de nouvelles idées dans la fantaisie, soit qu’il s’adonne à d’autres déjà faites8). Et le lecteur conclura aisément, poursuit Descartes, « quels secours il faut demander à chacune de ces facultés et jusqu’à quel point l’industrie des hommes se peut étendre pour suppléer aux défauts de l’esprit (ingenium) ».
- Note de bas de page 9 :
-
Règles utiles et claires pour la direction de l’esprit, op. cit., p. 44 (Règle 12, AT X, 417).
L’ingenium, est donc l’esprit aidé par l’imagination, c’est l’esprit en tant qu’il considère les figures déjà présentes dans l’imagination ou en tant qu’il y forme de nouvelles figures. C’est aussi l’esprit qui a besoin de l’imagination pour pallier ses défauts. Il y a là quelque chose d’étonnant au regard de ce que l’on retient en général de la théorie cartésienne de la connaissance. Bien sûr, Descartes affirme ici aussi que si l’entendement (intellectus) s’applique à des choses qui n’ont rien de corporel, il ne peut attendre aucun secours des autres facultés, et qu’il faut même, dans ce cas, s’assurer qu’il ne sera pas empêché par les autres facultés. Mais il estime néanmoins que « si l’entendement se propose d’examiner quelque chose qui puisse se rapporter au corps », il faut en passer par l’imagination et même par les sens externes, en dessinant des figures. Si l’entendement examine quelque chose qui peut se rapporter au corps, « il faut en former une idée, la plus distincte qu’on pourra, dans l’imagination »9. Et pour obtenir plus commodément cette idée, il faudra présenter aux sens externes la chose que cette idée représente. La chose ou plutôt une « figure abrégée » de la chose, de manière à ne point encombrer la mémoire. Ces « figures abrégées » sont des chiffres, des lettres, ou des images.
- Note de bas de page 10 :
-
Ibid., p. 67 (Règle 14, AT X, 447).
- Note de bas de page 11 :
-
Ibid., p. 63 (Règle 14, AT X, 442).
- Note de bas de page 12 :
-
Ibid., p. 66 (Règle 14, AT X, 446).
Les règles 13 et 14 reviennent sur le projet général des Regulae. Il s’agit d’acquérir la connaissance en réduisant des proportions, si emmêlées qu’elles soient, jusqu’à ce que l’égalité entre la chose demandée et quelque chose connue soit vue clairement10. Acquérir une connaissance, c’est dégager le chose que l’on cherche de l’ensemble des rapports où elle est enveloppée ; c’est résoudre une équation du type de celles que nous avons données plus haut. Ceci suppose que nous ayons affaire à des grandeurs. Nous devons donc commencer par ramener nos questions à une série de rapports entre grandeurs. D’autre part, pour que l’imagination puisse aider l’entendement, il faut encore que nous rapportions tout ce que nous savons de ces grandeurs à une grandeur en particulier, l’étendue figurée, qui est le plus facilement dépeinte en notre imagination. Toutes les questions déterminées seront ainsi ramenées à des comparaisons entre grandeurs figurées. Descartes précise encore que l’étendue dont il s’agit ici n’est pas cet « être philosophique » que serait une étendue séparée intellectuellement des corps, car cette dernière ne « tombe pas sous l’imagination »11. C’est donc de l’étendue en tant qu’elle ne se sépare pas des corps qu’il sera question. Et même si l’entendement peut se livrer à toutes sortes d’abstractions et isoler tel ou tel terme, l’imagination doit, quant à elle, « forger la vraie idée de la chose », afin que l’entendement puisse se tourner vers les autres conditions de la chose, et qu’il ne juge pas qu’elles en ont été exclues. Ainsi, l’imagination rappellera à l’entendement qui conçoit une surface comme longue et large, qu’il ne peut s’agir que de la surface d’un corps, qui a aussi une profondeur. Ce que Descartes recommande, en ce qui concerne la mathématique, arithmétique et géométrie, ce n’est pas du tout de s’efforcer d’arracher l’entendement pur à l’imagination. Au contraire, les mathématiciens s’égarent lorsqu’ils renoncent au secours de l’imagination. Ainsi, le géomètre « met de la confusion dans son objet », quand il juge, de manière contradictoire, à la fois que les lignes n’ont aucune largeur et que « la course d’une ligne » peut produire une surface. S’il usait du secours de l’imagination, qui ne permet pas d’oublier que la ligne, comme la surface, est toujours la ligne (ou la surface) d’un corps, il saurait que la ligne dont la course produit la surface est un vrai corps12.
Dans la règle 15 apparaissent les figures qui doivent nous permettre de représenter dans l’étendue n’importe quelle relation entre grandeurs et donc n’importe quelle question déterminée. Descartes introduit là deux genres de figures qui sont, dit-il, les plus simples que l’on puisse imaginer : des réseaux de points pour « faire voir » les multiplicités et des figures géométriques continues (en l’occurrence des lignes et des rectangles) pour faire voir les grandeurs. Cette double figuration est significative : elle est l’expression de l’idée qu’il y a deux genres d’objets irréductibles, les nombres et les grandeurs, et deux domaines différents, le discret et le continu. L’unité sera représentée soit par un carré, soit par une ligne, soit par un point. Pour figurer une grandeur, on utilisera soit un rectangle dont un côté est l’unité et l’autre la grandeur proposée, soit une ligne de la longueur proposée, soit une suite de points. Après que la règle 15 a introduit ces figures, la règle 16 suggère que l’on peut, lorsque l’on n’opère pas sur les grandeurs, mais que l’on veut seulement les noter pour soulager notre mémoire, représenter les grandeurs ou les multiplicités de manière encore plus concise, par une seule lettre. Cependant, lorsqu’il introduit les opérations, Descartes reprend les figures introduites précédemment. La règle 18 propose un schématisme très simple pour l’addition (on obtient la ligne représentant a + b en dessinant l’une à la suite de l’autre la ligne représentant a et la ligne représentant b), pour la soustraction (on obtient la ligne représentant a – b en dessinant la ligne représentant a et la ligne représentant b l’une en dessous de l’autre puis en reproduisant la portion de la première qui n’est pas doublée par la seconde) et pour la multiplication (le produit a.b sera figuré par un rectangle dont la longueur et la largeur seront les lignes représentant a et b). En ce qui concerne la division, dans laquelle le diviseur est donné, on imaginera, écrit Descartes, que la grandeur à diviser est un rectangle dont un côté est le diviseur et l’autre le quotient. On pourrait s’étonner que Descartes introduise ce schématisme qui semble totalement inutile. On ne verra, je pense, l’intérêt d’un tel projet qu’en se reportant à la Géométrie. S’il est essentiel, pour Descartes, d’associer une figure géométrique à chaque opération algébrique, c’est qu’il veut pouvoir utiliser les figures géométriques pour résoudre des questions algébriques. Il faut cependant reconnaître que le schématisme développé ici est totalement inutilisable (et restera d’ailleurs inutilisé). Le fait que la multiplication amène à passer des lignes aux rectangles constitue une première limite, parce que cela rend problématique la réitération de l’opération (il faudrait en effet passer à des objets à 3, puis 4, etc. dimensions). De plus, ce schématisme ne permet pas de traiter le cas de l’extraction de la racine. Or cette opération est indispensable pour résoudre les problèmes que Descartes se propose : même dans le cas simple où l’on cherche une seule moyenne proportionnelle, cas qui correspond à une équation du type 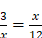 , on est amené à utiliser l’extraction de racine. Descartes a très certainement aperçu les limites de ce schématisme et ce n’est sans doute pas par hasard que son traité s’arrête ici.
, on est amené à utiliser l’extraction de racine. Descartes a très certainement aperçu les limites de ce schématisme et ce n’est sans doute pas par hasard que son traité s’arrête ici.
- Note de bas de page 13 :
-
M. Fichant, op. cit., p. 8.
- Note de bas de page 14 :
-
Ibid., p. 10.
- Note de bas de page 15 :
-
Ibid., p. 20.
- Note de bas de page 16 :
-
Ibid., p. 61.
Le projet des Regulae, est, comme l’écrit M. Fichant, celui d’une « réduction méthodologique à l’étendue »13. Toute connaissance que l’on ne peut pas acquérir immédiatement par l’intuition est instauration et comparaison de rapports. Tous ces rapports peuvent être exprimés par des grandeurs qui seront figurés dans l’étendue. L’étendue sera donc signe de toutes les autres grandeurs. Connaître, pour les Regulae, cela revient à substituer au réel un code (fondé sur la représentation au moyen de lignes plus ou moins longues, mais aussi de figures et de chiffres). C’est cela que devrait réaliser l’ingenium. On a donc « un double mouvement d’abstraction puis de symbolisation »14. L’abstraction ou réduction consiste à ramener toute question (qu’il s’agisse de questions mathématiques, ou des sons et des couleurs, par exemple) à la grandeur en général, à une série de proportions. La symbolisation consiste à transposer dans l’étendue, sous forme de figures, les rapports et proportions ainsi isolés. Mais le programme que Descartes expose dans les Regulae ne sera jamais réalisé. À l’époque du Discours, Descartes a renoncé à géométriser la physique. Quoiqu’il déclare que « toute sa physique est géométrie », Descartes n’a pas à proprement parler développé de physique mathématique. Comme le souligne M. Fichant, la physique cartésienne n’est autre chose que géométrie en ce sens seulement que les corps ne sont rien d’autre que de l’étendue. C’est là une affirmation qui appartient à la métaphysique, qui porte sur l’être de ce que nous appelons la « réalité physique » ; il ne s’agit pas de mettre la physique en équation et de la ramener aux mathématiques. La physique de Descartes, écrit encore Fichant « ne tire aucun bénéfice des procédures de symbolisation et de mise en équation des Regulae »15. Et il rappelle le jugement de Bachelard : « la physique de Descartes n’appartient nullement, dans l’acception moderne du terme, à ce qu’on appelle la physique mathématique… Laissons donc la physique de Descartes dans sa solitude historique »16.
Descartes a abandonné le projet « physico-mathématique » des Regulae. Mais, en mathématique même, il n’a pas renoncé à l’idée qu’il fallait pouvoir figurer les rapports et les opérations. Sa Géométrie manifeste qu’il continue à penser que, comme le dit Rabouin, en mathématique on a accès à la conceptualité par l’intermédiaire des diagrammes.
La Géométrie de 1637
- Note de bas de page 17 :
-
Selon l’expression de A. Warsufel, dont la « Présentation de la Géométrie » (Descartes, Œuvres complètes, sous la direction de Jean-Marie Beyssade et Denis Kambouchner, Gallimard, coll. Tel, 2009, t. III, pp. 397-398) est particulièrement éclairante pour la question qui nous occupe : « La relation entre les deux disciplines [algèbre et géométrie] est assez complexe. D’un côté, la géométrie est soumise à l’algèbre, car tout problème la concernant est désormais (théoriquement) ramené à une simple vérification sur des nombres : c’est le point de vue traditionnel sur l’invention de la géométrie cartésienne. Mais d’un autre côté, la géométrie rend un service inestimable à l’algèbre en réglant le dernier problème des mathématiques : expliciter graphiquement les racines d’un polynôme arbitraire. En retour, l’algèbre conquérante paie ses dettes à la géométrie, permettant de répondre à toutes les questions que pose une courbe, comme sa construction point par point à partir de son équation, ou l’algorithme de détermination de ses tangentes […] qui apporte la brillante solution à une importante question d’optique ».
Descartes affirme qu’avec la Géométrie il a achevé les mathématiques. Sans doute parce qu’il pense avoir donné une solution complète à ce qui était, selon lui, le dernier problème important qui restait posé aux mathématiciens : trouver une méthode générale pour résoudre les équations algébriques, c’est-à-dire, trouver une méthode générale pour obtenir les racines d’un polynôme de degré quelconque. Précisons d’emblée que Descartes a été quelque peu présomptueux : la méthode qu’il propose ne fonctionne que jusqu’au 6e degré. Mais ce qui me semble important pour notre propos est de noter que c’est par une méthode graphique que Descartes va résoudre ce problème : il va donner le moyen de construire une ligne dont la longueur est égale à la racine en question. Ceci doit peut-être nous amener à nous interroger sur le décalage qu’il y a entre les raisons pour lesquels nous jugeons ce traité précieux, et les raisons pour lesquelles Descartes lui-même l’estimait important. Nous avons tendance à voir avant tout dans ce texte l’acte de naissance de la géométrie analytique : Descartes aurait trouvé le moyen de ramener tout problème géométrique à un calcul, il aurait « placé la géométrie sous l’autorité définitive de l’algèbre »17. Or peut-être que Descartes lui-même ne voyait pas les choses comme cela. Lorsqu’il introduit ce que nous désignons aujourd’hui comme les coordonnées cartésiennes dans le cadre de la résolution du fameux problème de Pappus, Descartes le fait de manière extrêmement discrète, et on ne peut certainement pas attribuer cela à un excès de modestie, qui ne serait vraiment pas dans sa manière. En réalité, Descartes n’avait sans doute pas saisi l’importance de cette technique dont nous considérons qu’elle permet de remplacer les figures par des équations voire de se passer complètement des figures. Et peut-être l’une des raisons pour lesquelles Descartes ne mesure pas l’intérêt de sa méthode est-elle que, précisément, il ne juge pas souhaitable de se passer des figures. Pour lui, les coordonnées que nous appelons cartésiennes sont plutôt un outil, une technique, et pas une méthode qui devrait révolutionner l’esprit dans lequel travaille le géomètre (ce qu’elles deviendront par la suite). Il faut aussi être attentif à ceci que, pour Descartes, les fameuses coordonnées sont toujours des longueurs de segment. Elles sont donc toujours positives. Ceci complique considérablement leur utilisation, mais c’est le prix à payer pour pouvoir continuer à interpréter géométriquement (visuellement) ces coordonnées. Peut-être que, pour Descartes, il s’agit d’abord de montrer comment la géométrie permet de traiter ce grand problème de l’algèbre qu’est la recherche des racines d’un polynôme. Nous sommes tentés de voir dans ce traité une algébrisation de la géométrie. Il n’est peut-être pas impossible d’y voir une géométrisation de l’algèbre. Et il est en tout cas difficile de préciser ce que Descartes lui-même y voyait. La question est d’autant plus épineuse que le plan de la Géométrie n’est pas linéaire : la question centrale est, on l’a dit, la résolution générale des équations algébriques, et c’est d’une résolution graphique qu’il s’agit. Mais Descartes traite aussi des problèmes qui ne participent pas ou pas directement à ce projet principal, et que l’on pourrait interpréter comme des illustrations de la puissance de l’algèbre pour résoudre des questions géométriques. C’est le cas de la résolution complète du problème de Pappus pour lequel il introduit les fameuses coordonnées, et que l’on peut considérer comme un exercice de géométrie analytique, ou de la résolution du problème des tangentes, qu’il traite aussi grâce à l’algèbre.
Les premières pages de la Géométrie sont consacrées à présenter un schématisme efficace pour la multiplication, la division et l’extraction de racine (les cas de l’addition et de la soustraction, évidents, ne sont pas exposés). Descartes va traduire géométriquement les opérations de base.
- Note de bas de page 18 :
-
Descartes, Œuvres complètes, op. cit., p. 416.
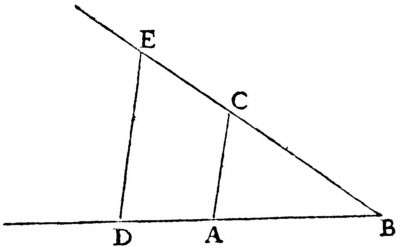
Pour la multiplication : « Soit, par exemple, AB l’unité, et qu’il faille multiplier BD par BC, je n’ai qu’à joindre les points A et C, puis tirer DE parallèle à CA, et BE est le produit de cette multiplication »18.
Le théorème de Thalès permet en effet d’écrire 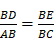 , d’où on tire immédiatement le résultat annoncé, puisque AB est l’unité.
, d’où on tire immédiatement le résultat annoncé, puisque AB est l’unité.
- Note de bas de page 19 :
-
Id.
Pour la division : « s’il faut diviser BE par BD, ayant joint les points E et D, je tire AC parallèle à DE, et BC est le produit de cette division »19. Le schéma est le même que pour la multiplication. On a en effet 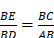 .
.
- Note de bas de page 20 :
-
Id.
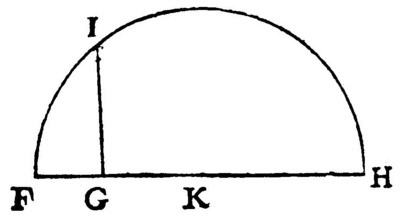
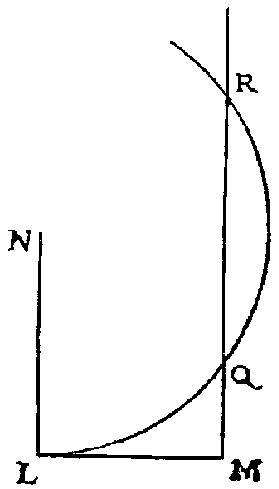
Pour l’extraction de la racine carrée : « s'il faut tirer la racine carrée de GH, je lui ajoute en ligne droite FG, qui est l'unité, et divisant FH en deux parties égales au point K, du centre K je tire le cercle FIH, puis élevant du point G une ligne droite jusqu'à I à angles droits sur FH, c'est GI la racine cherchée »20.
En effet : les triangles FIG et IGH sont semblables. On a donc 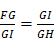 . La conclusion est immédiate, puisque FG est l’unité.
. La conclusion est immédiate, puisque FG est l’unité.
Après cette figuration des opérations de l’algèbre, Descartes montre comment on peut déterminer graphiquement les solutions d’une équation du second degré.
- Note de bas de page 21 :
-
Ibid., p. 419.
Par exemple, si l’équation est du type 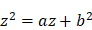 , on procède comme suit : « je fais le triangle rectangle NLM, dont le côté LM est égal à b, racine carrée de la quantité connue b2, et l’autre LN est
, on procède comme suit : « je fais le triangle rectangle NLM, dont le côté LM est égal à b, racine carrée de la quantité connue b2, et l’autre LN est  , la moitié de l’autre quantité connue qui était multipliée par z, que je suppose être la ligne inconnue ; puis prolongeant MN, la base de ce triangle, jusqu’à O, en sorte que NO soit égale à NL, la toute OM est z, la ligne cherchée ; et elle s’exprime en cette sorte :
, la moitié de l’autre quantité connue qui était multipliée par z, que je suppose être la ligne inconnue ; puis prolongeant MN, la base de ce triangle, jusqu’à O, en sorte que NO soit égale à NL, la toute OM est z, la ligne cherchée ; et elle s’exprime en cette sorte : 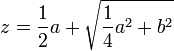 21.
21.
Cette équation, nous le savons, possède deux solutions. Il est remarquable que Descartes s’en tienne à la solution positive, la seule qui peut être interprétée comme la longueur d’un segment.
- Note de bas de page 22 :
-
Id.
Descartes envisage ensuite le cas de l’équation 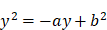 . Pour nous, qui considérons spontanément a comme une quantité algébrique, qui peut être positive ou négative, ce cas est identique au précédent. Pas pour Descartes, pour qui toutes les lettres désignent des « lignes », des longueurs. Il adapte son raisonnement : « je fais le même triangle rectangle NLM, et de sa base MN j’ôte NP égale à NL, et le reste PM est y, la racine cherchée. De façon que j’ai
. Pour nous, qui considérons spontanément a comme une quantité algébrique, qui peut être positive ou négative, ce cas est identique au précédent. Pas pour Descartes, pour qui toutes les lettres désignent des « lignes », des longueurs. Il adapte son raisonnement : « je fais le même triangle rectangle NLM, et de sa base MN j’ôte NP égale à NL, et le reste PM est y, la racine cherchée. De façon que j’ai 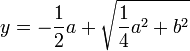 »22. À nouveau, Descartes s’en tient à la solution positive.
»22. À nouveau, Descartes s’en tient à la solution positive.
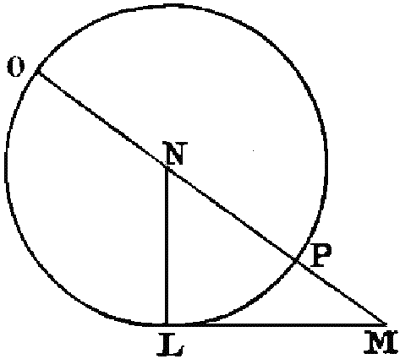
Descartes traite ensuite l’équation 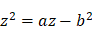 . Dans ce cas on peut avoir affaire à des racines imaginaires (précédemment, la quantité qui se trouvait sous le radical était toujours positive ; ici, elle peut être négative). Descartes nous fait voir, en construisant le dessin que, dans certains cas, il ne pourra pas y avoir de racine :
. Dans ce cas on peut avoir affaire à des racines imaginaires (précédemment, la quantité qui se trouvait sous le radical était toujours positive ; ici, elle peut être négative). Descartes nous fait voir, en construisant le dessin que, dans certains cas, il ne pourra pas y avoir de racine :
- Note de bas de page 23 :
-
Ibid., p. 420.
« je fais NL égale à 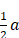 , et LM égale à b comme devant, puis ; au lieu de joindre les points MN je tire MQR parallèle à LN, et du centre N, par L, ayant décrit un cercle qui la coupe aux points Q et R, la ligne cherchée z est MQ, ou bien MR, car en ce cas elle s’exprime en deux façons, à savoir
, et LM égale à b comme devant, puis ; au lieu de joindre les points MN je tire MQR parallèle à LN, et du centre N, par L, ayant décrit un cercle qui la coupe aux points Q et R, la ligne cherchée z est MQ, ou bien MR, car en ce cas elle s’exprime en deux façons, à savoir 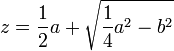 et
et 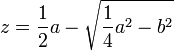 »23.
»23.
- Note de bas de page 24 :
-
Id.
Dans ce cas, Descartes donne les deux racines, parce qu’elles sont toutes deux positives et qu’elles ont donc l’une et l’autre une interprétation géométrique. Il précise cependant qu’il pourrait arriver qu’il n’y ait pas de racines : « Et si le cercle, qui ayant son centre au point N, passe par le point L, ne coupe ni ne touche la ligne droite MQR, il n’y a aucune racine en l’équation, de façon qu’on peut assurer que la construction du problème proposé est impossible »24. Cela arrivera si 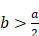 .
.
Descartes s’attaque ensuite une première fois au théorème de Pappus. Le cas qu’il va traiter explicitement est le cas à 4 droites, mais il annonce aussi les résultats que l’on obtient pour un plus grand nombre de droites.
- Note de bas de page 25 :
-
La géométrie analytique nous permet de résoudre rapidement ce problème : nous savons que la distance d’un point de coordonnées (u,v) à la droite d’équation ax+by+c=0 n’est autre que . De là, nous concluons très facilement que le lieu du point C est une courbe du second degré (ici en (u, v) qui sont les coordonnées du point C), une conique.
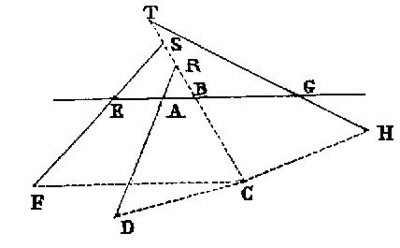
Dans le cas particulier qui est ici traité, la question est la suivante : on donne quatre droites (ici en traits pleins). On demande le lieu d’un point C tel que les segments (en pointillés) menés de ce point C à chacune des droites suivant des directions déterminées ont des produits égaux, ici CB × CF = CD × CH. Les lignes en pointillés doivent faire un angle déterminé avec les droites données. Si on considère le cas particulier où tous ces angles sont de 90°, le théorème de Pappus devient : Quel est le lieu d’un point C tel que le produit des distances de ce point à deux droites données soit égal au produit des distances de ce point à deux autres droites données : 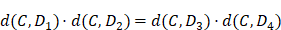 25. Que l’on ait, dans le cas général, une sorte de « distance oblique » ne modifie en fait pas fondamentalement le problème.
25. Que l’on ait, dans le cas général, une sorte de « distance oblique » ne modifie en fait pas fondamentalement le problème.
C’est dans la résolution de ce problème que Descartes introduit ce que nous appelons aujourd’hui les coordonnées cartésiennes. Comme nous l’avons signalé ci-dessus, les valeurs x et y en question sont ici des longueurs particulières, par rapport auxquelles les autres longueurs sont déterminées. Il s’agit donc nécessairement de quantités positives, ce qui, bien sûr, rend leur manipulation compliquée.
Reprenons le texte de Descartes
- Note de bas de page 26 :
-
Descartes, Œuvres complètes, op. cit., p 425.
Premièrement, je suppose la chose comme déjà faite, et pour me démêler de la confusion de toutes ces lignes, je considère l’une des données et l’une de celles qu’il faut trouver, par exemple AB et CB, comme les principales ; et auxquelles je tâche de rapporter ainsi toutes les autres. Que le segment de la ligne AB, qui est entre les points A et B, soit nommé x ; et que BC soit nommé y ; et que toutes les autres lignes données soient prolongées jusqu’à ce qu’elles coupent ces deux, aussi prolongées, s’il est besoin et si elles ne leur sont point parallèles ; comme vous voyez ici qu’elles coupent la ligne AB aux points A, E, G, et BC aux points R, S, T »26.
- Note de bas de page 27 :
-
Ibid. p. 711.
Descartes introduit ici les deux grandeurs de référence, x et y. Nous ne pouvons pas nous empêcher de voir AB et la parallèle à CB passant par A comme les deux axes cartésiens, mais c’est sans y insister que Descartes introduit ces coordonnées. Comme le dit Warsufel, « ce serait une erreur de croire en l’occurrence à une discrétion faite d’orgueilleuse dissimulation. L’introduction des coordonnées n’était nullement aux yeux de Descartes le concept fondamental de la révolution introduite, mais seulement son outil privilégié »27.
La suite du développement — que je ne reprends pas dans le détail — consiste à utiliser les propriétés des triangles semblables pour parvenir à exprimer les grandeurs CB, CD, CF et CH, qui interviennent dans la thèse, en fonction des grandeurs x et y et d’une série de grandeurs connues qui dépendent des positions des quatre droites données et des angles que les segments tirés de C font avec ces quatre droites. Une fois parvenu à ce stade, il ne reste plus qu’à constater que chacune des grandeurs CB, CD, CF et CH ne fait intervenir x et y qu’au premier degré, et que, par conséquent, l’expression de la condition à laquelle doit satisfaire le point C ne fera intervenir que du second degré en les inconnues x et y, ce qui revient à dire que le lieu cherché est une conique.
Descartes donne ensuite des indications concernant la résolution du problème de Pappus à un plus grand nombre de droites. Dans le cas du problème à 6 droites, on aura une équation de degré 3. De manière générale, les lieux à 2n droites et à 2n-1 droites sont des courbes algébriques de degré n, définies par des polynômes de degré n de la forme Pn(x,y) = 0. Cela donne lieu à une classification des courbes algébriques en fonction du nombre de droites auquel elles correspondent dans le problème de Pappus. Classer ainsi les courbes en fonction du nombre de droites de Pappus, c’est aussi, bien sûr, les classer en fonction de leur équation. On pourrait voir là un indice que Descartes cherche à soumettre la géométrie à l’algèbre, alors qu’un développement tel que l’interprétation graphique de la résolution des équations du second degré, que nous avons évoqué ci-dessus, manifesterait plutôt l’importance de la visualisation des questions algébriques. En parcourant les deux autres livres de la Géométrie, on constate que ce va-et-vient entre algébrisation de la géométrie et géométrisation de l’algèbre se poursuit tout au long du traité.
Leibniz
On pourrait penser que Leibniz, si souvent salué par les mathématiciens et les logiciens formalistes du début du XXe siècle comme leur précurseur, soit plus encore que Descartes, convaincu que la mathématique peut, ou même doit, se faire sans recours aux images. Y. Belaval, l’un des grands commentateurs de Leibniz, opposait ainsi l’intuitionnisme cartésien au formalisme leibnizien. Et il insistait sur le rôle important que jouait chez Leibniz la « pensée aveugle », cette pensée qui manipule les symboles sans voir - sans saisir par l’intuition - les idées que ces symboles représentent. Selon cette interprétation, la certitude des mathématiques, leur puissance et donc leur privilège, tiendrait, pour Leibniz, à leur caractère purement formel, au fait qu’elles ne traiteraient, comme la logique, que de structures sans contenu.
- Note de bas de page 28 :
-
C.I. Gerhardt, Die philosophischen Schriften von G.W. Leibniz, Berlin, 1875-1890 (cite GP ci-dessous) VI, pp. 499-508.
- Note de bas de page 29 :
-
Elles sont confuses, parce qu’on ne peut pas les expliquer. On peut les reconnaître (on peut reconnaître telle ou telle odeur) mais on ne peut pas expliciter ce qu’elles comprennent ; c’est, écrit Leibniz, un « je ne sais quoi dont on ne saurait rendre compte ». Une définition telle que celle que les essayeurs ont de l’or est, en revanche distincte, parce qu’elle précise les marques qui permettent distinguer l’or de tout autre métal. On peut ainsi donner à quelqu’un qui n’a jamais vu d’or le moyen de le reconnaître alors qu’on ne peut pas faire comprendre ce qu’est le rouge à un aveugle.
- Note de bas de page 30 :
-
GP VI, 501.
- Note de bas de page 31 :
-
« Logique, mathématique et imagination dans la philosophie de Leibniz », Corpus, 49, 2005, p. 180.
- Note de bas de page 32 :
-
GP VI, 502.
Contre cette interprétation, qu’il juge anachronique dans sa manière d’insister sur le caractère purement conceptuel et non intuitif des mathématiques, Rabouin soutient que, pour Leibniz, ce qui fait la puissance et la certitude des mathématiques, ce n’est pas le caractère purement formel de leurs raisonnements, mais la nature de leurs objets. Et ces objets sont décrits par le type de connaissance qu’ils réclament : l’imagination, une imagination qui comprend des notions claires et distinctes. À l’appui de cette thèse, Rabouin allègue notamment une longue lettre à Sophie-Charlotte écrite en 170228. Dans un passage qui n’est pas sans rappeler la règle XII dont j’ai déjà parlé ci-dessus, Leibniz commence par évoquer les données des sens externes (les sons, les couleurs, les odeurs), qui sont confuses ou, comme il le dit aussi « occultes », puis il ajoute que les sens nous font aussi connaître « des qualités plus manifestes qui fournissent des notions plus distinctes ». Ces notions plus distinctes sont, par exemple « les nombres et les figures » (on reconnaît les objets de la mathématique), qui peuvent être atteintes par plusieurs sens (vue, toucher, voir ouïe en ce qui concerne les nombres) et qui, pour cela, relèvent d’un « sens commun ». Leibniz poursuit en disant que l’imagination comprend à la fois les notions des sens particuliers, qui sont confuses29, et celles du sens commun, qui sont claires et distinctes. Et il précise que « ces idées claires et distinctes qui sont sujettes à l’imagination sont les objets des sciences mathématiques ». Bien sûr, Leibniz ajoute que les sens et l’imagination ne suffisent pas pour assurer à la mathématique sa généralité : on ne pourrait aller au-delà de l’observation et de l’induction (qui ne permettent pas d’atteindre des vérités générales et nécessaires) si « quelque chose de plus haut, et que l’intelligence seule peut fournir, ne venait au secours de l’imagination et des sens »30. N’empêche que si, dans le domaine des mathématiques, l’imagination n’est pas suffisante, ce texte suggère clairement qu’elle est nécessaire. Et Rabouin affirme que Leibniz serait parvenu avant Kant à « l’idée que l’imagination mathématique appuie en dernière instance la médiation du sensible à l’intelligible »31. Leibniz ne bannit pas l’imagination des terres mathématiques. Il ne faut pas s’en tenir à l’opposition que nous sommes parfois tentés de faire entre un entendement clair et distinct et une imagination vouée à la confusion et qu’il faudrait dès lors écarter. La lettre à Sophie-Charlotte fait place à une imagination distincte. Plus précisément, Leibniz y distingue trois types de notions : sensibles seulement (objets affectés par les sens particuliers), sensibles et intelligibles (qui appartiennent au sens commun), intelligibles seulement (propres à l’entendement). Les premières et les secondes sont imaginables. Les secondes et les troisièmes sont intelligibles et distinctes tandis que les premières sont confuses. Les objets des mathématiques relèvent des secondes notions. Ils sont donc à la fois imaginables, intelligibles et distincts32.
Rabouin fait aussi référence à un opuscule de 1686 dans lequel Leibniz affirme de manière explicite que le privilège des mathématiques est lié au fait que la vérité peut y être « exposée sous les yeux », examinée par l’expérience et guidée par un « fil sensible » :
- Note de bas de page 33 :
-
Eléments de la raison, texte de 1686. G.W. Leibniz, Recherches générales sur l’analyse des notions et des vérités, Introduction et notes par J.-B. Rauzy, P.U.F., 1998, pp. 143-144. Cité par D. Rabouin, « Logique, mathématique et imagination dans la philosophie de Leibniz », p. 178.
Sans doute la raison n’est-elle pas mystérieuse, qui explique qu’à ce jour seules les disciplines mathématiques aient été parées – jusqu’à exciter l’étonnement et la jalousie – non seulement de la certitude mais aussi d’une abondance de vérités éminentes. […] on doit l’attribuer à la nature de l’objet, où la vérité peut être exposée sous les yeux sans grand labeur, sans expérience dispendieuse, […] où se découvre une certaine suite, et pour ainsi dire le fil de la pensée. […]33
- Note de bas de page 34 :
-
Ibid., p. 145. Cité par D. Rabouin, « Logique, mathématique et imagination dans la philosophie de Leibniz », p. 178, n° 29.
Cet avantage d’un examen continuel par l’expérience, et ce fil sensible dans le labyrinthe de la pensée, tel qu’il peut être perçu par les yeux et comme touché de la main (avantages auxquels sont redevables d’après moi les progrès des mathématiques) a manqué jusqu’ici dans les autres domaines de la raison humaine. Car les expériences dans les matières physiques sont difficiles, dispendieuses et trompeuses ; douteuses et périlleuses dans les matières morales et civiles […] ; mais dans les matières métaphysiques elles ne sont, en grande partie, pas mêmes possibles.34
Les mathématiques doivent donc être distinguées de la physique, de la morale et de la métaphysique. Mais elles doivent aussi être distinguées de la logique. Comme science des choses imaginables, la mathématique ne peut être identifiée à la logique. Selon Rabouin, on aurait trop tendance à rabattre l’une sur l’autre ; il y a toujours, dans la mathématique de Leibniz, couplage entre l’aspect algorithmique, formel, et l’aspect intuitif et non disparition du second au seul profit du premier.
- Note de bas de page 35 :
-
G.W. Leibniz, Opuscules philosophiques choisis, traduits du latin par P. Schrecker, Vrin, 1978, pp. 9-16.
De plus, le recours au formalisme, à la « pensée aveugle » ne signifie pas, pour Leibniz, que l’on donne congé au sensible, à l’image. Bien au contraire. Ce thème est notamment développé dans les Méditations sur la connaissance, la vérité et les idées35, que je paraphrase ici. Le plus souvent, explique Leibniz, surtout si l’analyse est très longue, nous n’embrassons pas toute la nature de la chose à la fois ; nous substituons alors aux choses des signes dont, pour abréger, nous avons coutume d’omettre l’explication dans le travail actuel de la pensée, sachant ou croyant que cette explication est en notre possession. Suit l’exemple du chiliogone : je ne considère pas toujours ce qu’est un côté, une égalité, le nombre mille, mais je me sers de ces mots pour qu’ils tiennent lieu des idées que j’ai de ces choses parce que j’ai conscience de posséder la signification de ces mots et que j’estime que l’explication n’en est pas nécessaire pour le moment. C’est la connaissance aveugle ou symbolique. L’introduction de la cogitatio caeca n’est donc pas pensée par Leibniz comme un recours à l’abstraction et au formalisme pour pallier à la confusion des images (comme je ne puis pas imaginer le chiliogone, je lui substitue une idée abstraite) mais comme un recours à des signes sensibles pour pallier à notre incapacité à saisir l’idée (je substitue les signes – ici les mots – aux idées). Un peu paradoxalement, peut-être, croire à l’importance de la cogitatio caeca c’est aussi croire à l’importance du recours au sensible. Les caractères, les signes, les symboles sont essentiellement sensibles. Finalement, ce n’est peut-être pas tant parce qu’on a attribué trop d’importance à la caractéristique que l’on a oublié l’importance du rôle de l’imagination chez Leibniz, mais plutôt parce que l’on a oublié que la caractéristique est affaire de signes sensibles, visibles, d’images.
- Note de bas de page 36 :
-
D. Rabouin, Mathesis universalis, p. 354.
Il va de soi que les quelques indications rassemblées ici ne valent pas démonstration, ne serait-ce que parce que je n’ai allégué que quelques textes de Leibniz, alors qu’il y en a un nombre considérable sur ces questions, et qui peuvent se prêter à des interprétations diverses. Il me semble néanmoins précieux de suggérer que l’interprétation intellectualiste de la conception leibnizienne (mais aussi cartésienne) des mathématiques n’est pas la seule possible : peut-être, après tout que, pour les Classiques, ce qui donne leur solidité aux mathématiques, ce n’est pas que l’on pourrait s’y passer de l’imagination, mais que les objets considérés sont tels que l’imagination peut s’y appliquer dans la clarté et la distinction, non dans la confusion. Peut-être que c’est à raison que Rabouin suggère que, pour les Classiques, les mathématiques ne sont pas seulement un enchaînement de concepts mais la mobilisation d’un lieu – l’espace – où ces enchaînements se donnent à voir. Peut-être que c’est à raison qu’il juge contestable la conception logicisante de l’histoire des mathématiques que l’on a pu développer au début du XXe siècle et pour laquelle la référence kantienne à l’intuition spatiale serait une parenthèse malheureuse : « peut-être que, comme il le suggère, Kant, en liant les mathématiques à l’imagination n’instaure nulle rupture, mais se coule dans une détermination qui domine chez les auteurs classiques36 ».