Images et diagrammes des objets et de leurs transformations dans l’espace¹

« J’aime les choses qui bougent, les choses flexibles que je peux transformer à ma façon »
R. Thom, Paraboles et catastrophes, 1983.

1. Introduction : les divers statuts de l’image

Dans ces qui suit, on distinguera d’abord entre différents types d’objets et d’images qui sont censés les représenter, et notamment entre l’objet représenté dans et par l’image, et l’« objet-représentation » devenu un objet autonome dont la fonction de représentation s’est déplacée sur un autre niveau de signification. De la sorte, cet objet-représentation est capable de représenter des catégories d’objets ou des univers sémantiques autres que les objets qu’on appellera de « premier degré », c’est-à-dire ces objets reflétés dans l’image et dont on exige seulement qu’elle restitue une correspondance fidèle entre la réalité et sa figuration.

On cherchera ensuite à montrer que, pour que l’image devienne elle-même objet de représentation, c’est-à-dire un univers sémantique qui exhibe ou déploie de nouvelles relations et structures sémiotiques, et par conséquent des éléments de connaissance nouveaux par rapport à l’image et à l’objet ou aux objets qu’elle représente, il faut qu’elle acquière le statut d’une « forme » (gestalt) dont toute fonction (prétendue simple) de correspondance ou de figuration fidèle de la réalité est abandonnée au profit d’une production inventive de réalité. Cela devient possible grâce en particulier à l’une des caractéristiques fondamentales que présente la forme, qui est que ses principaux composants (ou éléments constitutifs) illustrent, par un processus d’idéation et d’intuition créatrice, des propriétés essentielles du processus réel que l’on cherche à se représenter. L’ultime but de cette opération est naturellement d’arriver à mieux comprendre le(s) comportement(s) du processus.

On illustrera cette question importante des différents statuts de l’image et de la représentation par trois exemples empruntés aux sciences physico-mathématiques et à la psychophysiologie de la perception.

2. Le niveau symbolique de la perception et la structure des théories physico-mathématiques

Dans le premier exemple, on montrera la nécessité de parler d’un niveau symbolique et/ou scientifique de la perception. Celui-ci prolonge la perception au-delà des limites physiologiques et physiques, et elle est fondamentale en vue de connaître les structures invisibles (par exemple, microscopiques comme les atomes et les molécules) ou les phénomènes à très grande échelle ne pouvant pas être perçus directement (par exemples, les astres et les galaxies très lointaines). Ainsi, les interactions électromagnétiques sont si faibles qu’aussi bien à l’échelle cosmique qu’à celle macroscopique un coup d’œil jeté sur le système physique n’aura aucun effet sur lui. Ici interviennent de façon fondamentale la théorisation conceptuelle et les modèles abstraits. Les yeux du corps et les images rétiniennes sont en fait remplacés par les « yeux et les images de l’esprit », dont dépend non pas (ou non pas seulement) ce qui peut être actuellement vu, mais aussi ce qui devrait ou pourrait être vu.

C’est dire que le propos de toute théorisation scientifique véritable consiste à extraire les propriétés apparentes (observables) des phénomènes à partir de leurs mécanismes de transformation sous-jacents. On peut dire que la principale tendance des sciences expérimentales modernes, et de façon encore plus marquée aujourd’hui, a été de privilégier le besoin d’une description (plus ou moins exhaustive) du visible et de reléguer en second plan la question de la compréhension de l’invisible. À ce propos, René Thom a fait des remarques très intéressantes :

Dans ce contexte, l’image n’a plus aucune fonction de figuration, et ce n’est pas sa plus au moins grande ressemblance à la réalité qui lui confère un pouvoir de description ou d’explication, mais bien plutôt sa capacité de se représenter ou de s’imaginer les processus et les phénomènes physiques au-delà de leurs apparences visibles. L’image se trouve ainsi entièrement « sémiotisée », car elle renvoie désormais à des modèles abstraits et à des structures de relations sémantiques d’où émerge un autre niveau de réalité avec ses propres propriétés et comportements que l’on suppose, en définitive, avoir une existence effective.

Pour rester dans notre exemple emprunté à la physique des particules, ce type de vision doit être capable de « voir » dans l’espace de phase de la mécanique, dans l’espace des événements élémentaires de la théorie probabiliste, dans l’espace-temps courbe et à quatre dimensions de la relativité générale, dans l’espace projectif complexe de dimension infinie de la théorie quantique. Pour comprendre ce qui est visible aux « yeux réels », nous devons savoir qu’il s’agit uniquement de la projection sur la rétine d’une section ou de la silhouette d’un univers à un nombre très grand ou infini de dimensions. Or précisément l’image, conçue au sens habituel et figuré du terme, ne peut pas rendre compte d’un tel univers. Il a fallu ainsi inventer un répertoire de formes (modèles, diagrammes, graphes, dessins, etc.) pour décrire et expliquer cet univers et ses propriétés. Ce processus de « sémiotisation » est de plus en plus un élément intégrateur de la description théorique du monde, et il constitue désormais un élément essentiel de la construction conceptuelle des sciences physiques et mathématiques.

Limitons-nous à citer les deux autres exemples. (i) La force et l’importance des images en topologie pour permettre d’explorer et de mieux appréhender les transformations des formes possibles des objets et leurs relations réciproques, notamment la relation d’équivalence qui permet de définir de façon naturelle la notion importante de type (invariant) topologique. Le principal intérêt de cette notion vient de ce qu’elle permet une caractérisation morphologique des propriétés actuelles et potentielles des espaces. (ii) La qualité sensible couleur, dont on essayera de mettre en évidence son organisation en plusieurs niveaux de constitution et ses différents statuts de représentation, et à laquelle, ensuite, on associera une gerbe de significations qui se déploient et varient en fonction du plexus perceptif et/ou sémiotique. À partir de cet exemple, c’est un point général qui nous importe de souligner, à savoir le caractère dynamique de l’émergence des qualités sensibles, la multiplication de leurs effets morphologiques prégnants et les changements de signification qui peuvent en résulter.

3. Le rôle et la force de l’image dans la visualisation topologique

Le deuxième exemple est pris de la discipline mathématique qui est le domaine par excellence des images (des figures, des dessins) au sens nouveau et particulier que nous venons de préciser, à savoir la topologie. C’est la partie la plus abstraite (mais, dans un autre sens, la plus concrète) des mathématiques, qui se définit comme cette science des transformations d’objets étendus et d’espaces plus ou moins abstraits par déformations continues, c’est-à-dire sans coupures ni déchirures. Dans ce domaine des mathématiques, les notions de distance et de longueur ne jouent plus aucun rôle, et le concept de congruence (de coïncidence par superposition) se révèle impuissante à rendre compte de la similitude et des relations intrinsèques entre deux objets, deux figures, deux surfaces, ou, plus généralement, entre deux espaces abstraits. Le critère de similitude par superposition ou par reproduction des grandeurs, et donc la notion même de ressemblance visible, perd tout son sens en topologie. Dans aucun autre domaine des mathématiques, l’éloignement de la réalité visible et du modèle de la figuration est aussi important comme ce l’est en topologie, où un concept beaucoup plus subtil et proche de la structure intrinsèque des objets joue un rôle fondamental, il s’agit du concept qualitatif (au sens topologique, c’est-à-dire où n’interviennent pas de relations métriques) d’équivalence ou d’homéomorphisme.

Rappelons que la topologie est cette branche des mathématiques où la géométrie est souple : deux configurations deviennent équivalentes dès qu’elles ont « la même forme ». Il n’y a par exemple aucune différence de nature topologique entre une tâche d’encre et un disque, entre un carré et un cercle, ou encore entre une sphère et un ellipsoïde. Cette propriété d’avoir la même forme s’exprime rigoureusement en mathématique par la notion d’homéomorphisme. De manière plus générale, l’objet de la topologie est précisément de mettre en évidence des invariants qui rendent compte de certaines propriétés des objets qu’elle étudie. Parmi les premiers invariants mis à jour, citons la célèbre caractéristique d’Euler-Poincaré, découvert par Euler en 1752 : dans un polygone convexe (un polyèdre est convexe si toutes ses diagonales sont contenues dans son intérieur), le nombre de ses faces et sommets, diminué du nombre de ses arêtes, vaut toujours 2. Plus récemment, un autre exemple particulièrement important est la découverte en 1983 de nouveaux invariants de nœuds : les polynômes de Jones, qui permettent, entre autres, de distinguer certains types de nœuds de leurs images dans un miroir. Toutefois, certains nœuds admettant des polynômes de Jones identiques, la recherche d’invariants à même de distinguer tous les nœuds demeure largement ouverte, preuve que la topologie recèle encore de nombreux mystères.

Les objets de la topologie, nommées variétés topologiques, forment un zoo difficilement concevable tant il est riche. Ici, les notions d’homéomorphisme (équivalence topologique entre deux variétés), de bord (ou frontière) et d’orientabilité (ou non-orientabilité) sont d’une importance capitale, car elles permettent de caractériser les propriétés globales des espaces. Pour les surfaces (variétés de dimension 2), par exemple, un rectangle (plein) est homéomorphe à un cylindre — pour réaliser l’homéomorphime, il suffit d’appliquer le principe de recollement ou la notion identique d’ensemble quotient. On peut aussi courber d’un demi-tour le rectangle (pourvu qu’il soit assez long), et on obtient alors le célèbre ruban de Möbius. C’est l’exemple le plus simple de surface non-orientable : le ruban de Möbius n’admet en effet qu’une seule face. Toujours en appliquant la technique du recollement, on peut superposer les bords (les deux cercles) d’un cylindre, et l’on obtient ainsi un tore. Tout comme la sphère, le tore est une variété sans bord et orientable, mais, du fait du trou qu’il présente en son milieu, il n’est pas homéomorphe à la sphère, c’est-à-dire que les deux variétés bidimensionnelles ne peuvent pas être déformées continument l’une dans l’autre. Coller les bords d’un cylindre avec des orientations opposées, c’est une opération qui peut se faire uniquement dans l’espace à quatre dimensions, alors que les transformations citées jusqu’à maintenant peuvent être réalisées dans notre espace à trois dimensions. La raison pour laquelle il faut ajouter une quatrième dimension, réside en ce que l’opération nécessite en effet de passer par l’intérieur du cylindre, d’où un croisement problématique dans notre espace à trois dimensions. L’objet obtenu s’appelle une bouteille de Klein. Cet objet « vit » dans un espace a quatre dimensions, et il constitue le premier exemple de variété à la fois sans bord et non-orientable : contrairement à la sphère ou au tore, elle n’a ni intérieur, ni extérieur !

Pourquoi ne peut-on déformer, sans le déchirer, une sphère en un tore ? Comment décrire, et surtout caractériser les différentes variétés ? La réponse à ces questions est contenue pour l’essentiel dans les travaux de Poincaré à la fin du XIXe siècle sur l’Analysis Situs, qui marquent la naissance de la topologie algébrique moderne. Poincaré y expose l’idée géniale d’associer aux variétés des invariants qui ne sont plus des nombres, mais des structures algébriques complètes ! Ces structures sont des « groupes ». L’étude de ces groupes constitue l’objet d’étude de la topologie algébrique (et sous une forme plus élaborée, de l’algèbre homologique). Les découvertes de Poincaré s’articulent autour de deux grandes idées : d’une part, il est possible d’associer à une variété ses « groupes d’homologie », d’où une nouvelle interprétation de la caractéristique d’Euler-Poincaré et des nombres de Betti (comme dimensions des groupes d’homologie) ; d’autre part, de nombreuses informations relativement à une variété peuvent être codées dans un objet appelé « groupe fondamental » (ou « groupe de Poincaré »). Les deux notions ne sont pas complètement étrangères puisque le premier groupe d’homologie se déduit aisément du groupe fondamental, en des termes plus précis, le premier groupe d’homologie est l’abélianisé du groupe fondamental, c’est-à-dire le quotient du groupe fondamental par son commutateur. Pour expliquer de manière intuitive cette notion fondamentale introduite par Poincaré, on a besoin maintenant plus d’élastiques que de colle ! Plus exactement, l’objet mathématique qui nous intéresse porte le nom de « lacet » et, à quelques subtilités près, c’est simplement une courbe fermée dessinée sur une variété.

Comme d’habitude en topologie, nous pouvons manipuler librement ces élastiques (sans toutefois les rompre) et lorsque l’on peut passer d’un lacet à l’autre par une déformation continue, on dit d’eux qu’ils sont « homotopes ». Sur le plan et la sphère, il n’est pas difficile de se convaincre que deux lactés sont toujours homotopes ; en d’autres termes, ces surfaces jouissent de la propriété de la « simple connexité ». (Cette propriété joue un rôle essentiel dans la formulation de la conjecture de Poincaré). La situation est cependant différente pour la plupart des autres variétés ! Par exemple, les lacets sur un cylindre se scindent en deux catégories : ceux qui sont enroulés autour du cylindre et les autres. Il est en effet impossible de déformer continument et en restant sur la surface du cylindre les lacets de la première catégorie pour obtenir ceux de la seconde catégorie. De même on peut identifier trois catégories de lacets pour le tore. L’objet du groupe fondamental est précisément de classer les lacets d’une variété selon qu’ils sont homotopes ou non (en incorporant au passage des informations supplémentaires, comme le « nombre d’enroulements »). La complexité d’une variété se reflète ainsi sur son groupe fondamental, et certaines opérations (comme les recollements) se traduisent par des « calculs » sur les groupes fondamentaux. Une variété dont le groupe fondamental est le plus simple possible, tels le plan ou la sphère, est dite « simplement connexe ». A l’opposé, le tore, le cylindre, le ruban de Möbius et bien d’autres variétés ne sont pas simplement connexes. Parmi toutes les surfaces, la sphère occupe ainsi une position singulière, car c’est la seule à être à la fois sans bord, « compacte » (ce qui signifie grosso modo qu’elle est bornée dans l’espace, contrairement au plan) et simplement connexe. Guidé par son intuition géniale, Poincaré a deviné que ces propriétés (absence de bord, compacité et simple connexité) caractérisaient non seulement la sphère usuelle mais aussi les sphères de dimension supérieure. Les cercles et les sphères ont en effet des grandes sœurs dans les espaces à quatre dimensions et plus. Ses résultats et ses intuitions l’ont ainsi conduit à énoncer sa conjecture : toute variété compacte de dimension n = 3 (ou plus), sans bord et simplement connexe, est homéomorphe à une sphère de dimension n.

La représentation en topologie ne peut se passer d’un processus de « visualisation mathématique » (d’idéalisation ou d’imagination). Cette visualisation fait appel à un nouveau type d’intuition, plus conceptuelle et en même temps plus picturale (diagrammatique), et résolument éloignée des sensations immédiates et de l’intuition empirique. En topologie, la figure, le dessin, le diagramme ou le graphe (dans ce contexte, nous attribuons à ces mots le même statut) ne sont plus l’image de quelque chose, d’un objet extérieur que l’image se chargerait de représenter, mais sont eux-mêmes l’objet qui représente un univers de relations et de propriétés « cachées » absentes de l’image. On peut ainsi dire qu’en topologie, la « sémiotisation » du statut de l’image est encore plus développée par rapport à d’autres sciences et elle a atteint un niveau très fin. La topologie permet une autre approche dans l’étude des objets qui ne se retreint pas aux relations quantitatives de grandeur et aux aspects visuels, mais considère davantage la forme (l’« image ») dans sa globalité, ainsi que le spectre des variations possibles (continues ou discrètes) de ses configurations. Bref, la topologie a changé en profondeur notre pensée et culture scientifiques de l’image.

La pensée topologique concerne de près l’apparent dualisme entre modèles continus et modèles discontinus. Il est permis de penser qu’il est possible d’élaborer une théorie mathématique « idéale » capable de traiter, de façon cohérente, des situations et des systèmes qui évoluent en général de façon continue, tout en admettant des sauts discrets. Il semble d’ailleurs que, dans la nature, se produisent les deux types de changements comme s’ils découlaient d’un processus unique.

On peut illustrer ce qui vient d’être dit par l’exemple suivant : on sait qu’une séquence appropriée de changements de pression et de température peut faire passer continûment l’eau (ou tout autre liquide) à l’état de vapeur, sans qu’il y ait réellement ébullition. L’un des états a assumé l’identité de l’autre par une transformation continue. Mais on sait par ailleurs que l’ébullition de l’eau est ce qu’on appelle (dans le langage des catastrophes de René Thom) « une catastrophe de type fronce ». Si la vapeur absorbe le liquide, c’est que l’eau entre brusquement en ébullition mais, pour que cela arrive, il faut changer la valeur d’une des « variables d’état » (en l’occurrence ce sera la température) ou bien la « variable dynamique » temps. En fait, de nombreux types de conflit entre deux états physiques interviennent lorsqu’on introduit du discret dans une situation continue.

La question des rapports entre modèles continus et modèles discrets doit pouvoir se ramener, en principe, à un problème de topologie. Il s’agit à ce moment-là : (i) de déterminer si deux variétés sont ou non topologiquement équivalentes ; (ii) d’établir une classification de toutes les variétés possibles ; (iii) de trouver toutes les façons de plonger une variété dans une autre (comme, par exemple, un cercle noué dans l’espace à trois dimensions) ; (iv) de déterminer si de telles insertions sont ou non les mêmes. Depuis que Poincaré a conjecturé en 1905 que « la seule variété à trois dimensions fermée et simplement connexe est la sphère (topologique) S³ », beaucoup de résultats ont été obtenus. Aux environs de 1930, Henry Whitehead découvre à l’aide de la théorie homotopique comment l’énoncé de Poincaré peut se généraliser en dimension quelconque. Autrement dit, il découvre comment on peut donner à toute variété lisse une structure linéaire par morceaux, ou, selon la belle image du mathématicien Ian Stewart, « comment on peut déformer un œuf pour lui donner la forme d’une part de fromage ». Dans les années 1950, on a montré que toute variété topologique à trois dimensions a une structure lisse unique, c’est-à-dire (pour utiliser encore une image parlante) qu’un morceau de pâte irrégulier peut être transformé pour prendre l’aspect d’un œuf. Dans ce cas, l’œuf peut avoir des poignées, des trous ou des boutons : ce qui compte, c’est uniquement l’état de la surface.

Les sphères d’homotopie∑ⁿ, introduites par Whitehead, sont les variétés fermées ayant la propriété que, si on leur enlève un point, ce qui en reste peut être déformé continument en lui-même jusqu’à ce qu’il devienne un autre point. La conjecture de Poincaré généralisée dit qu’il n’y d’autre ∑ⁿ que Sⁿ lui-même, autrement dit, une variété à n dimensions qui possède les mêmes groupes d’homotopie que la sphère à n dimensions. ∑ⁿ est topologiquement équivalent à la sphère Sⁿ. On vérifie facilement que ceci est vari pour n = 1 ou 2 ; pour n = 5, le résultat a été prouvé par Steven Smale en 1956, et pour n = 4 par Michael Freedman en 1982. On connaît aujourd’hui, grâce aux résultats obtenus en 2003 par le mathématicien russe Grigori Perelman, la réponse complète pour n = 3, qui était le cas initialement considéré par Poincaré.

Si on a à l’esprit le point fondamental qu’un espace où la courbure sectionnelle est constante, c’est-à-dire K = –1, 0 ou 1 si on normalise est localement isométrique à l’espace hyperbolique, à l’espace euclidien ou à la sphère ronde (si de plus l’espace est supposé simplement connexe, on a une isométrie globale), on peut alors reformuler la conjecture de Poincaré comme un problème géométrique :

Un point culminant de son travail est le théorème des voisinages canoniques qui décrit la géométrie des flots de Ricci de dimension 3 aux points de grande courbure scalaire. Cette connaissance précise de la géométrie aux points de grande courbure permet de faire des chirurgies de manière contrôlée. Perelman démontre qu’on peut poursuivre ce flot avec chirurgie indéfiniment, et ce pour toute donnée initiale normalisée sur une variété compacte de dimension 3. Un argument simple de diminution du volume montre qu’il n’y qu’un nombre fini de chirurgies sur chaque intervalle de temps fini. Par contre, elles peuvent se poursuivre pendant un temps infini. La variété peut devenir non connexe et certaines composantes peuvent disparaître lors des chirurgies, on dit qu’elles s’éteignent. Le point clé est que grâce au théorème des voisinages canoniques la topologie de ces composantes est connue. Il s’agit des quotients de la sphère S³, des produits S²xS¹, d’espaces projectifs RP³ ou des sommes connexes d’espaces projectifs. Il peut même arriver que toutes les composantes de la variété s’éteignent en temps fini. Si la variété de départ est simplement connexe, on sait alors qu’il n’y a que des sphères et que la variété initiale est difféomorphe à la sphère S³.

C’est la stratégie développée par Perelman, où l’extinction du flot avec chirurgie en temps infini est prouvée grâce à l’annulation d’un invariant géométrique ad hoc. Une version de cette méthode, techniquement plus simple, permet de montrer que la largeur de la variété, une quantité géométrique calculée à l’aide d’un balayage par des sphères S², décroît jusqu’à zéro en temps fini le long d’un flot de Ricci lisse. On peut en déduire l’extinction en temps fini pour le flot avec chirurgie. La situation contraire est aussi considérée, l’évolution du flot avec chirurgie en temps infini et la géométrisation de la variété. En d’autres termes, Perelman prouva que, lorsque le flot s’écoulait, les points où survenaient des singularités donnaient des régions que l’on pouvait découper de la variété d’origine et qui présentaient des géométries homogènes au sens de Thurston. Après avoir coupé ces morceaux, on pouvait relancer le flot de Ricci et le laisser s’écouler jusqu’à ce que se forment de nouvelles régions à géométries homogènes. On pouvait à nouveau découper ces régions et relancer le flot.

On ne pouvait imaginer interaction plus fine entre géométrie et topologie. C’était presque comme si la conjecture de géométrisation de Thurston et le flot de Ricci avaient été conçus ensemble. Le flot de Ricci est un outil puissant qui façonne la variété l’étirant et la déformant, y découpant des morceaux à géométries homogènes. À la fin du processus, l’intégralité de la variété est décomposée en morceaux géométriques. On peut dire que la 3-variété est effectivement portionnée par le flot de Ricci en des sous-variétés ou, par analogie avec un organisme vivant, en des « variétés-filles ». Le résultat final est particulièrement signifiant. Considérons une variété de dimension 3 fermée et finie. On peut utiliser des méthodes standard de topologie différentielle pour la munir d’une structure géométrique. Considérons maintenant le flot de Ricci et laissons la variété évoluer en conséquence. Si la variété est simplement connexe, alors Perelman montre que le flot de Ricci, éventuellement après quelques chirurgies bénignes, finira par lisser les extrema de courbure, donnant au final une variété de courbure positive constante, homéomorphe à la variété de départ. Il est alors possible de montrer qu’une 3-variété simplement connexe et de courbure positive constante est nécessairement une sphère tridimensionnelle, ce qui résout donc la conjecture de Poincaré.

Une variété topologique est un objet très flexible, qu’on peut tordre et replier à volonté. La géométrie classique, euclidienne et non euclidienne, s’intéresse à des objets beaucoup plus rigides, mais dont la structure est en même temps mathématiquement plus facile à traiter. Il y a une métrique, c’est-à-dire des distances qui se prêtent difficilement à être modifiées. L’espace n’est pas extensible. Il y a trois géométries fondamentales, chacune applicable à une surface à courbure constante, et chaque type de surface topologique est associée à l’une de ces géométries, et peut être construit à partir d’elle. Plus précisément, on peut attribuer à chaque surface une métrique de courbure constante, soit nulle, soit négative, soit positive. Le choix ne dépend que d’un invariant topologique : le nombre (entier) d’Euler ꭓ, appelé aussi caractéristique d’Euler-Poincaré.

Mais, du moment qu’on essaye de généraliser cette relation entre géométrie et topologie en trois dimensions et plus, plusieurs difficultés apparaissent. D’abord, les variétés à trois dimensions sont beaucoup plus compliquées que les surfaces. L’une des complications vient de ce que, au lieu des trois géométries possibles en deux dimensions, il y en a huit possibles en trois dimensions. En réalité, il faudrait parler d’au moins trois types de variétés : linéaires par morceaux (dans ce cas toute ligne droite d’un morceau doit se raccorder à une ligne droite de l’autre), topologiques (ce sont les variétés qui peuvent subir toutes sortes de déformations, pourvu que la notion de continuité soit préservée), lisses ou différentiables (les courbes régulières de l’un des morceaux doivent correspondre à des courbes régulières de l’autre). Or, il peut arriver qu’un théorème soit vrai pour les variétés de type linéaire par morceaux, mais pas pour les variétés lisses. C’est là une situation tout à fait remarquable, et une nouvelle complication s’ajoute alors aux précédentes. En effet, en 1963, John Milnor a découvert l’existence de plusieurs structures lisses (28 exactement !) sur la sphère à sept dimensions. En 1983, le mathématicien britannique S. Donaldson découvre que R⁴ possède une infinité de structures différentiables dites « exotiques » ! Il reste deux questions fondamentales : d’abord, à quoi peuvent bien ressembler ces structures lisses exotiques de l’espace à quatre dimensions ? ensuite, dans quelles situations et sous quelles conditions est-il possible de passer de l’une à l’autre de ces trois types de variétés, ou quelles sont les formes possibles d’intersections entre le contextes topologique, différentiable et linéaire par morceaux ?

4. Les ordres de la couleur et ses fonctions de représentation dans la perception

Le troisième et dernier exemple concerne le statut de la couleur et sa fonction de représentation. Déjà Hering avait remarqué qu’il faut caractériser la couleur, si l’on en fait une analyse phénoménologique, moins sur des états subjectifs que sur des structures d’objets, plus comme une propriété que comme une sensation. Il ne s’agit pas, avec la vue, d’une intuition des rayons en tant que tels, mais de l’intuition des choses extérieures par l’entremise des rayons : l’œil n’a pas à nous instruire sur l’intensité ou la quiddité de la lumière qui nous vient des choses, mais sur ces choses mêmes. Il apparaît donc nécessaire, même du point de vue de l’optique physiologique, de distinguer ce type de « vue » qui se réduit à une réceptivité aux impressions lumineuses et à leurs différences et ce type de « vision » dans lequel le monde intuitif se constituer pour nous. C’est ce qu’enseigne notamment la constance des choses vues.

Remarquons que, d’une part, la même « sensation de lumière » peut revêtir des significations objectives très différentes selon le contexte relatif aux modes de transmission et de diffusion de la lumière dans tel et tel milieu pouvant affecter, selon des modalités variées, notre perception des objets qu’y sont situés. Comme conséquence, on aura notamment que l’image et son contenu variera en fonction des changements à la fois du « milieu lumineux » et des modes de sa configuration et distribution dans l’espace ambiant. De l’autre, il est possible de montrer que plusieurs ordres se différencient dans le phénomène que nous nommons « couleur » et que selon l’appartenance à tel et tel de ces ordres le phénomène lui-même change entièrement pour nous de valeur, de signification. Dans le premier, on prend la couleur pour une « image lumineuse », saisie comme telle et interprétée selon sa détermination propre, sans que lui incombe la fonction de faire voir et de représenter un être objectif. Dans le second, le regard se tourne à l’inverse vers de pures déterminations objectives, et la couleur n’est jamais traitée que comme une trace (ou une empreinte) de l’être objectif qui apparaît en elle, sans qu’il soit nécessaire qu’on la considère selon son propre mode phénoménal.

De ce point de vue, la perception des choses et la perception des images lumineuses semblent peu compatibles ; la perception de la chose veut que les images lumineuses se retirent graduellement à l’arrière-plan où elles sont indispensables, pour que les « vraies » formes des choses émergent nettement à partir de cette contamination de plus en plus saillante du support ou du milieu spatial par la lumière. Au cours de ce processus, la lumière et avec elle l’image lumineuse se retirent au fond de la scène visuelle, et en même temps les contours des choses se précisent et s’organisent de telle sorte à permettre la formation de ce que nous appelons « figures ». Les figures (ou les gestalts) et par leur entremise les choses (les objets), sont donc à distinguer des images lumineuses. Si ces dernières se trouvent à l’endroit (au sens de « lieu topologique ») convenable et si elles se distribuent de manière appropriée, la perception de la chose a lieu. En revanche, là où les images lumineuses s’accentuent et envahissent la scène (le champ visuel) au point qu’on ne puisse plus les négliger, la perception et avec elle la possibilité même de re-connaître les choses et le monde qu’elles habitent, se trouble et se réduit.

On voit ainsi, par ces brèves considérations, qu’il y a un lien causal très précis entre l’ordre selon lequel une « couleur » entre en relation avec le sujet (avec notre perception consciente) et l’objet représenté par cet ordre : le changement de l’ordre des couleurs a pour conséquence immédiate le changement de l’objet représenté. Ce qu’on nomme ici ordre des couleurs, c’est très précisément cette « vue » produite par la fonction de représentation particulière que remplit la couleur dans chaque cas singulier. La simple couleur est ce qui nous représente les choses. Mais il ne suffit pas que la couleur soit là pour représenter des choses ; il faut en outre qu’elle s’organise, s’ordonne et pénètre dans des formes. Espace et forme nous sont représentés par l’entremise de cet ordre des couleurs. Par rapport à la couleur, l’espace est donc quelque chose de représenté. La couleur même n’est pas représentée ; directement donnée, elle représente des formes dans l’espace. La forme, elle, représente la chose avec ses propriétés. La forme est cependant plus qu’un attribut ou une qualité de la chose, elle est un « objet » représenté qui à son tour a un pouvoir de représenter un monde d’objets, de phénomènes et d’événements autre que la chose accessible directement par l’image.

5. Nœuds, diagrammes des nœuds et formation de l’espace

L’information sur les « nœuds-surfaces » (c’est-à-dire les nœuds qui admettent une projection plane) dans l’espace tridimensionnel conçu mathématiquement, résulte d’une structure appelée diagramme du nœud. Pour l’étude mathématique des nœuds, la question fondamentale que l’on va se poser et à laquelle on essayera de répondre est de savoir si deux nœuds sont-ils équivalents ? Si deux nœuds ne sont pas équivalents, on peut alors les distinguer, généralement au moyen d’invariants topologiques ou algébriques : l’un de ces invariants est le groupe du nœud. La plupart de ces invariants peuvent s’obtenir à partir de diagrammes de nœuds. D’ailleurs, si au moins deux nœuds sont équivalents, c’est que nous pouvons alors définir une isotopie qui nous montre l’existence d’une telle équivalence. Le concept topologique d’isotopie permet de définir une relation d’équivalence entre des variétés ou des sous-ensembles de Rⁿ.

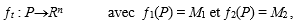
où t∈ I, I est l’intervalle unité défini dans R (le corps des réels). On appelle cette application une isotopie de P.

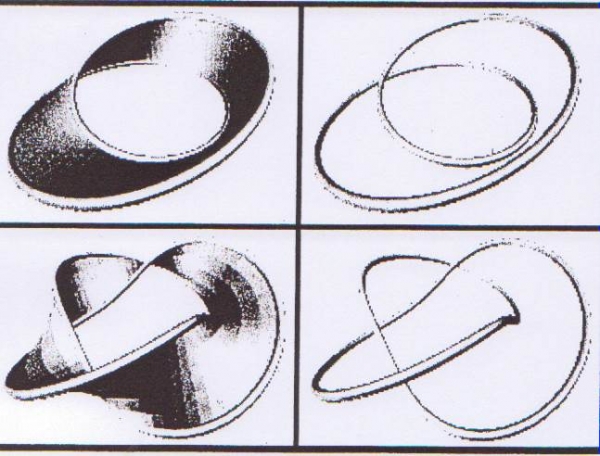
Il s’ensuit que deux variétés (ou sous-ensembles) de Rⁿ seront dits équivalentes s’il existe une isotopie entre elles. Considérons, par exemple, un ruban de Möbius dans R³, M₁. Prenons ensuite un exemple similaire et considérons un « ruban circulaire avec trois demi-torsions », M₂. Il est facile de montrer que M₁ et M₂ ne sont pas deux variétés (ou sous-ensembles) isotopes. L’idée de la démonstration consiste à supposer que si elles étaient isotopes, alors les espaces (ensembles) à bord correspondants seraient équivalents : des cercles S¹ dans R³ dans un cas, et des sphères bidimensionnelles S² dans R⁴ dans l’autre. Mais ce n’est pas le cas, puisque le bord de M₁ est un nœud trivial (un cercle), tandis que le bord de M₂ est un nœud non trivial, plus précisément un nœud de trèfle (la courbe nouée la plus simple dans S³ ou R³), formé de trois croisements et pour dénouer lequel il suffit une seule manipulation. Il importe d’ores et déjà de noter qu’il peut y avoir plusieurs diagrammes (ou projections planaires) d’un même nœud. Nous voudrions souligner en particulier que, dans de nombreuses situations, on peut se représenter le même objet de manières différentes, et cela dépend à la fois de la dimension de l’espace considéré et de la nature de la représentation choisie.

Fig. 1 Différentes représentations du ruban de Möbius.

On obtient un ruban de Möbius en faisant tourner régulièrement un segment de longueur constante autour d’un cercle avec une rotation d’un demi-tour, ou plus généralement, d’un nombre impair de demi-tours ; ces divers rubans sont homéomorphes, mais non-isotopes dans R³ (on ne peut passer continûment de l’un à l’autre), et pour chaque nombre de demi-tours, il existe deux classes d’isotopies, images-miroir l’une de l’autre. De plus, le ruban à trois demi-tours a pour bord un nœud de trèfle, et plus généralement, le ruban à 2p + 1 demi-tours a pour bord un nœud torique d’ordre (2p + 1, 2).

Une petite parenthèse est peut-être ici nécessaire pour expliciter le sens de quelques notions que nous venons juste d’utiliser. Je rappelle que l’image la plus familière du ruban de Möbius est une « bande circulaire qui présente une demi-torsion (un tour de 180° autour d’un axe) », appelée aussi « contorsion » (writhe) ; le tirebouchon et le tournevis en sont des exemples très significatifs. Plus précisément, il s’agit de l’image d’un plongement d’une variété de dimension 2, S², dans l’espace « ambiant »R³. Citons enfin la propriété contre-intuitive que cette variété n’est pas orientable (voir les figures 2(a) et 2(b)), ce qui veut dire, en des termes plus techniques, qu’il n’est pas possible d’y définir le groupe d’homotopie trivial π₁(M²). Les variétés qui admettent un tel groupe sont celles qui peuvent être déformées en un point. La propriété d’orientabilité est de nature globale et elle permet la mise en évidence de plusieurs caractéristiques très subtiles des espaces, que nous n’aborderont pas ici (le lecteur intéressé pourra se référer à notre travail (Boi, 2006)).

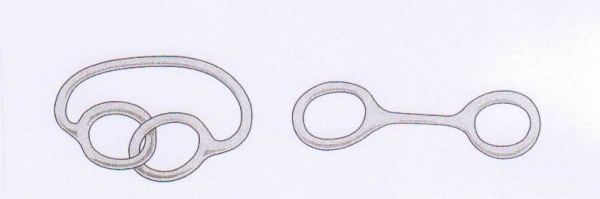
Fig. 2(a). Le cylindre et le ruban de Möbius ne sont pas isotopes. Le premier est orientable, le second ne l’est pas.

Fig. 2(b). Deux objets étonnement isotopes. Les deux sont orientables.

Définition. Soient V et W deux variétés de classe C^k (éventuellement k infini), et ƒ une application de V dans W. On dit que ƒ est un C^k-plongement si pour tout x appartenant à V, le rang de l’application linéaire tangente Tƒ(x) est égal à la dimension de V (elle est donc injective), et si en outre ƒ est un homéomorphisme de V sur ƒ(V).

En topologie, un homéomorphisme est un isomorphisme entre deux espaces topologiques, c’est une bijection continue de l’un sur l’autre, dont la réciproque est continue. La notion d’homéomorphisme est la bonne notion pour dire que deux espaces (ou, d’une manière plus intuitive, deux objets élastiques, donc déformables) sont le « même » mais vus différemment. Philosophiquement, cela signifie qu’on peut envisager pour tout espace un processus morphodynamique qui nous permet d’avoir une « vision interne » des transformations dont il est susceptible. Exemples : une sphère est homéomorphe à un cube, et une tasse (un objet à une anse) est homéomorphe à une chambre à air (un objet à un trou). C’est la raison pour laquelle les homéomorphismes sont les isomorphismes de la catégorie des espaces topologiques.

Définition. Soient V et W deux variétés de classe C^k (éventuellement k infini), et ƒ une application de V dans W. On dit que ƒ est une C^k-immersion si pour tout x appartenant à V, le rang de l’application linéaire tangente Tƒ(x) est égal à la dimension de V (elle est donc injective).

En modifiant légèrement la notation, on peut aussi dire qu’une immersion de X dans Y, où X et Y sont deux espaces topologiques, est une fonction lisse, ƒ, qui envoie X dans Y, et dont la propriété fondamentale est d’être localement bijective mais pas globalement. De façon analogue, on peut définir une immersion comme une application lisse dont le différentiel, dƒ, est non singulier.

On a ainsi la proposition intéressante qu’une variété immergée est l’image d’une immersion. Par exemple, le limaçon dont le graphe de la fonction en coordonnées polaires s’écrit : r = ½ + cosθ, est un cercle immergé dans le plan.

Le rôle que les concepts de plongement et d’immersion ont dans toute théorie morphologique de l’espace, et dans toute tentative de comprendre la signification des transformations auxquelles ces concepts peuvent donner lieu ne saurait en aucun cas être sous-estimé. Ils sont particulièrement importants pour comprendre les possibilités et les limites des relations que les objets-surfaces de notre univers mathématique peuvent avoir avec l’espace ambiant.

La surface de Boy est le nom donné au plan projectif réel RP², muni de sa topologie quotient, car elle se définit comme le quotient de R³\{0} par la relation d’équivalence suivante : « deux vecteurs non nuls sont équivalents si et seulement s’ils sont colinéaires ». La surface de Boy peut aussi être « vue » comme une sphère dont on a recollé deux à deux les points antipodaux, ou encore un disque dont on a recollé deux à deux les points diamétralement opposés de son bord. On peut également la construire en recollant le bord d’un disque sur le bord d’un ruban de Möbius. Des nombreuses images correspondant à des étapes de la formation de la surface de Boy peuvent être obtenues en faisant croître un ruban de Möbius à trois demi-tours pour le transformer en surface de Boy, son bord circulaire convergeant vers un point.

La bouteille de Klein est une surface fermée, sans bord et non orientable, c’est-à-dire une surface pour laquelle il n’est pas possible de définir un « intérieur » et un « extérieur ». Elle est impossible à réaliser dans l’espace à trois dimensions, car il faut alors qu’elle se traverse elle-même ; aussi, aucune réalisation que l’on peut voir de la bouteille de Klein n’est exacte. Dans R⁴, il est par contre possible de la réaliser sans auto-intersection. Il est possible de comprendre la structure de la bouteille de Klein en essayant de la « visualiser » dans un espace à 4 dimensions ; il suffit de s’imaginer qu’à l’endroit où la surface s’auto-intersecte, en réalité, la bouteille passe « dessus » et « dessous » au sens de cette quatrième dimension, et donc ne s’auto-intersecte pas. On peut en quelque sorte considérer que la bouteille de Klein est une surface qui fait un « nœud ». En tant que surface (objet à 2 dimensions), il lui faut 4 dimensions pour faire un nœud, de même que pour une courbe (objet à une dimension) il faut 3 dimensions pour faire un nœud.

On peut toujours transformer un plongement en une immersion. Prenons une sphère et amenons au contact, à l’intérieur, deux points par exemples antipodaux (des « pôles »). Dans cet univers « immatériel » des immersions, les surfaces peuvent s’auto-traverser. Il y a alors création d’une courbe d’auto-intersection (par exemple, un cercle).

Mais l’inverse n’est pas automatiquement possible. Ainsi le plan projectif ne peut être plongé dans R³, il ne peut y être qu’immergé. La forme classique de cette immersion est la surface de Boy, qui possède un ensemble d’auto-intersection en forme d’hélice tripale, avec un point triple, où se croisent trois nappes. Même chose pour la bouteille de Klein, dont l’auto-intersection minimale est une courbe fermée. Les plongements peuvent être considérés comme des cas particuliers d’immersions, où l’ensemble d’auto-intersection est vide.

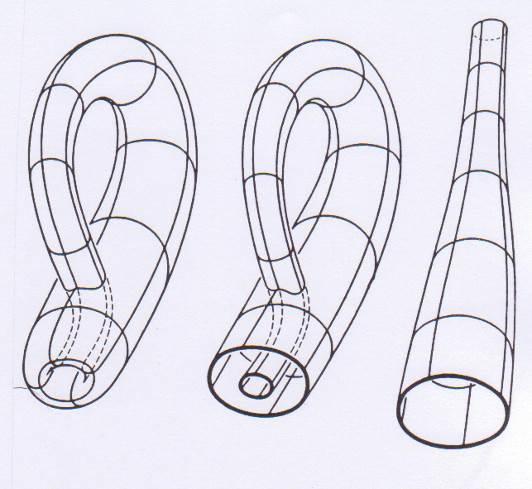
Fig. 3. La bouteille de Klein et les dimensions de l’espace.

La bouteille de Klein est une surface fermée, sans bord et non orientable, c’est-à-dire une surface pour laquelle on ne peut pas définir un « intérieur » et un « extérieur ». Elle est un exemple d’une extension du ruban de Möbius (une surface unilatère, qui n’a ni devant ni derrière) dans la quatrième dimension. La bouteille de Klein n’admet pas d’immersion dans l’espace à trois dimensions. En d’autres termes, elle n’est pas réalisable dans l’espace tridimensionnel R³, car il faut alors qu’elle se traverse elle-même ; aussi, aucune réalisation que l’on peut voir de la bouteille de Klein n’est exacte. Dans R⁴, il est par contre possible de la réaliser sans auto-intersection. Topologiquement, la bouteille de Klein est la somme connexe de deux espaces projectifs réels ; sa caractéristique d’Euler-Poincaré est nulle ; et ses nombres de Betti non nuls sont b₀ = 1 et b₁ = 1.

Rappelons que le plan projectif n’admet pas d’immersion dans l’espace à trois dimensions R³. En revanche, on sait maintenant (grâce à la découverte faite en 1901 par le mathématicien allemand et élève de Hilbert Werner Boy) que la surface de Boy réalise une immersion du plan projectif réel dans R³. Il est possible de construire cette surface de l’intérieur, ce qui permet de mieux en mettre en évidence ses propriétés topologiques. Le procédé consiste à se donner un point triple où s’intersectent trois plans définis par des systèmes de coordonnées planaires dans R³. En fait, le nombre des points triples d’une surface S immergée dans R³ doit être congruent, modulo 2, au carré de la première classe de Stiefel-Whitney de S dans H²(S ; Z/2). L’exécution complète de cette construction permet d’obtenir la surface de Boy comme une immersion du plan projectif. Il s’agit d’une immersion linéaire par morceaux, mais ses arêtes et coins peuvent facilement être arrondis (« lissés ») de sorte à obtenir une immersion différentiable (lisse).

On obtient une construction inexacte (c’est-à-dire avec auto-intersection) de la bouteille de Klein dans R³, en prenant un carré initial et en collant les deux bords de la même couleur l’un contre l’autre dans le même sens des flèches. La figure obtenue est un cylindre, dont on veut identifier les deux bords à l’aide des flèches d’une autre couleur. Pour respecter le sens de ces flèches, il est nécessaire d’opérer une auto-intersection. La bouteille de Klein peut aussi être obtenue par recollement de deux anneaux de Möbius le long de leurs bords. Le plan de construction est facile à réaliser. La propriété qui constitue une preuve d’existence de cette construction est qu’une bouteille de Klein coupée en deux dans le sens de la hauteur par rapport à un plan de symétrie fournit bien deux rubans de Möbius. Il est possible de comprendre et de « visualiser » la structure de la bouteille de Klein à partir de la représentation suivante. Imaginons un individu vivant dans un monde plat, à deux dimensions. On essaye alors d’expliquer à l’individu ce qu’est un nœud. Pour cela, on lui dessine un nœud sur le plan : il ne voit qu’une courbe qui s’auto-intersecte. On lui explique alors que ce ne sont pas des points d’intersections qu’il voit, mais que la courbe passe « dessus » et « dessous ». Notre individu est interloqué : vivant dans un monde plat, il ne comprend pas ce qu’est le dessus ni c’est qu’est le dessous. Il lui manque une dimension, la troisième (le haut et le bas) pour pouvoir visualiser le nœud. Nous rencontrons le même problème lorsque nous essayons de visualiser la bouteille de Klein, puisque nous voyons une surface qui s’auto-intersecte. Néanmoins, si nous raisonnons avec une quatrième dimension, il suffit d’imaginer qu’à cet endroit, la bouteille passe « dessus » et « dessous » au sens de cette quatrième dimension, et donc ne s’auto-intersecte pas. On peut en quelque sorte considérer que la bouteille de Klein est une surface qui fait un « nœud ». En tant que surface (objet à 2 dimensions], il lui faut quatre dimensions pour faire un nœud, de même que pour une courbe (objet à une dimension) il faut 3 dimensions pour faire un nœud.

Fig. 4. Visualisation de l’homéomorphisme ou de la construction topologique des espaces.

Il existe différentes méthodes de création de bouteilles de Klein. On désigne par bouteille de Klein, notée K, tout espace topologique homéomorphe à celui obtenu en identifiant dans un carré plein les côtés opposés avec inversion du sens pour l’un des couples. Cela revient donc à identifier les deux bords d’un ruban fermé sans torsion, avec inversion du sens. Nous pouvons réaliser les constructions suivantes : (fig. 4a) on coud 2 côtés opposés dans le même sens : on obtient un ruban simple (ou un cylindre tronqué) ; (fig. 4b) on coud 2 côtés opposés dans le sens contraire : on obtient un ruban de Möbius ; (fig. 4c) on coud les côtés opposés entre eux dans le même sens : on obtient un tore ; (fig. 4d) on coud les côtés opposés, un couple dans le même sens, l’autre en sens contraire : on obtient une bouteille de Klein ; (fig. 4e) on coud les côtés opposés en sens contraires : on obtient un plan projectif. On obtient donc aussi une bouteille de Klein en cousant deux rubans de Möbius bord à bord. Le ruban de Möbius étant un plan projectif troué, la bouteille de Klein est donc aussi la somme connexe de deux plans projectifs réels. Elle ne peut pas être plongée dans R³, mais seulement immergée avec auto-intersection. (Voir la légende de la figure 3 pour plus de détails concernant les propriétés topologiques de la bouteille de Klein). Si la représentation classique ressemble bien à une bouteille, n’importe quelle surface engendrée par le mouvement d’un cercle (de rayon variable ou non) ou même d’une courbe fermée qui revient sur elle-même après rotation d’un demi-tour est une représentation de la bouteille de Klein. C’est dire qu’on peut obtenir plusieurs représentations différentes (ou divers modèles) de la même bouteille de Klein. On peut par exemple coller un demi-tore avec un demi-dôme de Bohème. On peut aussi faire tourner un huit avec un demi-tour : cette représentation permet de bien voir comment la bouteille de Klein est obtenue en cousant bord à bord deux rubans de Möbius. Et la bouteille de Klein étant la somme connexe de deux plans projectifs, on en obtient une autre représentation en accolant deux bonnets croisés ouverts. Dans R⁴, on peut par contre effectuer le mouvement d’un cercle avec retournement sans que la surface obtenue ne présente d’auto-intersection. On peut également construire un modèle polyédrique de la bouteille de Klein. La bouteille de Klein percée (ce qui revient à être une surface unilatère à un bord de genre 2) peut être représentée par le slip de Möbius : on l’obtient en reliant un ruban fermé non torsadé par une bande. De même que le ruban de Möbius peut être généralisé en un ruban à n demi-tours (et l’on obtient topologiquement un ruban de Möbius seulement quand n est impair), la bouteille de Klein peut être généralisée en une bouteille à n retournements, qui n’est topologiquement une bouteille de Klein que lorsque n est impair.

6. Forme et force des diagrammes, de la physique à la sémiotique

Les diagrammes de Feynman sont des représentations symboliques (concepts graphiques) permettant de calculer les interactions électromagnétiques et les interactions faibles. Ces représentations permettent de « visualiser » les interactions entre les particules élémentaires. Ainsi, par exemple : un proton peut se scinder pour former un pion et un neutron qui se réassembleront peu de temps après pour reformer le proton originel. D’une manière générale, les diagrammes de Feynman décrivent les processus qui ont lieu entre les particules subatomiques.

Les diagrammes de Feynman sont ordonnés dans le temps :

1. de gauche à droite, le diagramme représente l’évolution dans le temps, un processus commence à gauche et se termine à droite ;

2. chaque ligne dans le diagramme représente une particule ; les trois types de particules dans la théorie la plus simple, l’électrodynamique quantique, sont l’électron (un fermion, c’est-à-dire une particule de matière), le positron (qui est aussi un fermion) et le photon (un boson, c’est-à-dire une particule messagère ou « virtuelle ») ;

3. le déplacement vers le haut et vers le bas (verticalement) dans un diagramme indique le mouvement de la particule, mais rien ne montre la direction et la vitesse, si ce n’est que schématiquement ;

4. chaque sommet, point où trois lignes se rencontrent, représente une interaction électromagnétique.

Les diagrammes de Feynman représentent les collisions entre les particules. La scène de ces collisions, c’est le monde physique, c’est-à-dire l’image du monde physique subatomique résultant de la projection de ce monde sur une surface bidimensionnelle sur laquelle on a dessiné des événements. Cette scène exige que l’on spécifie où et quand une certaine action, un certain événement a eu lieu. On a aussi besoin de spécifier les quatre directions : dessus-dessous, nord-sud, est-ouest et la direction de l’espace-temps passé-futur : les quatre coordonnées de l’espace R⁴ (qui correspond au modèle d’espace-temps de Minkowski) qui comprend non seulement l’instant présent, mais aussi le passé et le futur. Un point de l’espace-temps correspond à un événement. Le point de départ de Feynman fut précisément de considérer particules, événements et espace-temps. Le plus simple des diagrammes de Feynman décrit le mouvement d’un électron d’un point a à un point b. La ligne avec une flèche désignant l’orientation représente le propagateur de l’électron. Le propagateur du photon est représenté graphiquement par une ligne ondulée ou en pointillés (discontinue).

Les propagateurs ne sont pas de simples dessins, car ils renferment des instructions pour calculer la probabilité qu’une particule quantique initialement située au point a apparaisse successivement au point b. Feynman eut l’idée radicale qu’une particule ne se déplace pas suivant un seul chemin particulier, mais qu’en réalité elle sonde tous les chemins possibles, aussi bien ceux discontinus que ceux rectilignes. Selon la théorie de Feynman, tous ces possibles chemins contribuent à la probabilité que la particule se déplace de a à b. Tout ceci est implicite dans le concept de propagateur. Les propagateurs concernent l’action coordonnée entre électrons et photons. Quand un électron est perturbé dans son mouvement, alors il peut répondre à une telle perturbation en émettant un photon. Ce processus est l’événement fondamental de l’électrodynamique quantique : tout comme la matière entière est constituée de particules, les processus sont tous constitués d’événements élémentaires d’émission et d’absorption.

Le diagramme qui représente l’événement d’émission d’un photon est appelé diagramme de vertex, il rassemble à la lettre Y, à un branchement d’un arbre ou à une bifurcation : l’électron arrive au point de bifurcation (à la fourche) et émet un photon. Philosophiquement, il suggère une ouverture du réel vers plusieurs évolutions possibles ; ainsi, l’unicité se trouve brisée et cède sa place au multiple. Ce point singulier est plus qu’un signe graphique particulier, car il peut être vu comme l’origine d’un événement phénoménologiquement nouveau, et en même temps un lieu où ce qui est représenté acquière une autre signification. On pourrait pousser plus loin cette réflexion en affirmant qu’à tout nouveau point singulier (ou vertex) peut être associée une différente valeur sémantique : l’électron prend l’un des branchements, le photon prend l’autre. Le point (ou le lieu) où les trois lignes se rejoignent (l’événement correspond à l’émission du photon) s’appelle vertex. Dans les diagrammes de vertex, on dessine le passé pointant vers le bas, et le futur vers le haut. Le photon peut être soit émis soit absorbé.

On peut maintenant utiliser des propagateurs et des vertex pour construire des diagrammes et donc des processus plus complexes. À mesure que la pensée diagrammatique devient plus complexe, elle se trouve davantage associée à une combinatoire des mondes possibles, dans laquelle une variété de plus en plus étendue de significations équivalentes peut être mise en relation avec le même phénomène physique ou objet phénoménologique. Certains physiciens et en particulier Feynman en sont ainsi arrivés à penser que toutes les forces de la nature proviennent (non pas ontologiquement mais conceptuellement) de diagrammes d’échanges spécifiques dans lesquels un photon (ou son analogue) est émis par une particule et absorbé par une autre. La force électrique entre électrons, par exemple, s’obtient d’un diagramme de Feynman où un des électrons émet un photon, lequel est ensuite absorbé par un autre électron. En sautant d’un électron à l’autre, le photon produit la force électrique et magnétique entre les deux particules. Rappelons que les électrons ne sont pas les seules particules pouvant émettre des photons : toute particule possède cette propriété, y compris le proton. Cela signifie que les photons peuvent sauter aussi d’un proton à l’autre, ou d’un proton à un électron, et vice-versa. L’échange permanent de photons entre le noyau et les électrons engendre la force qui assure la cohésion de l’atome. Sans ces photons « sauteurs », l’atome se désintègrerait et l’ensemble de la matière cesserait d’exister.

Les diagrammes de Feynman peuvent être très compliqués ; dans ce cas, ils se transforment en des réseaux de vertex et de propagateurs entrelacés ; ces réseaux peuvent représenter des processus impliquant un très grand nombre de particules. C’est ainsi que d’objets simples (comme un seul photon émis par un seul électron) on passe à des objets complexes (plusieurs particules émises et absorbées). On peut ajouter des flèches autant qu’on veut, pour que les lignes continues deviennent des électrons ou des positrons.

Dans l’électrodynamique quantique, on a trois objets et concepts essentiels entre lesquels on peut établir plusieurs types de correspondances : les particules, les équations (et les calculs que l’on peut faire à partir de ces équations), les diagrammes, c’est-à-dire les représentations graphiques des particules et des équations. La correspondance fondamentale et sa principale signification est celle qui va du diagramme vers les équations puis vers les particules. Les équations comportent déjà une interprétation qui exprime certaines propriétés et certains comportements des entités qui sont supposées appartenir en définitive au monde physique. Mais ce sont les diagrammes les objets déterminants, car ils sont les générateurs à la fois de nouvelles opérations symboliques et d’autres systèmes de signification. Dans l’objet diagramme on a des particules dans différents états, des propagateurs et des vertex, dont la dynamique est engendrée par une grammaire (algèbre) et une sémantique (topologie) plastiques. À cette grammaire et sémantique on peut associer des opérations fondamentales ou des opérateurs de pensée, lesquelles modélisent les transformations et les propriétés de processus physiques réels.

Pour conclure cette section, on soulignera les points suivants.

1. Les diagrammes de Feynman ont révolutionné la physique théorique depuis les année quarante du siècle dernier. Ils ont permis de simplifier les calculs de l’électrodynamique quantique.

2. Ces diagrammes constituent de véritables images de ce qui se produit quand les particules élémentaires se déplacent dans l’espace, entrent en collision et interagissent entre elles. Un diagramme de Feynman peut être formé, soit de quelques lignes seulement pour décrire l’interaction d’une paire d’électrons, soit d’un très grand réseau de trajectoires ramifiées et nouées pour décrire l’ensemble des particules dont est constitué n’importe quel objet, du cristal d’un diamant jusqu’à un être vivant ou à un corps céleste.

3. Ces diagrammes se composent de quelques éléments de base impliquant tout ce qui peut être dit sur les particules élémentaires. D’un point de vue diagrammatique, il n’est pas injustifié d’affirmer qu’« un dessin vaut plus que mille équations ».

Les digrammes sont un outil conceptuel essentiel pour comprendre le monde des particules élémentaires et le modèle qui décrit les forces fondamentales agissant à l’échelle microscopique, à savoir le modèle standard. Les diagrammes de Feynman sont un outil très puissant permettant de décrire les interactions entre les particules étudiées dans la théorie quantique des champs. Dans les diagrammes de Feynman, les propagateurs ne sont pas des simples dessins, ce sont bien plus des instructions pour calculer, dans le cadre de la mécanique quantique, la probabilité qu’une particule située au point a se manifeste ensuite (éventuellement par un ordre de successions) au point b. Feynman eut l’idée radicale qu’une particule ne se limite pas à se déplacer en empruntant un seul chemin, mais en sondant en quelque sorte tous les chemins possibles, aussi bien ceux casuels et ondulés que ceux rectilignes.

Feynman a utilisé ces ingrédients de base – qui font fonction d’éléments (et de règles) de sens, que sont les propagateurs et les vertex, pour construire des processus (ou des systèmes de signification) plus complexes. On voit dès lors que toutes les forces dans la nature dérivent de diagrammes d’échange dans lesquels un photon (ou son analogue) est émis par une particule et absorbé par une autre particule. D’une manière générale, le diagramme est ici conçu en tant que forme d’un processus physique, un processus invisible et donc inaccessible à toute perception directe émanant uniquement de la vue, et son principal rôle est d’annoncer la force, en quelque sorte de l’objectiver. La force électrique entre deux électrons, par exemple, dérive d’un diagramme de Feynman où l’un des électrons émet un photon, lequel est ensuite absorbé par l’autre électron. En sautant d’un électron à l’autre, le photon (quanta de lumière) donne lieu à la force électrique et magnétique entre les deux particules.

En formant des réseaux de vertex et de propagateurs entrelacés, et même noués, on peut construire des diagrammes de Feynman de plus en plus complexes, pouvant représenter des processus qui comportent un nombre quelconque de particules. De ce point de vue, la théorie de Feynman propose un modèle de la matière qui va du simple au complexe.

Brève conclusion

Nous avons essayé de montrer que d’une manière générale, et plus particulièrement dans le cas des diagrammes de nœuds et des diagrammes de Feynman en électrodynamique quantique, les diagrammes n’ont pas été utilisés pour simplement « illustrer » quelque chose (objets et événements), mais plutôt comme des opérations symboliques (on pourrait dire, des opérateurs) de nature algébrique et topologique. De plus, les diagrammes permettent de montrer et connaître des propriétés topologiques de l’objet nœud concernant notamment leurs possibles transformations dans l’espace et leurs caractéristiques invariantes. D’ailleurs, une fois connues ces propriétés topologiques peuvent conduire à la découverte de nouveaux invariants algébriques des nœuds.

Les diagrammes ont un pouvoir gnoséologique car ils permettent d’explorer la structure interne de l’objet-nœud. Les diagrammes déploient la structure de l’objet, mais aussi du processus ou de la formule, en la projetant sur un espace de plus petite dimension, généralement le plan, où apparaissent clairement ses diverses interactions et articulations. Le diagramme donne à voir des changements que l’on peut effectuer dans la structure interne et dans la forme globale de l’objet.

Les diagrammes ne se limitent pas à offrir une image du monde tel qu’il nous apparaît, mais une construction symbolique et conceptuelle puissante, une clé de lecture et de réécriture des processus de la formation du monde « réel », une sorte de sémiodynamique ouverte de son devenir. De ce point de vue, le diagramme traduit la forme d’une manière de penser (ou d’une stratégie conceptuelle) que le physicien-géomètre est capable de donner à la matière, au monde physique. Cela revient à dire, en d’autres termes, que le diagramme constitue l’ensemble des qualités plastiques d’une pensée en train de se former comme modèle effectif, comme forme qui tend à s’objectiver dans des processus réels. Les diagrammes ont trois fonctions à la fois : (i) élucider des concepts en en déployant les articulations au sein d’une forme possible ; (ii) introduire de nouveaux concepts ; (iii) créer de nouvelles propriétés des objets que les diagrammes (graphes, arbres) modélisent.

On a vu, d’une manière non technique, que la structure mathématique de la physique des particules élémentaires se trouve exprimée dans la théorie quantique des champs. Les équations de cette théorie étant très difficiles et compliquées, il a fallu inventer un mode graphique pour pouvoir les « visualiser » et les appréhender. La pensée diagrammatique a ainsi ouvert la voie à de nouvelles méthodes et techniques de visualisation d’objets et phénomènes inaccessibles à la perception visuelle de tous les jours, et aussi aux expériences qu’on peut réaliser par des appareils même très sophistiqués. La visualisation présente ainsi un pouvoir explicatif supplémentaire par rapport à d’autres méthodes classiques utilisées dans les sciences mathématiques et physiques. Elle consiste dans la création d’images mentales des objets et des équations. C’est dire que certaines techniques de visualisation, notamment les diagrammes, se constituent en deux niveaux de représentation : le premier correspond à des modèles d’objets réels en tant qu’ils sont imaginés et non pas (directement) observés ; le second concerne les éléments qui forment les modèles eux-mêmes, c’est-à-dire les aspects graphique, dénotatif et connotatif. De ce point de vue, les diagrammes (comme les images, les dessins, les graphes…) donnent à « voir » ce qui n’est pas visible, par une création d’objets et de nouvelles articulations de sens.