Le immagini nei dati : modelli di estrazione e visualizzazione
Scienze dell’informazione e Intelligenza Artificiale : il contesto di riferimento.
Prima di affrontare alcuni dei concetti che legano complessità e immagini, è utile descrivere brevemente il contesto nel quale si muovono oggi le scienze dell’informazione e in particolare l’Intelligenza Artificiale.
- Note de bas de page 1 :
-
Questo paragrafo costituisce una rielaborazione della parte introduttiva del saggio di Massimo Buscema, Marco Intraligi, Guido Maurelli, Introduzione alla filosofia dei Sistemi Artificiali Adattivi e loro applicazioni, in SAAB Sistemi Artificiali Adattivi in Biomedicina n° 1, Gastroenterologia, Di Renzo Editore, Roma, 2005, Vol. I, pp. 104-163.
Sotto la denominazione di « Artificial Sciences » vengono oggi incluse una serie di discipline che hanno come obiettivo comune la comprensione dei processi naturali e/o culturali1. Questa operazione si realizza tramite un meccanismo di « ri-creazione » di tali processi utilizzando modelli automatici di simulazione. Si può affermare che nell’ambito delle Artificial Sciences il computer sembra avere una funzione analoga a quella della scrittura per la lingua naturale.
Queste scienze sono costituite da algebre formali per la generazione di modelli artificiali (strutture e processi), nello stesso modo in cui le lingue naturali sono dotate di una semantica, di una sintassi e di una pragmatica per la generazione di parole e testi.
Nelle lingue naturali la scrittura rappresenta la conquista dell’indipendenza della parola dal tempo, utilizzando lo spazio. Nelle Artificial Sciences il computer è la conquista dell’indipendenza del modello dal soggetto che lo ha ideato, attraverso l’automazione e / o l’azione. Così come, servendosi della scrittura, una lingua naturale può creare oggetti culturali che prima della scrittura erano impensabili (romanzi, poesie, testi di leggi, manuali ecc.), allo stesso modo le Artificial Sciences, utilizzando il computer, possono creare modelli automatici di computazione dotati di particolare complessità. Le lingue naturali e le Artificial Sciences, rispettivamente, le prime in mancanza della scrittura e le seconde in mancanza del computer, rimangono sistemi di comunicazione e di conoscenza molto limitati. Non a caso quelle culture che per diversi motivi non hanno fatto uso della scrittura, hanno avuto molte più difficoltà a tramandare il loro sapere. Ma, contemporaneamente, una scrittura che non si basa su una lingua naturale così come un modello automatico che non viene generato da un’algebra formale, appaiono entrambi come un insieme di incomprensibili scarabocchi.
Nelle Artificial Sciences la comprensione di un qualsiasi fenomeno, sia naturale che culturale, avviene in modo proporzionale alla capacità del modello artificiale automatico di ricreare la struttura di quel fenomeno. Più la comparazione tra processo originale e modello generato produce un esito positivo, più è probabile che il modello artificiale abbia esplicitato correttamente le regole di funzionamento del processo originale.
Questo confronto, tuttavia, non può essere effettuato in modo ingenuo. Sono necessari sofisticati strumenti di analisi per fare una comparazione attendibile tra processo originale e modello artificiale.
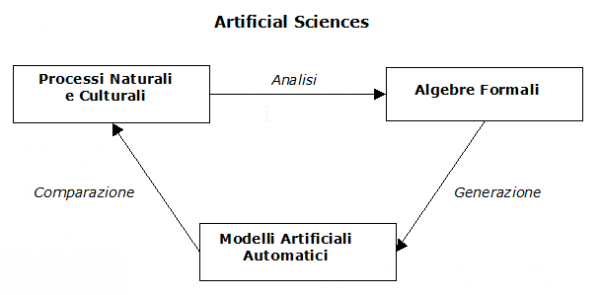
Gli strumenti di analisi utili per questa comparazione hanno il compito di confrontare le dinamiche di funzionamento del processo originale con quelle del modello artificiale, facendo variare contestualmente le rispettive condizioni al contorno. L’analisi dei processi sia naturali che culturali deve partire da una teoria che, adeguatamente formalizzata, è in grado di generare modelli artificiali automatici di tali processi. Al termine di questo percorso generativo i modelli automatici devono essere comparati con i processi originali di cui pretendono essere la spiegazione. Nel grafico della figura 1 è illustrata la dinamica di funzionamento di tale processo.
Fig. 1. Percorso generativo per l’analisi dei processi naturali e/o culturali, la generazione e la comparazione dei modelli artificiali
I modelli artificiali automatici per poter essere verificati e compresi necessitano di modi di visualizzazione. Tali modi a volte si rifanno a tecniche di rappresentazione ormai consolidate nella storia della scienza, altre volte necessitano di nuovi metodi che tendono a riprodurre fenomeni naturali e culturali attraverso tecniche di simulazione e visualizzazione in precedenza sconosciute.
Alcuni concetti nel rapporto complessità ed immagini
Per affrontare il rapporto tra complessità ed immagini abbiamo lanciato uno sguardo nell’insieme di concetti che riguardano tale rapporto, e ne abbiamo selezionati alcuni con lo scopo di tentare di illustrare come le componenti visive possono illustrare efficacemente le dinamiche dei fenomeni complessi. Abbiamo selezionato quattro coppie di concetti, ognuna delle quali evidenzia una peculiarità.
-
complesso Vs complicato ;
-
tempo ed evoluzione ;
-
visibile ed invisibile.
Complesso Vs complicato
I termini complesso e complicato nel linguaggio comune vengono spesso usati come sinonimi. Nel linguaggio scientifico identificano processi molto diversi. Ridotte ai minimi termini le differenze fra un sistema complesso e un sistema complicato possono essere riassunte in due semplici frasi :
-
in un sistema complesso il tempo è informazione, in un sistema complicato è rumore ;
-
il « gesto » di esistenza di un sistema complesso è centrifugo, quello di un sistema complicato è centripeto.
- Note de bas de page 2 :
-
Questo argomento è stato trattato nel saggio di Massimo Buscema e Guido Maurelli Immaginazione scientifica, rigore e ragionevolezza, « Atti del Convegno di Studi Tomo I. Ragione, ragionevolezza, esperienza (esperimento), dimensione oggettiva e storica della ricerca scientifica e giuridica » a cura di Augusto Cerri, Aracne Editrice, Roma 2007, pp. 171-200.
Proviamo a trarre una serie di conseguenze che approfondiscono le di differenze fra ciò si definisce sistema complesso e ciò che si definisce sistema complicato, a partire da queste due semplici frasi2.
Un sistema complesso è generato dalla interazione locale, cooperativa e competitiva, delle sue unità atomiche nel tempo. Diversamente in un sistema complicato le unità atomiche interagiscono sempre secondo determinate regole, che non cambiano nel tempo.
Le regole di un sistema complesso sono l’effetto prodotto dalla dinamica che si crea fra le unità atomiche in un certo arco temporale. In un sistema complicato, invece, le regole vengono stabilite a priori.
Un sistema può dirsi complesso quando gli effetti globali delle sue interazioni locali sono imprevedibili, e non è possibile analizzarle tramite logiche di causa-effetto. Normalmente gli effetti prodotti da un sistema complicato sono analizzabili tramite logiche di causa-effetto.
Un sistema complesso non segue delle regole, ma le genera dinamicamente nel tempo, mentre un sistema complicato deve necessariamente seguire una serie di regole predeterminate per poter funzionare.
Un sistema complesso ha la caratteristica di essere adattivo, cioè è sensibile al contesto, un sistema è complicato quando funziona allo stesso modo in qualunque contesto venga collocato.
In un sistema complesso il tempo è informazione. In un sistema complicato il tempo è rumore, e produce solo effetti negativi su se stesso.
La complessità di un sistema si genera dal basso verso l’alto, e il sistema si espande dall’interno verso l’esterno, secondo una logica centrifuga. Un sistema complicato, invece, si costruisce tramite una tecnica combinatoria per composizione di parti, il suo « gesto costruttivo » risponde ad una logica centripeta.
Un sistema complesso crea regole semplici e locali che si trasformano nel tempo. Un sistema complicato è una macchina combinatoria, non produce informazione, funziona in modo reversibile e tautologico.
In un sistema complesso i rapporti causa-effetto sono l’eccezione e non la regola ; nei sistemi complicati i rapporti causa-effetto sono la regola e non l’eccezione.
I sistemi complessi appartengono al mondo naturale, i sistemi complicati appartengono al mondo culturale, sono i prodotti dell’attività umana.
Proviamo ora a fare un esempio con il quale rendere più chiara questa differenza.
Pensiamo ad un soggetto umano, qualche anno fa ha fatto molto scalpore la scoperta del numero di geni che determinano l’organizzazione e il funzionamento dell’organismo umano. È emerso, infatti, che tale numero è assai inferiore a quello che si prevedeva. La stima si attesta tra i 30.000 e i 40.000 geni, in riferimento ai due studi più importanti a livello mondiale. Il numero dei geni è, quindi, circa un terzo di quello che si stimava fino alla fine degli anni novanta. È indubbio che un soggetto umano è un sistema complesso, probabilmente il sistema più complesso che noi conosciamo.
Prendiamo ora un aereo, come ad esempio un Boeing 747, che è composto da circa 200.000 parti elementari, quindi circa 5 volte il numero di geni presenti in un organismo umano. Si tratta di un oggetto che è in grado di volare, cioè può fare una cosa che non soggetto umano non è in grado di fare, ma non può considerarsi un sistema complesso, è semplicemente un sistema complicato.
L’esempio ci mostra che la quantità non è sinonimo di complessità. Esistono sistemi composti da una quantità enorme di parti, ma non per questo possono dirsi complessi. Nel nostro esempio il Boeing 747 è composto da molti più elementi di un soggetto umano, ma la sua complessità di funzionamento è imparagonabile con la complessità di funzionamento anche del più stupido degli uomini.
In secondo luogo le performance di volo dell’aereo, dopo il suo normale « rodaggio » nel quale raggiunge una sorta di efficienza ottimale, diventeranno lentamente sempre meno efficienti. Per un aereo il tempo funziona solo come fattore d’invecchiamento. Un pilota, invece, alla prima esperienza sarà poco efficiente, ma la sua capacità di guidare l’aereo sarà sicuramente migliorata dopo un certo numero di voli e, nel tempo, continuerà a migliorare.
I sistemi complessi usano il tempo per apprendere, i sistemi complicati al trascorrere del tempo si deteriorano.
Tempo ed evoluzione
Come abbiamo visto il tempo, o meglio l’uso del tempo, è un elemento fondamentale di discriminazione fra sistemi complessi e complicati.
Nei sistemi complessi è la dimensione attraverso la quale questi si evolvono, nei sistemi complicati è solamente un elemento di disturbo « rumore ».
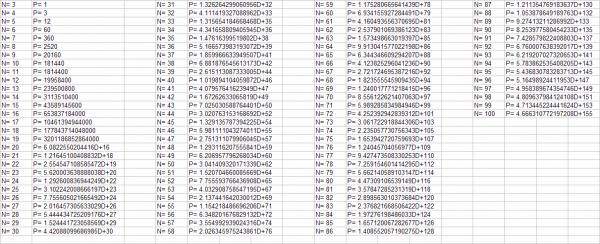
Un esempio può essere utile per far comprendere ai non matematici quanto il legame fra tempo, evoluzione e complessità sia molto stretto e in molti casi non dominabile. Prendiamo il cosiddetto problema del « commesso viaggiatore ». È descrivibile in questo modo : dato un insieme di punti distribuiti in uno spazio bidimensionale, trovare il percorso minimo per connetterli tutti, senza passare due volte nello stesso punto. Così descritto sembra un problema apparentemente semplice, ma invece nasconde effetti collaterali sorprendenti. La tabella sottostante fornisce un’idea numerica chiara del fenomeno con cui abbiamo a che fare.
Numero di percorsi che si generano aumentando il numero dei punti
Nella tabella appaiono 4 blocchi di due colonne affiancate, ogni blocco contiene il numero dei punti, con a fianco il numero di percorsi necessari per passare da ogni punto una sola volta toccando tutti i punti presenti sul piano.
Ad esempio :
N = 3 → P = 1
N = 4 → P = 3
N = 5 → P = 12
…….
N = 10 → P = 181.440
…….
N = 15 → P = 43.589.145.600
ecc.
Come si vede dalla tabella all’aumento del numero dei punti l’incremento del numero dei percorsi è esponenziale.
La formula è la seguente :
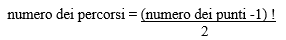
Si tratta, infatti, del fattoriale di un numero. Superati i 30 punti la risoluzione del problema diventa ingestibile da un computer estremamente potente che è in grado di fare miliardi di operazioni ogni secondo, qualora si dovessero esplorare tutti i percorsi e fare i relativi confronti per trovare la soluzione migliore. Si tratta di quella categoria di problemi cosiddetti np completi, la cui soluzione non può essere affrontata con un metodo di calcolo bruto, che esplora tutte le combinazioni, ma solo attraverso metodi euristici che procedono per approssimazione per tentare di raggiungere la soluzione ottimale.
Un problema del genere può essere affrontato con buon successo utilizzando modelli matematici ispirati al funzionamento del cervello, cioè i Sistemi Artificiali Adattivi. Si tratta di modelli automatici che effettuano la ricostruzione della dinamica di funzionamento di processi complessi attivando e sfruttando l’interazione locale dei microprocessi elementari che li compongono, in questo modo sono in grado di simulare efficacemente il funzionamento del processo originale. Tali modelli si auto-organizzano nel tempo e nello spazio, e si connettono in modo non lineare al processo globale di cui fanno parte, tentando di riprodurre la complessità attraverso la creazione dinamica di specifiche ed autonome regole locali, che si trasformano in relazione alle dinamiche del processo stesso. I Sistemi Artificiali Adattivi si presentano come teorie le cui algebre generative sono in grado di creare modelli artificiali che simulano i fenomeni naturali. Il meccanismo di apprendimento e di crescita dei modelli è simile all’evoluzione del processo naturale, cioè è esso stesso un modello artificiale comparabile con la nascita del processo naturale. Si tratta, quindi, di modelli teorici che assumono il « tempo di sviluppo » come un dispositivo formale del « tempo del processo » stesso.
- Note de bas de page 3 :
-
Massimo Buscema, « Genetic Doping Algorithm (GenD) : theory and applications », in Expert Systems, Blackwell Publishing, Vol. 2 n° 2, May 2004, pp. 63-79.
Utilizzando questi modelli è possibile affrontare il problema del commesso viaggiatore. L’applicazione di un algoritmo evolutivo ispirato a questi principi, scoperto al Semeion e denominato GenD3, consente di trovare una soluzione, che non è necessariamente la migliore in assoluto, ma che si approssima alla soluzione ottima, e soprattutto se confrontata con altri modelli che producono altre soluzioni, risulta la migliore.
Per capire meglio come funzionano questi sistemi mettiamo a confronto tre modelli, che hanno logiche di elaborazione diverse, e che trovano soluzioni diversamente efficaci.
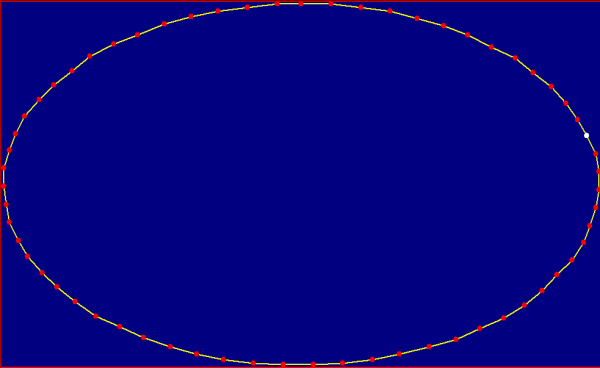
Il primo modello è l’algoritmo chiamato « Greedy », che funziona secondo una logica di buon senso molto semplice, così sintetizzabile : « Partendo da un punto qualunque mi sposto sempre a quello più vicino ». Questo tipo di logica in alcuni casi può risultare vincente, quando ci si trova di fronte ad una distribuzione di punti rappresentabile secondo la figura 2.
Fig. 2
In questo caso i punti sono distribuiti a cerchio. Risulta perciò facile, posizionandosi in uno qualunque dei punti e spostandosi in quello più vicino, trovare il percorso più breve. Come appare nella figura 3.
Fig. 3
Ma questo è un caso molto particolare di una distribuzione di punti. Certamente le città di una qualunque nazione non sono distribuite in questo modo sul territorio. Né in natura ci si trova normalmente di fronte a fenomeni che mostrano questa geometrica organicità.
Quando la distribuzione dei punti sul piano diventa più articolata le cose cambiano notevolmente, la semplice logica del « mi sposto sempre al punto più vicino » non è più efficace.
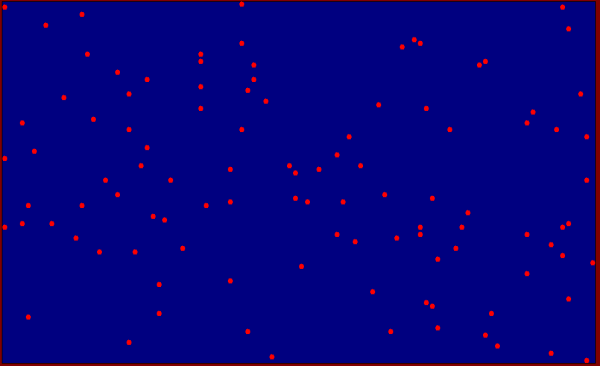
Nelle figure che seguono sono rappresentate tre soluzioni diverse del problema con 100 punti randomicamente sparsi su un piano.
Fig. 4 Iniziale distribuzione randomica dei punti
Fig. 4a Soluzione Greedy distanza del percorso km 892,05
Fig. 4b Soluzione Algoritmo Genetico distanza del percorso km 821,43
Fig. 4c Soluzione Algoritmo Evolutivo GenD distanza del percorso km 761,52
Confrontando le tre soluzioni e le rispettive distanze chilometriche appare evidente che il risultato prodotto dal modello Greedy è il più scarso dei tre. Il miglior risultato lo ottiene l’algoritmo evolutivo GenD, che mette in atto una logica di apprendimento e riesce a elaborare una visione d’insieme del problema approssimando la soluzione ottimale. In questo caso il modello riesce a rendere informativa la dimensione temporale simulando il meccanismo « dell’apprendere ad apprendere » tipico dei sistemi complessi.
Dal punto di vista visivo un soggetto umano è immediatamente in grado di comprendere che la figura prodotta dall’algoritmo GenD risulta la più efficace in quanto è completamente priva di incroci. Questo esempio mostra che l’occhio è in grado di intuire ciò che la ragione fa fatica a comprendere analiticamente, anche un esperto non sarebbe in grado di trovare il percorso migliore con il ragionamento analitico, mentre l’occhio vede d’istinto la soluzione migliore.
Visibile e invisibile
- Note de bas de page 4 :
-
Massimo Buscema, Sistemi ACM e Imaging Diagnostico – Le immagini mediche come Matrici Attive di Connessioni, Springer-Verlag Italia, 2006.
La luce nasconde. Sembra un’affermazione paradossale, ma non lo è. All’interno della numerosa famiglia dei Sistemi Artificiali Adattivi da un po’ di tempo sono stati scoperti dei modelli che sono grado di leggere le immagini in un modo completamente nuovo. Questi modelli sono stati messi a punto, da Massimo Buscema, nei laboratori del Semeion e hanno cominciato ad essere applicati in diversi campi, in particolare nel campo bio-medicale e nello specifico il cosiddetto settore dell’imaging diagnostico (mammografia, TAC, ecc.). In questo caso si tratta di una famiglia di sistemi, completamente indipendenti, che sono in grado di elaborare un’immagine facendone emergere la struttura sottostante e / o nascosta. Il loro nome è Active Connection Matrix (ACM)4, cioè sistemi che si basano su un principio di relazione attiva dei loro componenti minimi, che nell’imaging digitale sono i pixel.
- Note de bas de page 5 :
-
Tutte le considerazioni teoriche che seguono sono tratte dal libro di Massimo Buscema, Sistemi ACM e Imaging Diagnostico – Le immagini mediche come Matrici Attive di Connessioni, op. cit. pp. 6-8.
I sistemi ACM5 si basano sull’idea che ogni fenomeno visivo esprime nella sua forma una sua specifica geometria. Questa idea di base scaturisce da alcune considerazioni :
-
in ogni immagine digitale i pixel e le loro relazioni contengono il massimo dell’informazione disponibile per quella immagine ;
-
la posizione che in un’immagine ogni pixel occupa rispetto agli altri, è un’informazione strategica per la comprensione del contenuto informativo di quella immagine ;
-
in un’immagine la luminosità di ogni pixel, la sua posizione e le sue relazioni con gli altri pixel definiscono il contenuto informativo completo di quell’immagine, ovvero della dinamica con cui l’oggetto reale e le onde elettromagnetiche hanno interagito ;
-
le relazioni di ogni pixel con gli altri pixel della stessa immagine dipendono dalla dinamica delle connessioni che collegano ogni pixel con i pixel del suo intorno locale. Tale dinamica risente fortemente del modo di interagire dell’oggetto con la luce che lo investe, e risulta determinante ai fini dell’evidenziare anche le informazioni che sfuggono all’occhio umano, osservando l’immagine sorgente.
Queste considerazioni hanno implicazioni notevoli.
La prima consiste nello stabilire una differenza tra contenuto informativo di un’immagine e il suo significato culturale. Il secondo dipende dal primo, ma lo integra con altre conoscenze e abitudini di codifica non presenti nell’immagine né desumibili direttamente da queste. Tali conoscenze sono dipendenti, invece, dalla cultura dell’osservatore, dal contesto in cui esso è inserito e dall’uso che intende fare delle informazioni rappresentate nell’immagine. Ad esempio un medico radiologo è abituato ad interpretare una radiografia in un modo diverso da come può farlo un qualunque altro individuo che non è radiologo. La forma irregolare di una macchia su una radiografia, per il radiologo può indicare la presenza di un tumore, per una persona comune è solo una macchia simile alle altre. Il contenuto informativo che viene legato all’immagine della radiografia è determinato dalle conoscenze del medico, e dalla esperienza acquisita sul campo.
I sistemi ACM operano sul contenuto informativo e non sul suo significato culturale.
La seconda considerazione riguarda il processo di generazione del contenuto informativo di un’immagine. Da quanto detto ne deriva che il contenuto informativo di un’immagine è il processo tramite il quale i singoli pixel interagiscono localmente e in parallelo nel tempo. Di conseguenza il contenuto informativo di una singola immagine non è nel processo, né alla fine del processo dell’interazione locale dei suoi costituenti primi (i pixel), ma è il processo stesso. In ogni immagine, quindi, l’interazione locale dei suoi pixel nel tempo è, in certe condizioni, parte del contenuto informativo dell’immagine stessa ; quel contenuto informativo rimasto impresso nei pixel, durante il tempo di esposizione dell’oggetto alla luce che lo ha investito, rappresentativo della loro dinamica di interazione.
La terza considerazione riguarda le connessioni locali di ciascun pixel con i pixel del suo intorno. Ogni immagine è una rete di pixel connessi localmente. È sufficiente un intorno di raggio 1 per garantire che l’intera immagine sia una rete totalmente connessa di pixel. Questa esigenza di connettività incrementa la dimensionalità di tutti i pixel di un’immagine.
Il nome Matrice Attiva delle Connessioni significa, quindi, che ogni immagine è considerata come una matrice / rete connessa di elementi / pixel che si sviluppa nel tempo. Trasformare ogni immagine in una matrice di elementi connessi che attivamente si trasforma nel tempo equivale a rendere visibile il suo contenuto informativo. In altre parole, una immagine anche se appare statica conserva dentro di sé tutte le informazioni del proprio contenuto informativo. Quest’ultimo non è statico, perché esprime la dinamica delle interazioni locali tra i pixel costituenti l’immagine stessa, e per fare ciò ha bisogno di potersi esprimere tramite il tempo : è come se l’immagine di partenza nascondesse nel proprio interno un filmato che per poter essere visto deve, ovviamente, scorrere nel tempo.
Nei sistemi ACM alle dimensioni originarie delle immagini vengono, quindi, aggiunte 2 dimensioni nuove : la connessione locale W e il tempo T. Le coordinate originarie di un’immagine sono costanti e danno un contributo costante al valore di luminosità L, mentre le connessioni W nel tempo si modificano e, direttamente o indirettamente, modificano anche la luminosità di ogni pixel.
In termini pratici : data un’immagine bidimensionale di M×N pixel, la sua traduzione nel sistema ACM la trasforma in una matrice di M×N×Q×T pixel, dove Q è il numero delle connessioni tra ogni pixel con quelli del suo intorno e T è il numero di istanti discreti dall’inizio alla fine del processo. Quindi, se il valore della connettività tra i pixel varia nel tempo, è evidente che in ogni istante di tempo T si potranno generare T matrici diverse di Q pixel, ciascuna delle quali renderà visibili le sole relazioni che esistono tra ogni pixel e ognuno dei suoi vicini.
I sistemi ACM, quindi, rimodellano un’immagine digitale qualsiasi tramite tre operazioni :
-
trasformano l’immagine originale in una rete connessa di pixel ; quindi aggiungono una dimensione all’immagine stessa, la dimensione W delle connessioni tra un pixel e i pixel del suo intorno ;
-
applicano all’immagine trasformata delle operazioni locali, deterministiche e iterative che trasformano direttamente o indirettamente la luminosità originaria di pixel e / o le loro connessioni ; quindi aggiungono all’immagine originaria un’ulteriore dimensione T : il tempo ;
-
terminano questo processo quando la funzione di costo sulla quale sono fondate le operazioni di trasformazione dell’immagine è soddisfatta ; quindi considerano finito il tempo delle trasformazioni quando il processo stesso di trasformazione si stabilizza in modo autonomo.
Se le varie immagini che si succedono dipendono dalle connessioni tra i propri pixel, se le operazioni di trasformazione sono locali, deterministiche e iterative, e se il processo trasformativo tende autonomamente verso un attrattore stabile, allora il processo di trasformazione dell’immagine è esso stesso parte del contenuto informativo globale di quella immagine.
- Note de bas de page 6 :
-
Massimo Buscema, Sistemi ACM e Imaging Diagnostico – Le immagini mediche come Matrici Attive di Connessioni, op.cit.
La prima ipotesi sulla quale, quindi, si fondano i sistemi ACM è la seguente : « ogni immagine a N dimensioni, trasformata in una rete connessa di unità che si sviluppano nel tempo, tramite operazioni locali, deterministiche e iterative, può mostrare, in uno spazio dimensionale più ampio, delle regolarità morfologiche e dinamiche che nelle dimensioni originarie sarebbero non visibili oppure qualificabili come rumore »6.
Questa descrizione introduttiva era necessaria per sintetizzare alcune delle ipotesi di base su cui si fondano i sistemi ACM. Consentendo così al lettore di osservare i risultati scaturiti dalle elaborazioni di immagini mediche, apprezzandone la capacità di estrarre informazione nascosta, cioè rendere « visibile » ciò che risulta « invisibile » all’occhio umano.
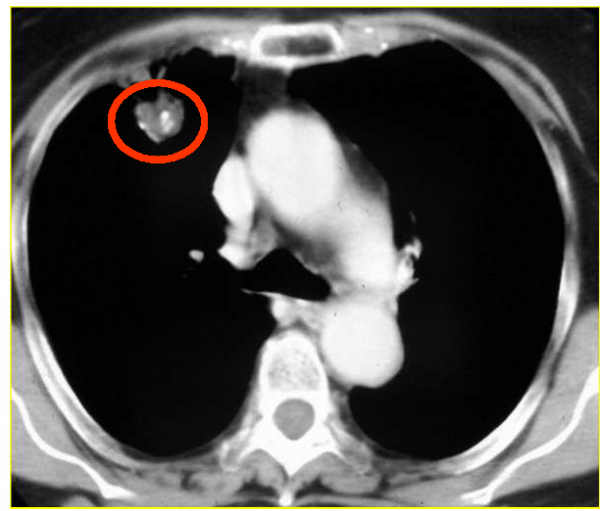
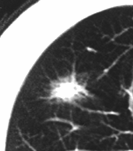
Nel primo esempio, illustrato dalla figura 5, è rappresentata una coppia d’immagini, l’immagine a sinistra è l’immagine sorgente, quella a destra è l’immagine elaborata con uno dei sistemi ACM.
Fig. 5a : Immagine sorgente : TAC
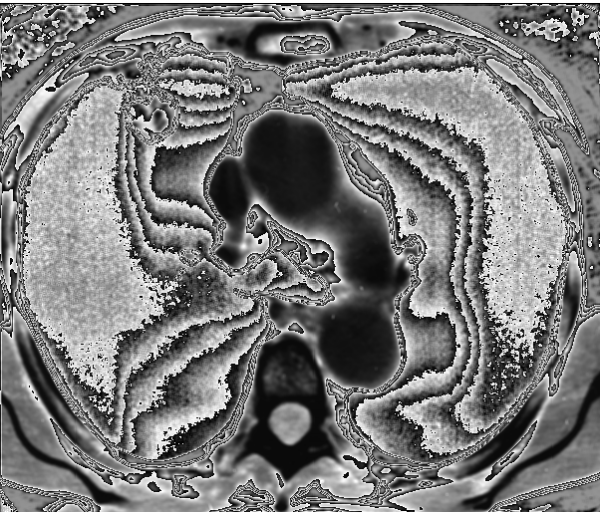
Fig. 5b Immagine elaborata : ACM-CM Rem
In questa prima coppia d’immagini siamo in presenza di un’immagine TAC al torace che rappresenta la fetta di un polmone di un paziente, nel quale è presente un tumore maligno raffigurato, in alto a sinistra, da un nodulo a margini irregolari (evidenziato dal cerchietto rosso). Nell’elaborazione effettuata con gli algoritmi di uno dei modelli ACM (CM Rem) si può osservare che tutta la zona nera dell’immagine originale si è trasformata in una zona complessa popolata da una serie di onde irregolari che la attraversano. Da un punto di vista medico l’osservazione di questo fenomeno ha portato a riflettere sulla possibilità che il sistema sia stato in grado di portare alla luce la struttura dei vasi linfatici, lavorando sulle microdifferenze d’intensità del nero che l’occhio umano non è in grado di percepire.
- Note de bas de page 7 :
-
La spiegazione dettagliata dell’algoritmo J-Net è contenuta nella recente pubblicazione di Massimo Buscema, Luigi Catzola, Enzo Grossi, « Images as Active Connection Matrixes : the J-Net System », in IC-MED (International Journal of Intelligent Computing in Medical Sciences), Vol. 1, n° 3, Issue 1, p. 187-213, 2007, TSI Press USA.
Un secondo esempio è rappresentato da un nuovo algoritmo che appartiene alla famiglia dei sistemi ACM, ideato da M. Buscema e denominato J-Net7.
J-Net è un algoritmo in grado di identificare i bordi di immagini complesse, dotate di contorni particolarmente sfumati e cariche di « rumore visivo ». Riesce a definire lo scheletro di una figura sfruttando unicamente la luce riflessa dell’immagine. Sembra in grado di delineare una traiettoria evolutiva di alcune patologie in ambito medico a partire da specifiche immagini radiografiche statiche.
Si è scoperto che durante l’elaborazione di un’immagine assume una notevole rilevanza l’introduzione di un parametro alfa (α) che determina la sensibilità del modello alla luminosità dell’immagine, regolando diversamente e indipendentemente la scalatura dei valori. In questo modo il ricercatore, prima dell’elaborazione, può decidere la « messa in sintonia » del modello, attraverso il parametro α, decidendo di evidenziare diversi tipi di bordi nell’immagine da elaborare. Questa possibilità di sintonizzazione, derivata dai diversi valori assunti dal parametro α, è particolarmente interessante in quanto evidenzia che la radiografia di un tumore, colto come luogo di luminosità particolare, può essere bordato così come appare nel suo massimo della luminosità, ma anche nelle diverse luminosità periferiche che appaiono intorno al tumore. Queste luminosità sembrano in grado di predire gli stati successivi di avanzamento del tumore, cioè indicarne le dinamiche di sviluppo.
Dalle prime analisi mediche sembra che queste diverse luminosità siano collegate al modo in cui il tumore tende a muoversi. Una stessa immagine può essere elaborata tramite J-Net con diverse soglie α in modo indipendente. Le immagini elaborate con diverse soglie α porranno in evidenza immagini finali con figure diverse. I fattori α più bassi evidenzieranno solo le figure dotate di una luminosità più intensa, mentre fattori α più grandi porranno in evidenza solo le figure dotate di una luminosità sempre meno intensa.
Diversi valori di α, quindi, effettuano sulla immagine assegnata una scansione delle diverse intensità luminose.
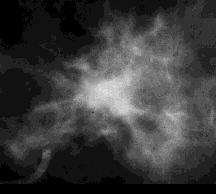
Se prendiamo, ad esempio, la radiografia di una « massa tumorale » evidenziata in una mammografia si possono osservare i diversi tipi di elaborazione che si ottengono intervenendo sul parametro α.
Fig. 6 Particolare di massa spicolata proveniente da una radiografia al seno
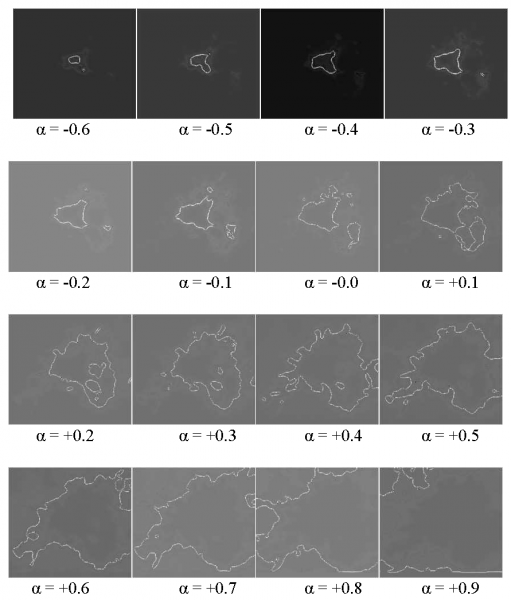
Fig. 7 Elaborazioni sulla immagine in figura 6 con diversi parametri di α
Se in ambito medico è possibile stabilire una corrispondenza tra l’intensità luminosa dell’immagine e l’attività della patologia, allora è possibile utilizzare le diverse scansioni di J-Net per individuare un ordine temporale di sviluppo della patologia stessa. La sequenza di elaborazioni, ottenute modificando il parametro α, visualizza tale fenomeno.
Un’altra serie di esperimenti sono stati fatti sui tumori ai polmoni. In questi casi si suppone che la diversa intensità luminosa presente nella tomografia computerizzata rifletta le zone dove il tumore è più attivo. Nel caso dei tumori maligni le parti più periferiche possono sembrare all’occhio umano scure come lo sfondo, mentre in realtà dovrebbero presentare « ombre leggere » di luminosità, che indicano le strategie di esplorative e diffusive del tumore stesso. Queste microvariazioni di luminosità possono essere così sottili che altri algoritmi di analisi potrebbero facilmente classificarle come « rumore » ed eliminarle.
Il sistema J-Net sembra capace cogliere delle microvariazioni di luminosità, riuscendo a distinguere i casi in cui tali microvariazioni dello sfondo rappresentano semplice rumore da quelli in cui le oscillazioni rappresentano un modello di immagine appena accennato.
La scansione effettuata da J-Net sull’immagine originale, tramite la variazione del parametro α, si è dimostrata capace di far emergere alcune forme di sviluppo di tumori ai polmoni con uno o due anni di anticipo.
- Note de bas de page 8 :
-
Buscema M, Catzola L, Grossi E, « Images as Active Connection Matrixes : the J-Net System », in IC-MED (International Journal of Intelligent Computing in Medical Sciences), Vol. 1, n° 3, Issue 1, TSI Press USA, 2007, pp. 187-213.
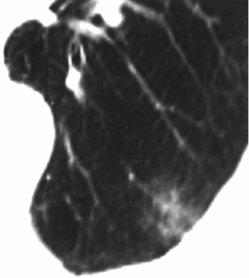
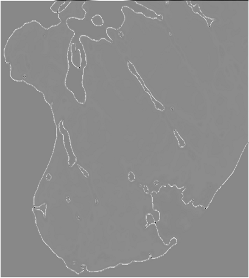
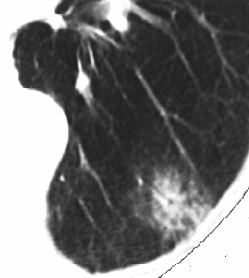
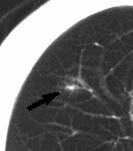
Mostriamo le immagini (Fig. 8) di due esperimenti realizzato su questa patologia. Provengono da un articolo scientifico pubblicato da alcuni ricercatori giapponesi su una rivista internazionale e riprese nell’articolo pubblicato da alcuni ricercatori del Semeion sul sistema ACM-JNet.8
Fig. 8a paziente al tempo 0
Fig. 8b elaborazione J-Net su 8a
Fig. 8c paziente un anno dopo
Nel primo esperimento l’immagine (8a) mostra un tumore (adenocarcinoma) di un paziente di 74 anni, rispetto alla quale i medici non ritengono di poter confermare una diagnosi di tumore certa. L’immagine (8c) mostra l’immagine dello stesso paziente effettuata dopo circa un anno, nella quale si evidenzia un avanzamento del tumore consentendone una diagnosi certa. L’immagine (8b) intermedia è costituita dall’elaborazione di J-Net (parametro α =0.4) effettuata sul primo originale (8a), dove si può notare come i contorni della zona tumorale siano molto somiglianti alla forma che il tumore assumerà un anno dopo.
Fig. 9 paziente al tempo 0
Fig. 9b elaborazione J-Net su 9°
Fig. 9c paziente 3 anni dopo
Nel secondo esperimento (Fig. 9) è stata seguita la stessa procedura. In questo caso si tratta di un altro paziente di 64 anni che nell’immagine (9a) presenta la possibilità di un adenocarcinoma non certo. Nell’immagine (9c) la tomografia computerizzata, effettuata dopo circa 3 anni, mostra l’evidente incremento dell’area tumorale. Nell’elaborazione, sull’immagine del paziente al tempo 0, effettuata con J-Net (parametro α =0.4) l’immagine (9b) descrive con buona precisione lo sviluppo del tumore dopo tre anni.
I sistemi di elaborazione della famiglia ACM sono stati applicati anche ad immagini non appartenenti all’ambito medico. Facciamo un ultimo esempio elaborando l’immagine del pianeta Saturno, utilizzando l’algoritmo Top-Net.
Nella figura 10 abbiamo un’immagine di Saturno registrata da un potente telescopio, che consideriamo l’immagine sorgente.
Fig. 10 Immagine sorgente di Saturno
Nella figura 11 abbiamo il risultato finale dell’elaborazione sull’immagine sorgente effettuata con l’algoritmo Top-Net del sistema ACM.
Fig. 11 Immagine di Saturno elaborata dal sistema ACM
Osservando attentamente queste due immagini si può notare che nell’immagine sorgente si vede Saturno sospeso nel buio dell’universo senza altri elementi che lo circondano. Nell’elaborazione effettuata con il sistema ACM Top-Net emergono chiaramente dei punti che identificano delle stelle presenti nell’immagine sorgente, ma non percepibili dal telescopio che le ha registrate.
Può essere utile, ora, vedere su che cosa lavora l’algoritmo per raggiungere questo risultato. Nella tabella che segue (Fig.12) è mostrata una piccola parte dell’immagine sorgente di Saturno in digitale. Sono questi i numeri su cui il sistema lavora per evidenziare e captare quelle microdifferenze che non appaiono all’occhio umano, ma che svelano oggetti presenti nell’immagine originaria.
Fig. 12 Parte dell’immagine digitale di Saturno
In questo passaggio è contenuta la strutturale « trasformazione intelligente » che determinati modelli di elaborazione sono in grado di produrre riconsegnando alla componente visiva una nuova struttura sintattica, restando nell’attesa di una semantica che ne consentirà l’uso funzionale.
Conclusioni
Ogni struttura, sia vivente che non vivente, in natura si manifesta attraverso una forma, ogni forma si manifesta attraverso un’immagine. L’occhio umano è lo strumento più sofisticato per comprendere le immagini. I modelli matematici, che simulano le logiche di funzionamento dell’occhio per analizzare la struttura delle immagini, sembrano costituire un buon sistema per comprendere le dinamiche della natura.
Nota
Tutte le immagini provengono da elaborazioni prodotte con i software di ricerca del Semeion (Semeion©), in particolare :
GenD TSP software, Buscema M, (v. 3, 1998-2006 Semeion©).
ACM software, Buscema M, (v. 12.5, 2005-2009 Semeion©).