La Fonction de Transfert Optique (FTO)

Avertissement – Le texte qui suit n’est pas un exposé détaillé de la FTO. Il émane d’un scientifique qui fait un usage constant des images dans le cadre de sa discipline (la Chimie) et qui souhaite rassurer les sémioticiens sur le sérieux de leur emploi, qui n’est ni naïf, ni aveugle, ni inconscient des pièges que tendent les distorsions et déformations inévitables du signal. La FTO est un des outils (sans doute le meilleur à ce jour) dont on dispose pour juger de la qualité et de la validité d’une image. L’exposé qui suit se borne donc à présenter succinctement à des non-spécialistes une théorie débarrassée de la partie la plus lourde de son appareil mathématique. Les personnes intéressées sont invitées à se référer à l’ouvrage suivant : Tom L. Williams, The Optical Transfer Function of Imaging Systems, sur lequel je me suis largement appuyé. La plupart des illustrations proviennent de ce traité.

1. Introduction

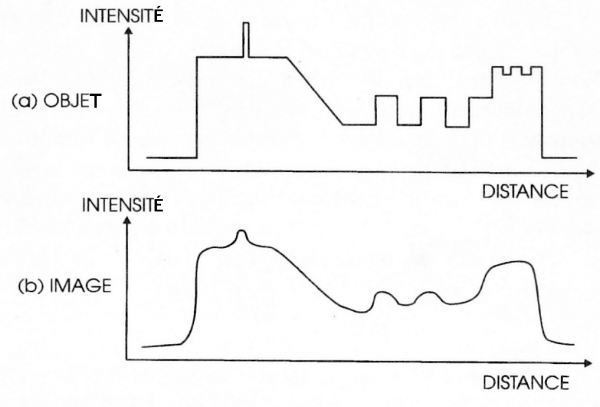
De nombreux appareils produisent ou transforment des images. Beaucoup sont des dispositifs optiques, mais certains produisent une image visible à partir de rayonnements invisibles (par exemple la caméra thermique ou les écrans X). L’œil lui-même, dernier maillon d’une chaîne parfois longue, doit aussi être considéré comme un de ces appareils. Tous introduisent des aberrations, des déformations, des distorsions, du bruit (fig.1).

Fig. 1 - EXEMPLE DE DÉGRADATION

Dans un but de comparaison évaluative, il est donc important de disposer d’outils précis pour déterminer la qualité d’une image produite par l’un de ces dispositifs ou, mieux encore, par une cascade de ces appareils. La Fonction de Transfert Optique (FTO) est un de ces outils. En termes techniques la « qualité » d’une image consiste en la reproduction fidèle de la distribution des intensités relatives de la scène originale. Quels en sont les facteurs et comment peut-on les mesurer ? Peut-on déterminer la FTO nécessaire pour l’accomplissement d’une tâche donnée ? L’œil est-il supérieur à la machine ?

2. Les paramètres de mesure

Lorsqu’on parle de la qualité d’une image, on vise généralement la finesse des détails résolus ou la netteté des bords, encore que ce dernier aspect soit davantage prisé pour l’image d’un bâtiment que pour un portrait. Il s’agit d’un complexe de facteurs très subjectif et relatif à une tâche déterminée, telle que « produire une photo agréable », ou permettre de suivre un objet déterminé à une distance déterminée, etc. On s’attachera donc à déterminer des paramètres plus précis, quitte à les regrouper ensuite en fonction de l’objectif poursuivi.

2.1 Le contraste

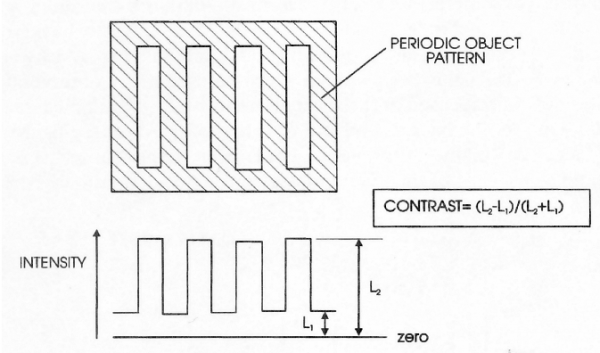
Toute perception étant contrastuelle, il s’agira de restituer au mieux les contrastes de la scène originale. On a d’abord mesuré le seuil de contraste permettant à l’œil de détecter un disque brillant sur fond sombre, mais on a rapidement conclu qu’il fallait améliorer cette technique et utiliser plutôt un réseau périodique constitué d’un graticule, plaque portant des bandes parallèles, de même largeur et alternativement noires et blanches. Illuminée, une telle plaque renvoie à l’œil une onde carrée (non une sinusoïde) présentant deux niveaux de luminance L1 et L2 (fig. 2).

Fig. 2 - DÉFINITION DU CONTRASTE POUR UN RÉSEAU PÉRIODIQUE

Le contraste C est alors défini par 

C = ^{L2 – L1} /_{L2 + L1}

et la fréquence spatiale, soit le nombre de paires de bandes par unité d’angle de vision, en cycles par degré (c/deg).

N.B. Ne pas confondre l’Illuminant ou lumière reçue par une image, avec la Luminance ou lumière réémise par cette image.

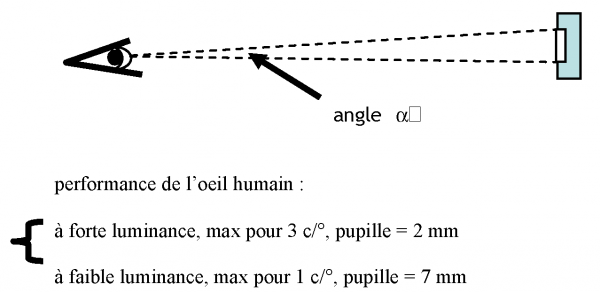
On constate que la performance de l’œil diminue avec la luminance, mais selon des courbes à maximum. Par exemple un maximum de 3 c/deg à forte luminance tombe à 1 c/deg à faible luminance, une sensibilité dix fois inférieure (fig. 3).

Fig. 3 - FRÉQUENCE SPATIALE (seuil de contraste en cycles par degré)

Selon Tyler on ne peut plus distinguer les irrégularités d’une surface si leur fréquence spatiale dépasse 4 c/deg.

Plusieurs conséquences découlent de ces observations.

Le diamètre de la pupille (iris) peut atteindre 7 mm sous des luminances très faibles. Par analogie, les dispositifs optiques peuvent être, eux aussi, caractérisés par un diamètre de pupille. On calcule alors que télescopes, lunettes, périscopes, jumelles… destinés à grandir 10X devraient avoir un diamètre d’objectif, plutôt encombrant, de 70 mm. Le compromis habituel, qui limite ce diamètre à 40 mm, entraîne donc une perte de performance sous lumière faible.

Inversement, lorsque l’image aboutit à un appareil électronique, p. ex. un tube à rayons cathodiques (TRC), la luminance maximum réalisable est limitée. Elle l’est encore davantage si l’image est projetée sur un grand écran, qui présente lui aussi ses caractéristiques. Le cas le plus critique est celui des cristaux liquides et des diodes électroluminescentes, avec lesquelles il est difficile d’obtenir des niveaux suffisants de luminance.

2.2 La distorsion

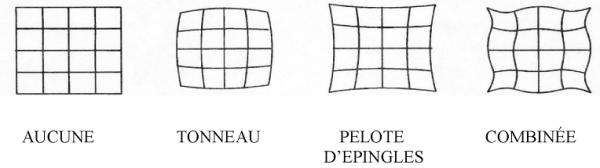
Un réseau de lignes parallèles et équidistantes est rarement reproduit fidèlement. On a donné aux divers types de distorsion des noms imagés (fig. 4).

Fig. 4 - TYPES DE DISTORSION

Souvent la distorsion est très asymétrique. La tolérance vis-à-vis de la distorsion varie avec l’application envisagée : les TV et les caméras sont des dispositifs moins exigeants.

2.3 La limite de résolution

Il y a toujours dégradation des images, en particulier par atténuation des contrastes et par étalement des zones de forte intensité, ce qui a pour effet de rendre flous les bords. Quelle que soit la perfection des appareils il y a une limite physique à leur pouvoir de résolution : c’est la diffraction, étudiée par Lord Rayleigh (v. Biémont, 1996). Un exemple banal est montré fig. 5.

Fig. 5 – Diffraction : Faire passer un rayon de lumière polarisée dans la fente d’une lame de rasoir.

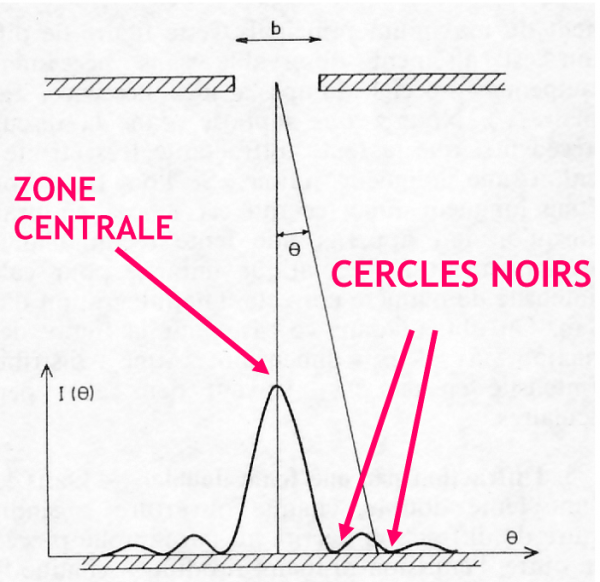
Une source ponctuelle n’est pas vue comme un point mais selon une figure en forme de disque comportant un anneau noir autour du point lumineux central (le disque d’Airy, v. fig.6).

Fig. 6 - FIGURE DE DIFFRACTION À PARTIR D’UNE SOURCE PONCTUELLE

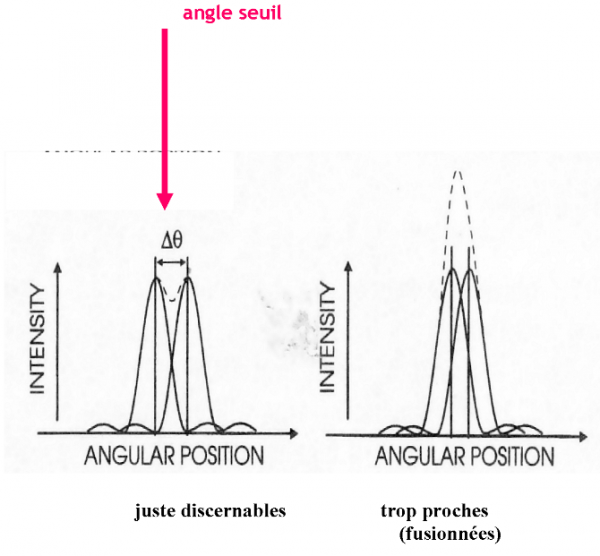
Lorsqu’on cherche à distinguer deux sources ponctuelles proches, on bute sur la limite de résolution, qui est la distance angulaire pour laquelle le pic de la source A correspond à l’anneau noir de la source B (fig.7) et réciproquement.

Fig. 7 - LIMITE DE RÉSOLUTION SELON RAYLEIGH (cas de deux fentes)

Dans ce cas il y a entre les deux pics un petit creux permettant tout juste de les séparer.

Un moyen simple d’évaluer le pouvoir de résolution d’un appareil est de regarder à travers lui un jeu de mires calibrées, comme si elles étaient un objet. La méthode est simple mais non exempte de défauts. Ce n’est en tout cas pas une bonne idée d’utiliser des figures à fort contraste, car les appareils sont le plus souvent chargés d’enregistrer des spectacles à faible contraste.

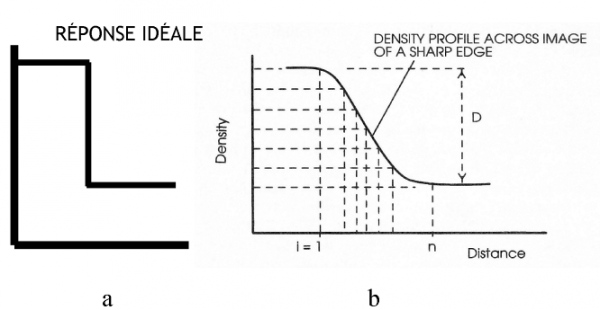
2.4 L’acutance

Ce critère a été développé pour la photographie. On photographie un bord vif puis on mesure, à l’aide d’un scanneur microphotométrique, le profil de densité de son image (fig. 8).

Fig. 8 - L’ACUTANCE PHOTOGRAPHIQUE

Au lieu d’une chute carrée (a) on enregistre une courbe (b) à partir de laquelle on peut calculer un indice appelé acutance, basé sur le gradient de densité mesuré le long de la courbe.

Conclusion : il existe plusieurs critères et méthodes d’évaluation possibles, et la FTO (qui sera détaillée au §4) en est une autre, beaucoup plus fondamentale. Une attitude logique est de se baser d’une part sur la FTO et d’autre part sur une analyse du bruit telle qu’indiquée ci-après.

3. Le bruit

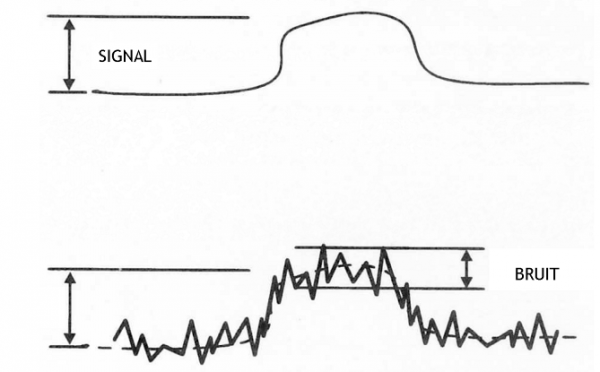
Les mesures montrent que pour une cible de dimension angulaire donnée la sensibilité au contraste est proportionnelle à √L (où L est la luminance), ce qui est conforme à la loi de Weber-Fechner. On interprète ce fait en admettant que l’aptitude de l’œil à détecter une configuration est une fonction du rapport signal / bruit dans l’image qui se forme sur la rétine (fig. 9).

Fig. 9 – EFFET DU BRUIT SUR UN SIGNAL

On définit le signal comme la différence entre le nombre de photons N_c issus de la cible et le nombre de photons N_f issus d’une surface équivalente du fond : dN = N_c – N_f .

D’autre part on définit le bruit comme la fluctuation statistique de N_f , dont on peut montrer qu’elle est égale à √N_f .

Le rapport signal / bruit, représentant le seuil de contraste, sera donc dN / √N_f. La sensibilité au contraste sera alors définie comme l’inverse du seuil, de sorte qu’elle sera proportionnelle à √N_f, lequel est à son tour proportionnel à L_f (luminance du fond) : CQFD.

La source ultime du bruit qui affecte l’image formée sur la rétine est ainsi la fluctuation dans le flux de photons qui y parvient. Mais ce n’est pas la seule cause de bruit. On en distingue deux types :

• le bruit fixe dans le temps : p.ex. le grain d’une photo, la grille d’un écran TV, la configuration d’un faisceau de fibres optiques…

• le bruit variable dans le temps : outre la fluctuation du flux de photons sur la rétine, celle de la réponse de la rétine à ce flux et celles des systèmes électroniques.

Cette distinction est capitale car l’œil les traite différemment. L’œil est en effet à la fois un filtre spatial et un filtre temporel. En tant que filtre spatial il tend à adoucir et à réduire les variations spatiales d’intensité lumineuse : cette aptitude réduit les deux types de bruit. En tant que filtre temporel il tend à moyenner, ou à intégrer, les changements, ce qui réduit le bruit temporel sans affecter l’autre.

4. La FTO

4.1 Le principe

Les images présentant une infinie diversité de formes aussi bien que de gradations d’intensité et de couleur, il convient de trouver un indice les reflétant toutes avec une égale fidélité : on le cherchera donc dans la caractéristique fondamentale de la perception, celle d’être contrastuelle. Pour pouvoir être traité commodément par des méthodes mathématiques, le test devrait idéalement fournir un signal sinusoïdal. L’image type, dite cible, présentée à chaque appareil pour en évaluer les performances sera constituée d’un graticule comportant des fentes parallèles et équidistantes. Ce dispositif se rapproche du signal sinusoïdal, mais ne livre évidemment qu’une onde carrée. Heureusement, une analyse dite de Fourier permet de la ramener à une somme de sinusoïdes. La déformation d’une sinusoïde peut porter sur son amplitude (amplification ou atténuation) ou sur sa phase (déphasage : léger décalage dans le temps). Il existe ainsi une fonction de transfert qui caractérise la comparaison entre les valeurs dans les images de départ et d’arrivée. La reproduction du contraste s’appelle FTM (fonction de transfert de modulation). La fonction de transfert de phase (FTP) produit des déformations beaucoup moins significatives et est généralement négligée. Elle existe néanmoins et peut être mesurée, mais ne sera pas abordée dans le présent exposé. Ensemble, la FTM et la FTP forment la FTO, fonction de transfert optique.

4.2 La réponse en fréquence

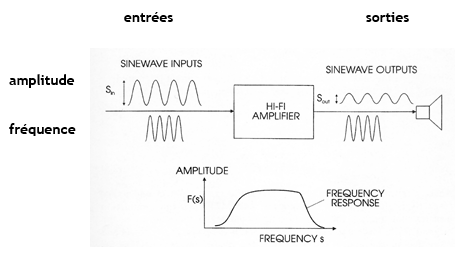
Les performances d’un appareil vont varier en fonction de la fréquence du signal d’entrée. L’analogie avec la Haute-Fidélité en reproduction musicale est ici instructive. Un appareil est dit HiFi s’il présente un plateau bien horizontal entre les fréquences limites des sons audibles (fig. 10).

Fig. 10 - LA RÉPONSE EN FRÉQUENCE (cas d’un signal sonore)

Il en va de même pour des lentilles, sinon que cette fois la sinusoïde est produite par un réseau, dont la fréquence spatiale se mesure en cycles par unité d’angle. C’est donc l’intensité lumineuse qui variera sinusoïdalement, et on pourra en comparer les valeurs d’entrée et de sortie en appelant contraste C le rapport suivant :

C = ( I_max – I_min ) / ( I_max + I_min )

Le contraste C₀ de l’objet est relié au contraste C₁ de son image par la fonction de transfert FTM. Il y a une FTM pour chaque valeur de la fréquence spatiale dans le signal d’entrée.

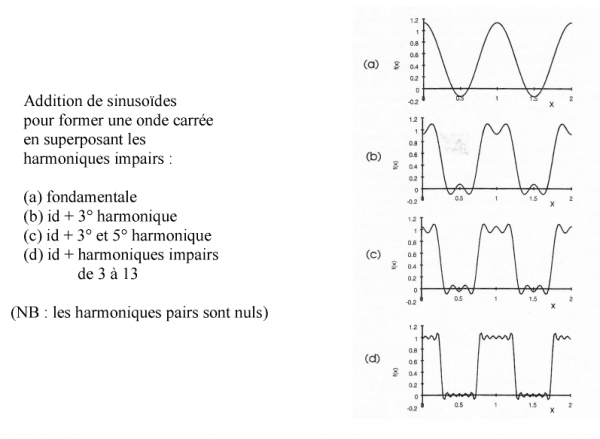
La transformation de Fourier permet de représenter un signal de forme absolument quelconque (même une onde carrée !) en la somme d’une série de sinusoïdes, constituée d’une fondamentale et d’un nombre infini de ses harmoniques. En pratique des simplifications intéressantes sont possibles. Tous les harmoniques pairs sont nuls, et les harmoniques impairs deviennent vite négligeables, comme le montre intuitivement la fig. 11. En outre la transformation de Fourier est réversible.

Fig. 11 - TRANSFORMATION DE FOURIER

4.3 Les avantages du système

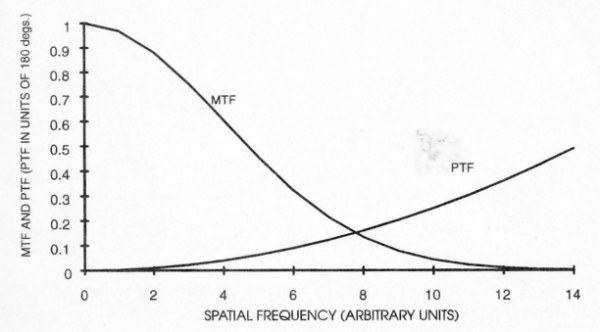
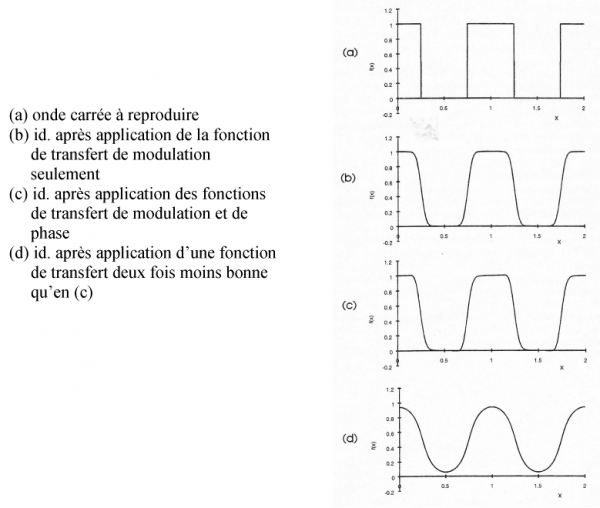
Toute courbe, spatiale ou temporelle, peut être soumise à cette technique, c.à.d. pratiquement tout signal d’entrée. Connaissant la FTM d’un appareil il possible de calculer exactement à quoi ressemblera le signal de sortie. La FTP, relative à la phase, introduit une légère asymétrie dans les courbes, généralement négligeable (fig.12 et 13).

Fig. 12 – Allure typique de la FTO
NB : seul le transfert de modulation FTM est significatif, le transfert de phase FTP a peu d’effet et peut être négligé

Fig. 13 - DÉGRADATION D’UNE IMAGE LORS DU TRANSFERT

Si plusieurs appareils sont disposés en série (en cascade), leurs FTM se multiplient (sauf pour les groupes de lentilles… car il arrive qu’une lentille corrige l’erreur d’une autre lentille) alors que leurs FTP s’additionnent. La FTM de la plupart des appareils peut être calculée a priori à partir des données fondamentales du projet : on peut donc calculer à l’avance un appareil complexe pour atteindre un résultat donné.

Des difficultés théoriques se présentent pour les systèmes à laser et pour les réseaux de fibres optiques, mais des parades ont été trouvées.

La FTO est une caractéristique tout à fait objective, et l’équipement pour sa mesure existe.

5. Le bruit

Tout appareil est affecté d’un bruit, supposé blanc (c.à.d. aléatoire). Son seuil de détection doit donc être supérieur au bruit, sous peine d’enregistrer beaucoup de fausses détections. C’est une limite de principe, qu’on ne peut supprimer mais qu’on peut améliorer par diverses astuces.

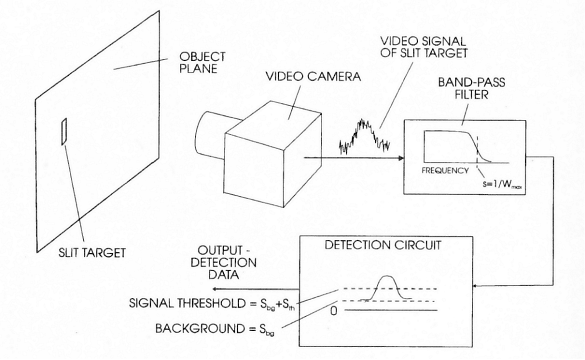
Par exemple si la cible est une fente, son image couvrira plusieurs lignes d’une vidéocaméra. On peut alors sommer les indications de ces lignes (p.ex. M lignes). De ce fait le signal sera multiplié par M mais le bruit seulement par √M, car c’est un bruit aléatoire, dit Root Mean Square.

On peut aussi faire passer le signal de sortie de la vidéocaméra, qui est très affecté par le bruit, à travers un filtre passe-bande dont la fréquence de coupure sera soigneusement calculée pour être très inférieure à celle du spectre de puissance du bruit. Ceci est rendu explicite sur la fig.14 dans le cas d’une fente. Le signal sortant sera légèrement affaibli mais bien « nettoyé » de son bruit.

Fig. 14 - SUPPRESSION (partielle…) DU BRUIT PAR UN FILTRE PASSE-BANDE

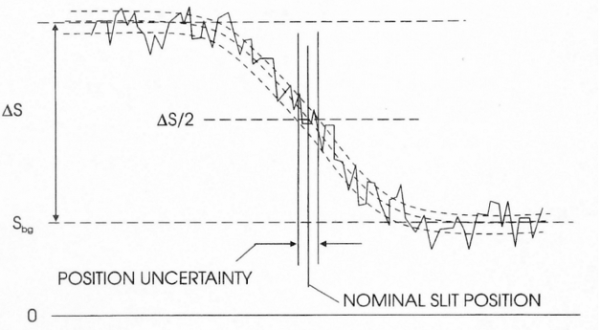
Dans le cas d’un bord vertical abrupt le signal ne sera plus une courbe à maximum mais une sigmoïde (fig.15). On voit que le bruit se traduit par une incertitude sur la position du bord.

Qu’on réduise ou non ces incertitudes, il faut les connaître. Ce sont des marges d’erreur inévitables, et qui deviennent proportionnellement plus importantes lorsque le signal est faible : c’est l’effet incompressible de la diffraction (v. plus haut).

Fig. 15 - EFFET DU BRUIT SUR L’INCERTITUDE DE LA POSITION D’UNE FENTE

6. L’œil

6.1 Ses caractéristiques neurophysiologiques

On peut demander à l’œil (donc ultimement au cerveau) de juger une image. Mais il faut bien distinguer deux types de tâches : apprécier des seuils de discrimination à partir de cibles, comme par un appareil, ou porter un jugement « esthétique ». Les modèles actuels pour ces tâches restent incomplets et empiriques.

Le diamètre de la pupille varie environ de 3 à 8 mm selon la luminance du champ. Elle commence à se contracter lorsque la luminance dépasse ± 1 candela/m² et la contraction devient maximale pour 1000 candelas/m².

L’angle de vision est très grand et dépasse 70° du côté nasal et 100° du côté temporal. Il est cependant de 1,4° seulement dans la zone fovéale, où la vision est la plus précise. C’est donc dans cette région que sont pratiqués les tests.

Les cellules réceptrices (qui ont, ne l’oublions pas, un rendement quantique) sont très concentrées autour de l’axe de vision. Les cônes, responsables de la vision colorée (dite photopique), présentent un maximum très pointu de ± 140.000/mm² dans l’axe de vision. Les bâtonnets, responsables de la vision crépusculaire (dite scotopique) présentent eux un maximum de ± 150.000/mm² sur un cercle de 20° autour de l’axe de vision. La vision crépusculaire est monochromatique (plus ou moins bleue) et prend le relais lorsque la luminance tombe au-dessous de 0,002 candela/m². Les cônes par contre sont de 3 types, répondant respectivement (et approximativement) au bleu, au vert et au rouge.

6.2 Ses imperfections

L’œil est un instrument très imparfait si on le compare aux appareils. Il ne présente aucune correction de l’aberration chromatique, qui est à peu près identique chez tous les sujets. Il corrige imparfaitement l’aberration de sphéricité, et de façon variable d’individu à individu. Pour rappel l’aberration de chromaticité résulte de la réfraction différente des rayons selon leur fréquence : il est donc impossible de réaliser sur la rétine une mise au point parfaite pour toutes les couleurs. La focalisation moyenne se fait dans le vert. Un écart d’une dioptrie dans le bleu tombe à zéro pour 600 nm (zone du vert) puis à -0,5 dioptrie pour le rouge. C’est ce phénomène qui fait que certaines couleurs semblent « avancer » et d’autres « reculer ».

6.3 Comparaison avec la machine

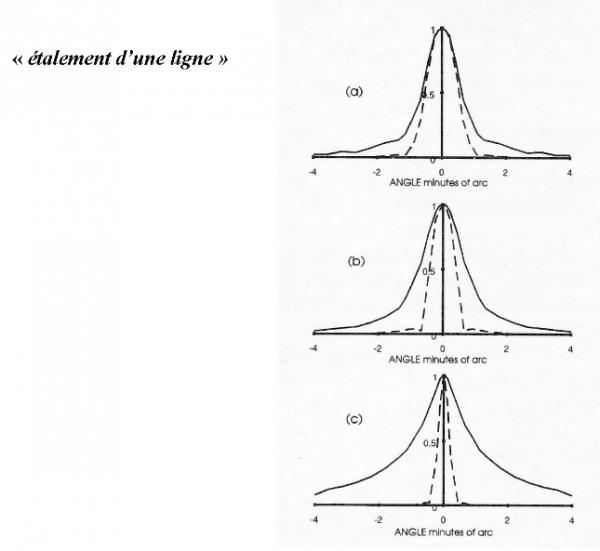
On a comparé le profil produit par l’œil devant une ligne, à celui produit devant la même ligne par une machine optique (limitée bien entendu par la diffraction). Ce profil est appelé fonction d’étalement (fig. 16).

Fig. 16 - COMPARAISON DES PERFORMANCES DE L’ŒIL (trait plein) D’UN APPAREIL (trait tireté) NB : l’angle est celui de la pupille, respectivement ouverte à 2, 3 et 5,8 mm

L’œil se révèle toujours inférieur à la machine, et son défaut s’accroît lorsque le diamètre de la pupille augmente, de 2 à 3 mm puis à 5,8 mm. Les courbes sont « normalisées » en faisant leur pic =1, de façon à permettre la comparaison. La résolution d’une fréquence spatiale de 10 c/° tombe ainsi de 0,55 à 0,25 lorsque la pupille s’ouvre de 2 à 5,8 mm.

Il est difficile d’apprécier l’erreur provoquée par le côté granulaire des arrangements de photorécepteurs, ainsi que celle des processus neuronaux ultérieurs. On dispose toutefois de mesures sur rétine excisée.

Lorsqu’on effectue ces mesures et calculs on trouve que le système nerveux présente une sensibilité maximale, non à 0 cycles/mm, mais vers 30 c/mm (soit pour une largeur de cycle d’environ 0,04 mm) ! La sensibilité décroît au-dessous. Ceci implique que la réponse est maximale (i.e. =1) à l’endroit du stimulus, mais tombe à zéro pour un écart de ± 0,005 mm de part et d’autre, puis devient négative (± -0,1 pour un écart de 0,01 mm), pour redevenir lentement nulle vers 0,05 mm.

Ces observations sont en accord avec l’hypothèse d’un câblage neuronal de plusieurs récepteurs en champs réceptifs, présentant un centre positif et un pourtour inhibiteur. La dimension de ces champs varie bien entendu. Leur zone centrale est très petite : de quelques minutes d’arc seulement dans la fovéa. Vers la périphérie elle augmente et peut atteindre 1°. L’intérêt de ces dispositifs passablement complexes est surtout économique : il permet de réduire le flux d’information émanant de 125.10⁶ de photorécepteurs à 1.10⁶ de neurones dans le nerf optique.

6.4 Les mesures subjectives

Ces mesures revêtent nécessairement un aspect « esthétique » et sont malaisément quantifiables. On présente des images à de nombreux sujets en leur demandant d’apprécier la « différence juste perceptible ». On suppose que leurs jugements forment une distribution normale (au sens du calcul des probabilités). Cette sorte de mesure est affecté par de nombreux facteurs, à commencer par le type d’image : les observateurs se montrent par exemple beaucoup moins exigeants pour les portraits que pour les paysages.

6.5 La reconnaissance d’objets complexes

Les mesures de FTO sont basées sur des figures simples telles que disques, bords, fentes ou réseaux, rares dans la réalité. La réalité par contre est trop complexe, car l’objectif final est de distinguer un cheval d’une vache, ou un char d’une jeep. On a donc recherché une solution intermédiaire, où la machine explore systématiquement le champ selon des tranches horizontales ou barres. Le nombre et l’épaisseur des barres sont évidemment cruciaux pour la performance finale, et on les choisira en fonction du but poursuivi. Par exemple (on ne s’étonnera pas que ces recherches soient surtout menées par les militaires) le repérage d’un half-track (véhicule semi-chenillé) requiert (critères de Johnson) :

• 1 barre pour sa détection simple

• 1,5 barres pour déceler son orientation

• 4 barres pour reconnaître son type

• 5 barres pour l’identifier

Ce domaine est sans doute le seul où la prétendue théorie des prototypes puisse avoir quelque valeur pratique.

6.6 Le rendu des couleurs

Il peut être critique dans certaines applications, mais la perfection est impossible, surtout en raison du choix limité des colorants photographiques et des photophores des TRC. En outre des problèmes latéraux peuvent surgir, dus aux caractéristiques spectrales des revêtements anti-réflexion des lentilles, ou des lampes-sources du système.

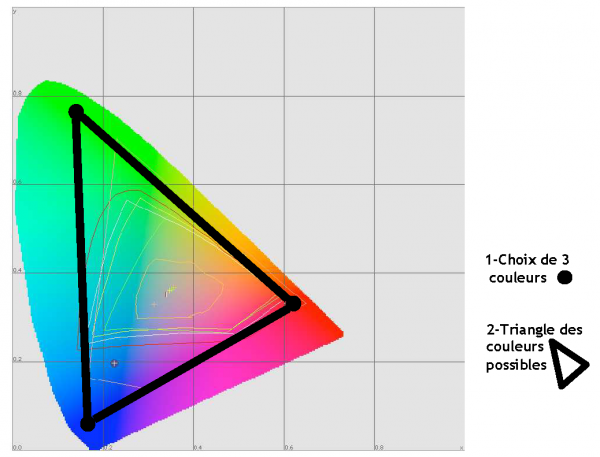
Les sensations colorées sont dues aux réponses des cellules photoréceptrices de la rétine. Les bâtonnets ont un pic de sensibilité situé beaucoup plus bas que le bleu (± 425 nm), ce qui explique pourquoi le soir paraît bleu. Les cônes sont de trois types, sensibles respectivement aux longueurs d’onde courtes (Small), moyennes (Medium) et grandes (Long). C’est erronément qu’on les appelle parfois bleus, verts et rouges. Trois coordonnées suffisent donc pour définir la chromaticité : c’est le système « tristimulus ». Cependant afin de pouvoir la représenter en 2D on a normalisé les valeurs de façon à ce que X + Y + Z = 1. Il reste ainsi un graphique en X/Y sur lequel les couleurs physiquement possibles sont contenues dans une figure en forme de langue (fig. 17).

Fig. 17 – SYSTÈME R-B-V

Plusieurs conséquences importantes sont alors à relever. Si on part de 3 sources colorées, chacune occupe un point de la figure, et le mélange de ces 3 sources ne peut donner qu’un point situé à l’intérieur du triangle formé par les 3 points : toute autre couleur est irréalisable par ce système. D’autre part une même sensation colorée peut être obtenue à partir d’un nombre théoriquement infini de triplets différents : c’est ce qu’on appelle le métamérisme. C’est pourquoi un système générateur d’images n’est fidèle que pour une illumination spécifique.

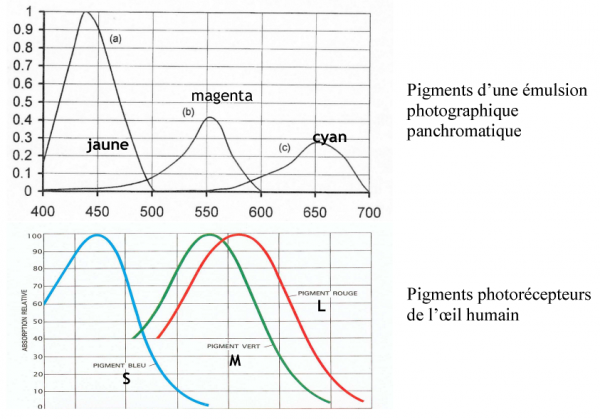
Pour terminer on donnera quelques précisions sur les difficultés que rencontre le rendu technique des couleurs s’il cherche à correspondre au mécanisme neurophysiologique de leur perception. Les fig.18 et 19 permettent de comparer les deux systèmes. Comme il se doit, tous deux sont trichromatiques, mais il s’en faut de beaucoup pour que leurs courbes de sensibilité soient identiques. La FTM permet de quantifier ces écarts et on observe notamment :

• qu’à certaines valeurs de la fréquence spatiale une émulsion photographique dite à grain fin présente des FTM > 1 ;

• que la réponse spectrale d’un film dit panchromatique est très décalée par rapport à la vision humaine : elle présente un creux pour le vert, elle est sensible aux longueurs d’onde < 400 nm donc aux UV, et elle « coupe » le rouge-violet ;

• les films dia sont composés de trois couches transparentes superposées, mais n’ayant pas du tout la même sensibilité : si on chiffre à 1 celle de la couche jaune, la magenta vaut 0,4 et la cyan seulement 0,3. De plus la réponse est une courbe en cloche et non une bande carrée.

Fig.18 - L’ŒIL ET L’APPAREIL PHOTOGRAPHIQUE (longueur d’onde en nanomètres)

De leur côté les sources de lumière interviennent aussi. Elles ont été soigneusement codées en fonction de leur bande d’émission (longueur d’onde λ) et en précisant leur température de couleur (en °K) laquelle varie de 300 à 6000. Plus cette température est élevée plus la lumière est blanche. Celle du soleil est proche de 6000°K, mais les rayons infra-rouges sont fortement absorbés par l’atmosphère.

Il faut signaler pour terminer des études très originales entreprises par Vojko Pogačar (Université de Maribor). Au lieu de qualifier une fois pour toutes la lumière solaire, il en étudie la variation au cours de la journée et au cours des saisons. Il met ainsi en évidence de fortes variations d’intensité et de composition, que l’œil doit compenser pour admettre la stabilité de l’univers qu’il perçoit.

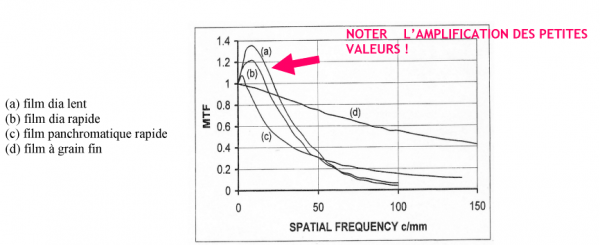
Fig. 19 - FTM DE QUELQUES MATÉRIAUX PHOTOGRAPHIQUES