La face cachée des diagrammes d’Euler

Le succès de la méthode d’Euler tient à l’aide visuelle qu’elle offre lors de la résolution des problèmes logiques. Une attention particulière montre cependant que cette aide n’est obtenue que grâce à une économie graphique, qui sacrifie la rigueur de la méthode à sa clarté.

Euler présente ses diagrammes pour la première fois dans la lettre CII datée du 14 février 1761, après avoir définit les différents types de propositions :

L’idée consiste donc à représenter l’extension de la classe, c’est-à-dire à concevoir l’ensemble de ses individus comme enfermés à l’intérieur d’une cloison circulaire.

La face visible des diagrammes

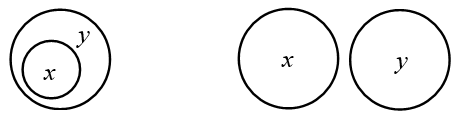
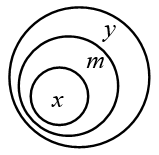
Grâce à cette méthode de représentation des classes, simple et intuitive, Euler représente aisément les différentes propositions logiques entre classes, selon que les cercles s’incluent, s’excluent ou s’entrecroisent. Ainsi suffit-il de représenter un cercle x entièrement inclus dans un cercle y pour représenter la proposition « Tous les x sont y » (figure de gauche), alors que deux cercles entièrement distincts représentent clairement la proposition « Aucun x n’est y » (figure de droite) :

Avec cette méthode de représentation des propositions, Euler s’applique à résoudre des problèmes logiques avec l’usage exclusif de ses diagrammes. Le principe de résolution des syllogismes repose sur deux règles simples qu’énonce Euler comme suit :

Le fondement de toutes ces formes se réduit à ces deux principes sur la nature du contenant & du contenu.

I. Tout ce qui est dans le contenu se trouve aussi dans le contenant &

Examinons par exemple le syllogisme dont les prémisses sont « Tous les x sont m » et « Tous les m sont y », et essayons d’en déterminer la conclusion avec la méthode d’Euler. La représentation de la première prémisse (« Tous les x sont m ») revient simplement à dessiner, comme nous l’avons vu plus haut, un cercle x dans un cercle m (figure de gauche). De la même manière, pour représenter la seconde prémisse (« Tous les m sont y »), il suffit de dessiner un cercle m dans un cercle y (figure de droite) :

Pour résoudre notre problème, il nous faut combiner les deux diagrammes ci-dessus pour entrevoir la relation entre les classes x, m et y sur une seule et même figure. On obtient alors trois cercles correspondant aux trois classes susdites, de sorte que le cercle représentant x soit inclus dans le cercle représentant m qui lui-même est inclus dans le cercle représentant y :

Trouver la conclusion qui découle des prémisses revient à déterminer la relation entre les classes retenues x et y en éliminant le moyen terme m. Pour cela, il suffit d’effacer le cercle représentant la classe m. On obtient alors un cercle représentant x entièrement inclus dans le cercle représentant y :

On voit clairement sur ce diagramme que la conclusion du syllogisme est : « Tous les x sont y ». Nous avons ainsi agi en conformité avec le premier principe d’Euler énonçant que : « Tout ce qui est dans le contenu se trouve aussi dans le contenant ». En effet, sachant que m est contenu dans y, il s’ensuit que x étant dans le contenu m, il se trouve donc aussi dans le contenant y. La force des diagrammes d’Euler est qu’ils dispensent d’apprendre ces principes pour les appliquer, puisqu’avec sa méthode visuelle, la conclusion se retrouve d’elle-même devant nos yeux, sans qu’on n’ait à en déterminer ou comprendre les raisons (que sont justement les deux principes d’Euler). Les diagrammes d’Euler permettraient donc de façon quasi-mécanique de résoudre des syllogismes grâce à une méthode de représentation intuitive et à des règles de manipulation élémentaires. Euler n’en était pas peu fier et vante ainsi les mérites de sa méthode :

La face cachée des diagrammes

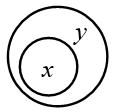
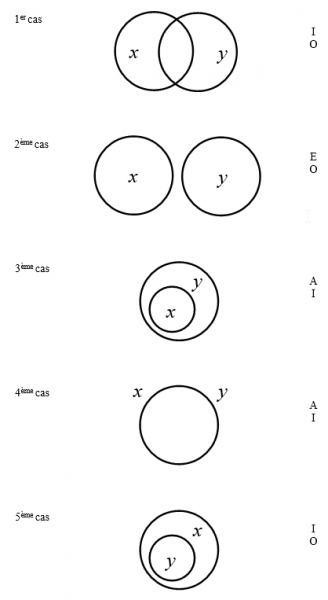
Un regard plus soigné montre cependant que les diagrammes d’Euler souffrent de sérieuses limites, notamment quant à la représentation visuelle des propositions. En effet, on peut observer qu’il y a une certaine ambigüité du rapport que les diagrammes ont aux propositions. Ainsi, une proposition donnée peut en réalité correspondre à plusieurs figures. Il faut par exemple deux figures pour représenter toutes les possibilités qu’offre la proposition « Quelques x sont y », selon que x soit en partie à l’intérieur de y et en partie à l’extérieur de y (figure de gauche), ou que x soit complètement à l’intérieur de y (figure de droite). Dans ces deux cas, on voit bien qu’il y a des x qui sont des y :

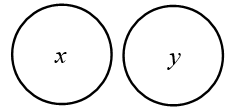
A l’inverse, une même figure peut correspondre à plusieurs propositions. Examinons par exemple la figure ci-dessous, constituée de deux cercles distincts représentant les classes x et y :

On voit clairement dans cette figure qu’il n’y a pas de x qui soient aussi des y, ce qui revient à affirmer la proposition « Aucun x n’est y ». Cependant, on y voit aussi qu’il y a des x qui ne sont pas des y, ce qui correspond à la proposition « Quelques x ne sont pas y ». Pour démêler cette situation, établissons une table des correspondances entre les différentes propositions canoniques de la logique classique et les différentes relations possibles entre deux classes. Nous savons qu’une proposition en logique classique est formée d’un signe de quantité (« Tous », « Aucun », « Quelques »), d’un sujet, d’une copule (« est », « sont ») et d’un prédicat. Toute proposition consiste donc à affirmer ou nier l’attribution d’un prédicat à la totalité ou à une partie d’un sujet. On distingue donc quatre types de propositions, selon qu’elle soit particulière ou universelle, affirmative ou négative :

• La proposition affirmative universelle, dite proposition en A, a la forme « Tous les x sont y ».

• La proposition négative universelle, dite proposition en E, a la forme « Aucun x n’est y ».

• La proposition affirmative particulière, dite proposition en I, a la forme « Quelques x sont y ».

• La proposition négative particulière, dite proposition en O, a la forme « Quelques x ne sont pas y ».

On mesure clairement dans cette table l’ambiguïté dans la correspondance entre les propositions et les figures, contrairement à la présentation « idéalisée » ou « simplifiée » d’Euler. Un diagramme peut donc en cacher un autre, et une proposition peut en cacher une autre.

La rançon de la clarté

En utilisant cette table des correspondances, nous pouvons résoudre les problèmes logiques plus rigoureusement en représentant tous les cas de figures découlant des prémisses, puis en éliminant le cercle correspondant au moyen terme, et en déterminant enfin dans la table des correspondances la (les) proposition(s) correspondant à toutes les combinaisons tolérées entre les termes retenus. Pour illustrer cette méthode, nous allons résoudre le problème discuté plus haut, et qui consiste à trouver la conclusion qui découlent des deux prémisses suivantes : « Tous les x sont m » et « Tous les m sont y ». Commençons par représenter nos deux prémisses, toutes deux propositions en A. Comme l’indique la table des correspondances, chacune se décline sous deux formes différentes suivant les 3^ème et 4^ème cas. Ainsi, la représentation de la première proposition « Tous les x sont m » nécessite les diagrammes [1] et [2] :

De la même manière, la représentation de la seconde proposition « Tous les m son y » nécessite les deux figures [3] et [4] :

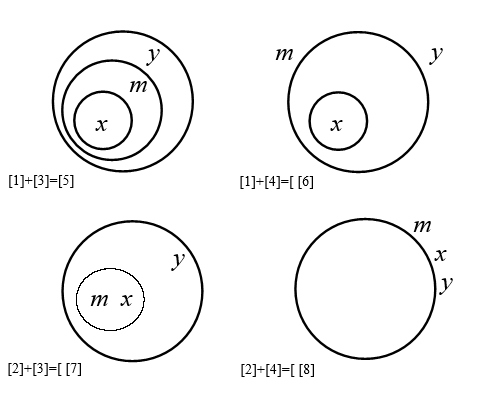
La représentation des deux propositions avec un même diagramme nous amène à superposer chacune des deux figures correspondant à la première avec chacune des deux figures correspondant à la seconde. Nous obtenons quatre diagrammes possibles selon les configurations choisies. Par exemple, en combinant les figures [1] et [3], on obtient le diagramme [5], et ainsi de suite :

On trouve ainsi quatre diagrammes ([5], [6], [7] et [8]) représentant les quatre configurations possibles, déterminées par les deux prémisses du problème, des classes x, y et m. On notera que seul le diagramme [5] est utilisé avec la méthode « simplifiée » d’Euler, expliquée dans la première partie de cet article. Dans un sens, le diagramme [5] « cache » les trois autres diagrammes, pourtant pas moins légitimes, bien qu’ils nous paraissent adhérer moins « naturellement » aux données du problème, à cause de la confusion entre inclusion et inclusion stricte.

Pour résoudre le problème, il nous faut maintenant éliminer le moyen terme m des quatre diagrammes précédents ([5], [6], [7] et [8]) pour trouver la (les) relation(s) possibles entre les termes retenus x et y. Il en résulte deux configurations possibles : en éliminant m des diagrammes [5], [6] et [7], nous obtenons la figure [9], alors qu’en éliminant m du diagramme [8] nous obtenons la figure [10] :

On obtient deux figures ([9] et [10]) relevant respectivement du 3^ème et du 4^ème cas de notre table des correspondances. On peut donc établir la liste des propositions communes aux deux cas : « Tous les x sont y » et « Quelques x sont y », qui constituent les conclusions du problème, la première (« Tous les x sont y ») étant la conclusion complète car elle englobe la seconde.

On le voit, la résolution rigoureuse du problème ne peut faire l’économie de configurations légitimes et nécessaires, pourtant passées sous silence par Euler. C’est que cette rigueur a un prix. Notre méthode est en effet beaucoup plus compliquée, et perd l’avantage visuel de la méthode d’Euler. D’une certaine façon, Euler ne fait que caricaturer avec ses diagrammes les relations logiques que l’on souhaite représenter. En cela, il privilégie la clarté au détriment de la rigueur. L’aide visuelle est à ce prix.