Mathématiques, de l’action à la vision
Mathématiques et action
Une conception naïve et répandue des mathématiques veut que les notions qui ont cours en ce domaine soient engendrées par abstraction et idéalisation à partir de l’observation de la nature. Par exemple : les notions de droite ou de plan seraient induites à partir des portions plus ou moins étendues de ligne ou de plan dont le monde nous offre le spectacle. En réalité, ce processus d’abstraction suppose son résultat déjà acquis pour pouvoir se déployer. Entre le lac et l’idée de plan, c’est la seconde qui se projette sur le premier, non le premier qui engendre la seconde (un signe en est que les paysages maritimes et lacustres sont très répandus sur la terre, mais ne suffisent pas à transformer leurs spectateurs en géomètres) ; de même, il faut déjà pratiquer la numération pour qu’une collection d’objets puisse évoquer un nombre. Par ailleurs, la quantité de notions mathématiques susceptibles d’être mises en rapport visuel avec des éléments du monde environnant est assez réduite, voire très réduite par rapport à l’ensemble de ces notions.
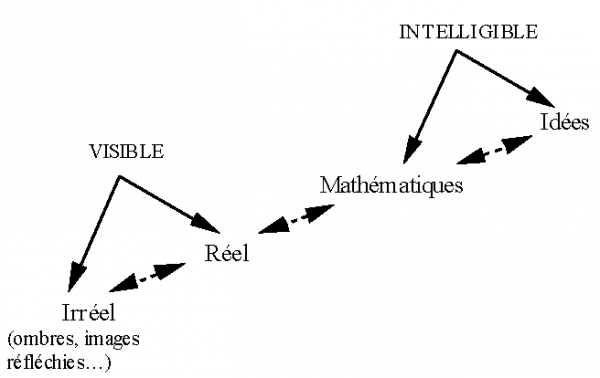
Cette conception des mathématiques comme abstraites du spectacle du monde s’accorde avec les doctrines sensualistes, selon lesquelles les idées ne sont que des sensations transformées, et avec le nominalisme, qui veut que nos concepts ne soient que des étiquettes plus ou moins commodes pour découper et appréhender la réalité. Elle s’oppose aux différentes formes d’innéisme et d’universalisme, et, en particulier, à la conception « platonicienne » des mathématiques. Selon Platon, le monde matériel dont nous faisons l’expérience n’a pas plus de consistance ontologique que des ombres chinoises sur la paroi d’une caverne : ce qui est vraiment, ce sont les Idées, dont tout ce que nous expérimentons par les sens n’est qu’un reflet, sans plus de consistance par rapport à elles que l’image d’un arbre à la surface d’une mare par rapport à l’arbre lui-même. Ce à quoi nous assistons à l’intérieur de la caverne du monde est incapable, en soi, de nous conduire aux Idées. Mais l’âme humaine a, à des degrés divers, recueilli quelque chose de ces Idées avant d’être incarnée sur la terre, et c’est ce savoir enfoui, atteint par la réminiscence, qui permet de saisir le sensible comme il convient. Quant à l’opérateur de projection des Idées sur le monde ambiant, qui permet, en retour, de reconduire le monde ambiant vers les Idées, ce sont les mathématiques.
Pour essayer de mieux saisir ce qui conduit Platon à faire jouer aux mathématiques un rôle aussi exorbitant, il est utile de se rappeler la façon dont les Grecs, autant que nous puissions en juger, ont été conduits aux mathématiques. Ni en scrutant leur âme, ni en contemplant le monde, mais en s’interrogeant et en réfléchissant sur ce que c’est qu’apprendre, sur l’acte d’apprendre en lui-même (la mathesis est d’abord un apprendre, avant que son sens ne se spécialise avec ce qu’on appelle les mathématiques). Que découvrirent-ils ? Entre autres, que nulle connaissance n’est possible qui ne soit, en partie au moins, une reconnaissance ; qu’un certain savoir doit toujours précéder l’apprendre pour qu’un apprendre soit concevable. Ce qui est déjà là, en tant qu’il permet l’appréhension de ce qui est à connaître, n’est autre, pour parler en termes modernes, qu’un cadre transcendantal : non pas ce qui est directement expérimenté, mais la structure qui permet l’expérience et dans laquelle elle s’inscrit. Pour le pythagorisme, comme pour le platonisme qui, sur ce point, en est l’héritier, ce cadre transcendantal est mathématique. Les mathématiques sont toujours déjà là, antérieures à toute expérience sensible, qui ignore leur présence mais leur doit d’être elle-même présentifiée. Il en résulte que ce n’est pas de l’expérience mondaine en tant que telle que sont à même d’apparaître les mathématiques mais, en quelque sorte, d’un pli de cette expérience sur elle-même, quand, au lieu d’être tournée vers l’objet d’expérience, elle évacue cet objet et se retourne vers sa propre structure.
- Note de bas de page 1 :
-
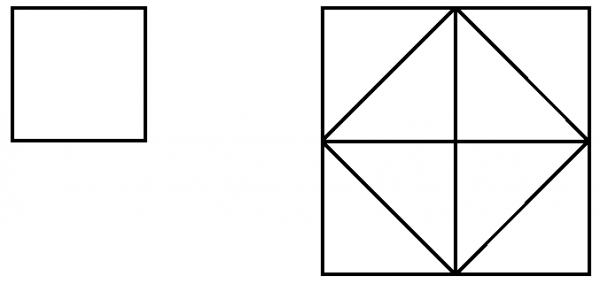
Cette construction fournit la démonstration du théorème de Pythagore, a2+b2=c2 quand a, b, c mesurent les côtés d’un triangle rectangle, a et b les côtés adjacents à l’angle droit, c l’hypoténuse, dans le cas particulier a=b ; le cas général s’obtient par une légère adaptation de l’argument.
Pour montrer que le savoir géométrique n’est pas un savoir qui s’acquiert, mais un savoir qui est déjà là, et dont il s’agit de se ressaisir dans la réminiscence, Socrate entreprend dans le Ménon de montrer qu’un jeune esclave sans instruction est un géomètre qui s’ignore. À cette fin, il lui fait (re)trouver, par ses questions et le dessin, la solution du problème de la duplication du carré (c’est-à-dire : étant donné un carré, construire un carré d’aire double au premier). La démarche consiste à juxtaposer quatre exemplaires du carré initial, d’aire A, de manière à former un grand carré, d’aire 4A ; en divisant chacun des petits carrés par une diagonale qui joint les milieux des côtés consécutifs du grand carré, on construit un carré central dont l’aire est égale à quatre fois la demi-aire des petits carrés, c’est-à-dire 4×(A /2) = 2A, le double de l’aire du carré initial1.
Qu’est-ce qui a provoqué la « réminiscence » ? Non pas une méditation introspective, mais l’évidence se dégageant des figures successivement tracées au sol par Socrate. Plutôt que de conclure, comme dans le dialogue de Platon, que la démonstration fait découvrir quelque chose que le jeune esclave savait déjà, il est possible d’imaginer que ce savoir est l’œuvre même de la démonstration. Nous n’entendons pas entrer, ici, dans le débat sur le statut d’existence des idéalités mathématiques, et la part qui revient à l’activité du mathématicien vis-à-vis d’elles, entre dévoilement et constitution. Notre propos est uniquement de souligner que l’interprétation des réponses de l’esclave en termes de réminiscence n’a rien d’inévitable, et que l’on peut tout aussi bien considérer que la démonstration, au lieu de révéler un savoir déjà là, le constitue.
- Note de bas de page 2 :
-
Bourbaki, Théorie des ensembles, Paris, Hermann, 1970, Introduction E I.7.
- Note de bas de page 3 :
-
« Lorsqu’on dit que le dialogue est profondément impliqué au cœur des mathématiques, il ne faut donc pas oublier qu’il s’agit là d’une forme extrêmement particulière. Ce n’est pas le dialogue ordinaire, comme on le croit souvent, c’est un autre dialogue tel que le “il”, ordinairement exclu, soit inclus dans l’interlocution. Si le “il” rentre dans l’interlocution, on s’aperçoit par contrecoup que celui qui en est expulsé est le “tu”. Le fameux tiers exclu, qui caractérise la logique binaire du même nom, c’est le “tu”. Ce tiers expulsé, c’est l’instance complaisante qui renvoyait indéfiniment la balle en échangeant sa position avec celle du “je” » (Dany-Robert Dufour, Les Mystères de la trinité, Gallimard, coll. Bibl. des sciences humaines, 1990, p. 394). L’instance objectante de l’autre est bien entendu susceptible d’être intériorisée. Evert Beth écrit : « Une certaine culture mathématique et un certain entraînement permettront au mathématicien d’anticiper, dans une certaine mesure, les “contre-exemples” que son adversaire pourrait utiliser. […] Notons que la structure d’une telle anticipation est transférée du niveau de la discussion à celui d’un raisonnement formel. Si l’on introduit un raisonnement déductif par les mots : “Soit ABC un triangle quelconque” ou : “Soit ABC un triangle arbitraire”, c’est, pour ainsi dire, qu’on laisse le choix de ce triangle à un opposant imaginaire » (Evert W. Beth et Jean Piaget, Épistémologie mathématique et psychologie – essai sur les relations entre la logique formelle et la pensée réelle, PUF, coll. Bibl. scientifique internationale, 1961, p. 11).
Mathématiques implique démonstration. « Depuis les Grecs, qui dit mathématique dit démonstration ; certains doutent même qu’il se trouve, en dehors des mathématiques, des démonstrations au sens précis et rigoureux que ce mot a reçu des Grecs »2. C’est au point qu’on pourrait définir les mathématiques ainsi : comme le domaine où ont cours les démonstrations. Une démonstration a ceci de particulier qu’elle appelle l’assentiment par un enchaînement d’arguments qui s’impose à tout esprit disposé à faire l’effort de le suivre. De là une grande partie de la séduction exercée sur Platon : dans une cité athénienne déchirée par les conflits internes, où les discours entretenaient et envenimaient la discorde au sein du peuple au lieu de le réconcilier, se montraient incapables de rétablir la concorde, les propositions mathématiques avaient cette merveilleuse propriété d’être soustraites à la controverse, d’obliger les esprits sans qu’il soit nécessaire de recourir à la force, ni à l’autorité, ni à la persuasion. Celui qui élabore une démonstration s’adresse à un autre, présent ou non, réel ou fictif, mais à un autre particulier : un autre en qui n’est supposé, pour juger des arguments présentés, aucune sympathie, aucune connivence3. À cet égard, le développement de la rigueur démonstrative doit certainement beaucoup à l’esprit agonal des Grecs. Cela étant, cette rigueur ne peut s’exercer pleinement que sur un certain terrain. Alors que toute monstration est monstration de quelque chose, la démonstration est monstration d’elle-même : quand on pointe l’index dans une certaine direction, le sens est d’inviter à regarder de ce côté ; quand Socrate divise un carré en deux par la diagonale, le sens de son geste au sein de la démonstration est de diviser le carré en deux par la diagonale. Voilà pourquoi la démonstration force l’assentiment : il n’y a pas de distance entre la monstration et ce qui est montré. Mais la démonstration ne peut se déployer que si les objets et notions qu’elle fait intervenir ont ce même caractère de se montrer eux-mêmes entièrement – ce qui délimite exactement le domaine des mathématiques. Un objet concret, tangible, tel un rocher, a une réalité que la définition en tant que « masse de matière minérale dure » ne capte qu’en partie. L’ajout de caractéristiques supplémentaires comme la masse, les dimensions, la couleur, la composition chimique, la résistance à l’écrasement, au cisaillement, etc. ne parviendra jamais à épuiser cette réalité. Un cercle de rayon R, en revanche, n’est rien d’autre que l’ensemble des points d’un plan dont la distance à un point donné est R. La coïncidence de l’objet avec sa définition est possible dans la mesure où l’objet et sa saisie ne font qu’un – dans la mesure, donc, où la définition est purement fonctionnelle. Les mathématiques ne procèdent ni du sujet explorant les replis de son âme (la définition mathématique du cercle ne jaillit pas de l’introspection), ni des objets matériels idéalisés (elle ne jaillit pas davantage des formes plus ou moins circulaires présentes dans la nature), mais de l’action en direction de l’objet (délimiter une aire circulaire), quand action et objet parviennent à s’identifier dans une définition fonctionnelle. L’action, repliée sur elle-même, révèle sa structure, devient schème opératoire.
- Note de bas de page 4 :
-
Voir La Valeur de la science (1905), Paris, Flammarion, coll. Champs, 1999, I, chap. III, §5.
Poincaré fait remarquer que pour un être immobile, il n’y aurait pas d’espace, pas de géométrie4. L’espace, avant que s’y déploient nos actions, est engendré par elles. Et c’est lorsque de ces actions considérées en elles-mêmes, intransitivement, se dégagent des structures opératoires, que l’espace devient mathématique – topologique, quand il s’agit d’intérieur, d’extérieur, de frontière, de voisinage, de limite, géométrique quand il s’agit de mesures de longueur, d’angle, de courbure, etc. Les variétés, ces nouveaux types d’espaces apparus en mathématiques à partir du XIXe siècle (Mannigfaltigkeit en allemand, manifold en anglais), concevables à partir du moment où étaient dissociés un substrat topologique, support de différentes géométries possibles, et la structure géométrique proprement dite, peuvent à bon droit être renommés dans certains ouvrages espaces de configuration : appellation qui a le mérite de faire entendre que l’espace n’est pas un contenant universel totalement indépendant des objets qu’il contient et des phénomènes qui s’y produisent, mais toujours l’ensemble des lieux qu’un certain système est susceptible de visiter.
- Note de bas de page 5 :
-
Pour le dire en termes contemporains : ce n’est parce que l’on ne bouge pas que les neurones relatifs au mouvement ne sont pas activés : il y a seulement inhibition des influx moteurs – comme c’est le cas, par exemple, dans le rêve.
- Note de bas de page 6 :
-
La Valeur de la science, op. cit., I, chap. I, §1.
- Note de bas de page 7 :
-
Il en va de même dans tous les domaines des mathématiques. À propos de l’arithmétique, Piaget écrit : « Que l’expérience soit psychologiquement indispensable à la construction du nombre ne prouve nullement que celui-ci soit extrait des objets, sous une forme ou sous une autre. […] En d’autres termes, un sujet agissant de façon empirique peut utiliser les objets à titre de simples supports ou d’occasions de l’action, mais expérimenter en réalité sur lui-même, c’est-à-dire sur la coordination de ses propres actions plus que sur les objets sur lesquels elles s’appuient » (Introduction à l’épistémologie génétique, I. La Pensée mathématiques, PUF, 1950, p. 132). « La logique et le nombre sont dus aux coordinations des actions comme telles du sujet, et ne sont pas extraites de l’objet, quand bien même ce n’est qu’à l’occasion des actions sur les objets que ces coordinations se manifestent » (id., p. 261). Pour compter il faut opérer sur des objets. Mais la notion mathématique de nombre ne peut se former que lorsque les objets se résorbent en tant que tels pour ne plus être que de purs supports de l’action de compter, l’attention se portant intransitivement sur ce que c’est que compter, sur les schèmes opératoires du comptage.
Certes, les mathématiciens n’ont pas besoin de se mouvoir pour faire de la géométrie. Mais si le géomètre peut rester immobile, c’est que l’expérience l’autorise à se mouvoir sur le mode virtuel5. Encore ne reste-t-il pas toujours si hiératique. Poincaré remarquait qu’un mathématicien à l’esprit géométrique, dans ses explications, « est toujours en action, tantôt il semble aux prises avec quelque ennemi extérieur, tantôt il dessine d’un geste de la main les figures qu’il étudie. Évidemment, il voit et il cherche à peindre, c’est pour cela qu’il appelle le geste à son secours »6. Cette attitude justement observée invite à comprendre que l’expérience fondamentale en géométrie ne tient pas à la « vision » de figures, mais à leur tracé. D’où s’ensuit l’embarras des explications une fois que la figure est là, sur le tableau : le moment décisif est passé. Certains font alors des gestes de la main pour reproduire, dans l’air, l’expérience du tracé, d’autres se censurent moins et repassent sans cesse la craie sur la même figure, jusqu’à ce que les traits soient si épais que la figure devient illisible. La première attitude semblerait relever d’un réalisme « platonicien », la seconde d’un réalisme « physicien ». En fait, au-delà de leur opposition apparente, elles traduisent le même phénomène : à savoir les limites d’une identification des « actions » géométriques avec leurs résultats pris pour objets. Et cela, même si l’expérience géométrique ne réside pas dans le fait de tracer, mais à l’occasion de cette action7.
- Note de bas de page 8 :
-
C’est cette caractéristique qui conduit René Thom à écrire : « Je pense que les concepts que l’on peut considérer comme scientifiques sont justement ceux pour lesquels il est possible de donner une traduction univoque dans toutes les langues du monde et que c’est possible, à mon avis, parce qu’on peut spécifier leur signification par référence à des transformations qui peuvent être considérées comme des transformations spatiales » (Paraboles et Catastrophes (Parabole e Catastrofi, 1980), Paris, Flammarion, coll. Champs, 1983, p. 121).
Procédant de l’action, les idéalités mathématiques ne sont pas consignables telles quelles dans l’étant. Pour s’inscrire elles ont besoin d’un système symbolique propre. L’absence, à l’origine, d’un tel système, aurait dû toujours empêcher le développement des mathématiques, confinées à des expériences de pensée individuelles et fugitives, à des illuminations isolées et sans suite – inchoatives faute d’un marquage des étapes antérieures, incommunicables durablement faute de ce même marquage. Mais il y eut la géométrie plane, où un système symbolique est pour ainsi dire donné d’emblée, parce qu’il y a homogénéité, caractéristique de ce que l’on nomme « espace », des opérations auxquelles on y procède, et de leurs résultats constatables8. Le propre de l’opération spatiale, c’est de se montrer elle-même dans son résultat, de sorte qu’on peut oublier la différence entre la figure et ce qu’en vérité elle désigne, c’est-à-dire les opérations ayant présidé à son tracé – entre le carré tracé et tracer un carré. S’il y a une différence, la relation entre les deux termes est parfaitement déterminée, rigide et univoque, canonique, permettant sans conséquences l’identification. (Cela n’est pas vrai par exemple de l’action de compter : n’étant pas une opération spatiale, elle ne se projette pas canoniquement dans l’espace – le nombre deux n’est pas homogène à deux objets. Il y a un espace physique, mais pas de logique ou de nombres physiques).
L’identification spontanée entre l’opération spatiale et son résultat, la notion géométrique et une figure idéale à laquelle les figures réelles peuvent servir de symbole, est ce qui a permis, en l’absence de langage formalisé, la naissance de la géométrie mathématique. C’est aussi ce qui a trompé sur son essence. Platon – qui certes n’était pas à titre personnel un très bon mathématicien – croyait toujours avoir affaire, au bout du compte, à une « vision ». Faute d’un langage symbolique approprié la figure idéale, dont les figures réelles étaient l’évocation, demeurait le référent ultime – et c’est sans doute l’une des raisons qui empêchèrent les Grecs de tirer tout le parti possible de la nature opératoire des concepts mathématiques. C’est à l’Europe moderne que cette tâche revint, à partir de Descartes qui, grâce à l’algèbre, put rendre virtuelle la figure par une équation. Pour écrire une équation cependant, un langage symbolique était nécessaire, dont l’élaboration ne fut pas le moindre enjeu des travaux mathématiques des XVIIe et XVIIIe siècles. Remarquons que cette élaboration n’était possible que dans une culture de l’écrit, ce qui n’était pas le cas dans la Grèce antique où la plus haute dignité restait à la parole. Peut-être même une culture de l’écrit imprimé était-elle nécessaire, où le signe manuscrit devient imitation du signe imprimé, toujours reproduit à l’identique, qui le stabilise et l’objective. Si aujourd’hui les étapes qui ont marqué la mise au point d’une écriture formalisée peuvent sembler anecdotiques dans l’histoire des mathématiques, elles représentent en réalité un aspect décisif de cette histoire. Outre les facilités d’emploi qu’une telle écriture offre, et les opérations de l’esprit qu’elle simplifie, elle est le seul moyen de consacrer l’indépendance de l’être mathématique par rapport à l’étant, tout en permettant de capitaliser un acquis et en préservant les conditions d’un accord intersubjectif.
- Note de bas de page 9 :
-
De là l’importance particulière, parallèlement aux publications, des conférences, groupes de travail, séminaires. De là également le côté désastreux d’une substitution des présentations par projection (Powerpoint) aux exposés traditionnels, où le mathématicien doit penser à nouveau ce qu’il cherche à expliquer et à écrire au tableau.
Là où Platon marquait une opposition, entre le logos et l’écrit, entre l’intuition vive de l’idée dans la pensée, l’expérience du vrai dans la présence, et son abolition dans les signes duplicables indépendamment de toute pensée, Husserl a identifié une tension. D’une part, l’idéalité géométrique (et, plus généralement, l’idéalité mathématique) a absolument besoin de l’expression linguistique écrite pour que son objectivité soit constituée, indépendamment des activations et des communications immédiates ; d’autre part, l’écrit porte toujours avec lui un risque : permettre une transmission purement formelle, une sédimentation des acquis dont le sens s’évapore pour laisser place à un fonctionnement qui, aussi efficace soit-il, a perdu ses ancrages dans la Lebenswelt. De ce fait, même si l’écrit permet les communications sans allocution directe, l’enseignement et la discussion de personne à personne – avec l’engagement des corps qu’il implique – demeure essentiel, en mathématiques plus encore que dans n’importe quelle discipline de la pensée9.
Mathématiques et vision
- Note de bas de page 10 :
-
La Géométrie (1637) Livre II, A.T. VI, p. 316.
Paradoxalement la géométrie, vouée à l’étude et au déploiement des opérations spatiales, a contribué à tenir caché le caractère fondamentalement opératoire des notions mathématiques. Cela, parce qu’on peut voir des figures géométriques, c’est-à-dire y accéder sans agir. Plus exactement, on a l’impression de pouvoir y accéder sans agir : on peut oublier, une fois la figure tracée, que l’expérience déterminante tient non pas à l’observation de la figure, mais aux principes qui ont présidé à sa construction. Dans le Phèdre de Platon, le seul rôle positif accordé à l’écriture est d’ordre mnémotechnique – elle est là pour aider à se ressouvenir de ce qui est déjà su. De façon analogue, les constructions géométriques ne seraient pas la matière même de la géométrie, mais ce qui permettrait de reconduire à la contemplation de la vérité. Une question, toutefois, se pose : pourquoi les géomètres grecs voyaient-il des cercles, des triangles et des carrés, plutôt que d’autres figures ? Parce que, sans doute, ces formes sont plus simples. Mais en quoi sont-elles plus simples ? En ce que leur procédé de construction est transparent à la vision, en ce que de leur vision on infère la possibilité de les reproduire. C’est cela qui les rend directement intelligibles. Autrement dit la contemplation, qui phénoménologiquement s’oppose à l’action, est cependant, en mathématiques, fondamentalement liée à l’action puisque, en définitive, c’est un ensemble d’opérations que l’on contemple. Au demeurant, les mathématiques grecques étaient authentiquement constructives : Euclide, dans ses Éléments, indique toujours comment tracer les figures – au point que celles-ci purent être omises des éditions anciennes. C’est en vertu de cet aspect constructif que les Éléments ont fourni à Archimède le cadre adéquat pour sa formulation des lois de la statique et, beaucoup plus tard, un modèle dont Lagrange a pu à juste titre se réclamer pour écrire la Mécanique analytique, où domine le principe des mouvements virtuels. Par ailleurs, il est remarquable que, lorsque Descartes définira les courbes susceptibles d’être étudiées par la géométrie, il le fera en se référant explicitement à la méthode qui préside à leur construction : « considérant la Géométrie comme une science, qui enseigne généralement à connaître les mesures de tous les corps, on n’en doit pas plutôt exclure les lignes les plus composées que les plus simples, pourvu qu’on les puisse imaginer être décrites par un mouvement continu ou par plusieurs qui s’entresuivent et dont les derniers soient entièrement réglés par ceux qui les précèdent »10. Ce qui fait la mathématicité d’une courbe est qu’on dispose pour la construire d’un procédé univoque.
- Note de bas de page 11 :
-
Jan Patocka, Qu’est-ce que la phénoménologie ? Grenoble, Jérôme Millon, 1988, p. 73.
- Note de bas de page 12 :
-
Ce fait indubitable n’est pas pour autant immédiatement pris en compte. Un signe en est qu’il a fallu attendre la Relativité pour qu’il soit véritablement intégré aux théories physiques modernes.
- Note de bas de page 13 :
-
On peut rappeler, à cet égard, le problème posé au XVIIe siècle par Molyneux et qui a passionné l’Europe intellectuelle : est-ce qu’un aveugle de naissance, qui a appris à reconnaître en les maniant une sphère et un cube de tailles comparables, serait à même, à supposer qu’il soit subitement guéri de sa cécité, d’identifier sans les toucher la sphère et le cube ? Le débat s’est développé et poursuivi dans la mesure où aucune expérience directe ne venait le trancher. Récemment cependant, la chirurgie a permis de donner à plusieurs enfants, âgés de cinq à dix-sept ans, et atteints de cécité congénitale, un plein usage de la vue. La vision fut d’emblée assez bonne pour permettre la distinction de formes que les enfants avaient préalablement appris à connaître par le toucher. La réponse à la question de Molyneux a été négative : les nouveaux voyants n’étaient pas capables d’établir un rapport entre représentations visuelles et représentations tactiles. En revanche, au bout d’une semaine, le rapport s’était établi. (Voir l’article de Richard Held et al., « The newly sighted fail to match seen with felt », Nature Neuroscience, 14-5, 2011, p. 551-553.)
- Note de bas de page 14 :
-
« Des sens en général », chap. 8 de l’Histoire naturelle de l’homme, Paris, Gallimard, coll. Folio, 1984, p. 113.
Les idéalités mathématiques sont des idéalités opératoires. Cependant, en tant qu’idéalités, elles sont constituées objectivement et, dans cette mesure, peuvent être appréhendées sur le mode de la vision. D’un point de vue phénoménologique, « le contact tactile est pour nous une manière de nous emparer des choses. La présence visuelle, en revanche, est comme un don qui n’exige ni lutte ni effort, qui est simplement là »11. La vision présente le monde comme si nous n’y étions pas – à travers la vision le monde se donne à nous sans que nous ayons à y être ni à interagir avec lui. En fait, un peu de réflexion suffit à montrer que tel n’est pas le cas : nous ne voyons qu’en tant que nous sommes immergés dans le monde, situés en lui12 ; et la perception visuelle est action : l’œil accommode, suit des contours, d’infimes déplacements des yeux et de la tête permettent d’apprécier mouvements et distances. En lien avec la proprioception, la vue permet à une certaine représentation du monde extérieur de s’élaborer. Mais cette représentation demande à être articulée à la représentation qui s’élabore à partir de l’appareil sensori-moteur, et cette articulation s’effectue sous l’autorité du sensori-moteur13. Comme l’écrivait Buffon : « C’est par le toucher seul que nous pouvons acquérir des connaissances complètes et réelles. C’est ce sens qui rectifie tous les autres sens dont les effets ne seraient que des illusions et ne produiraient que des erreurs dans notre esprit si le toucher ne nous apprenait à juger »14. Quitte à comprendre, comme il ressort d’autres passages du même auteur, le toucher comme métonymie de l’ensemble des rapports moteurs et tactiles avec le monde. Par les corrélations qui s’établissent au cours de l’expérience entre motricité et impressions visuelles, la vue peut devenir à sa manière préhension, contact transféré du corps ou de la main à l’œil par la médiation de la lumière.
- Note de bas de page 15 :
-
Les mathématiques sont bien plus qu’une langue pour les sciences modernes de la nature, elles sont un mode d’appréhension du réel. En physique en particulier les mathématiques ne s’appliquent pas, elles s’impliquent, selon l’heureuse expression de Jean-Marc Lévy-Leblond.
La science moderne, tant par la place centrale qu’y occupent les mathématiques15 qu’à travers l’autorité accordée non pas à l’expérience, mais à l’expérimentation, répond parfaitement à la phrase de Buffon citée plus haut : la connaissance recherchée ne se contente pas de la vue, elle exige un contrôle opératoire. (Emblématique est à cet égard Descartes qui, au sein de sa physique, n’admettait que les effets de contiguïté et de chocs.) Cependant, cette connaissance a pour idéal de retrouver quelque chose qui phénoménologiquement s’apparente à la vision. La contemplation s’ouvre à l’immédiate présence, mais ne sait pas pourquoi les choses sont ce qu’elles sont, pourquoi elles se produisent de la façon dont elles se produisent. Poursuivre un tel savoir impose de rompre avec l’immédiate présence. L’espoir peut néanmoins être nourri de retrouver cette présence au bout du compte, au sein d’une vision à laquelle tout est devenu transparent, où tout s’offre au regard selon son mode de production. Les choses, telles qu’elles se donnent initialement, se trouvent patiemment décomposées et recomposées suivant des schèmes opératoires ; mais l’idéal est de renouer, au terme du processus, avec une forme d’évidence.
Une telle ambition n’est pas aussi utopique qu’il pourrait paraître de prime abord. Il était à craindre, par exemple, qu’en s’éloignant des représentations concrètes, les mathématiques finissent par s’égarer et devenir stériles. C’était oublier qu’intuition et évidences, loin d’être des invariants de la pensée, sont relatives à une certaine structuration de cette pensée, et donc aptes à « suivre » les mathématiques au gré de leurs développements. À chaque étape se reconstitue le clivage entre « raison constituée », fonctionnant selon les évidences acquises, et « raison constituante » qui, guidée par l’intuition, travaille à cette acquisition. Voilà pourquoi la fécondité des mathématiques, lorsque celles-ci se sont séparées de l’intuition sensible immédiate, n’a pas diminuée mais s’est maintenue et même accrue, dans des proportions considérables.
Le développement des mathématiques s’effectue selon deux directions : d’une part, l’étude du monde engendré par les notions disponibles et l’élaboration, à partir d’elles, de nouvelles notions, de l’autre, une redéfinition de ces notions à partir de principes plus fondamentaux. À ce double mouvement, correspond une perpétuelle décomposition et recomposition de la vision mathématique. Plus généralement la science moderne, qui avec Galilée s’est donnée pour programme de déchiffrer le monde au travers des mathématiques, ne cesse de décomposer la vision spontanée du monde (déjà liée, dans une large mesure, à nos actions dans le monde, virtualisées), dans le projet de conduire à une nouvelle vision, à une « hyper-vision » réalisant la fusion des différents modes de représentation, combinant la connaissance des modes de production des phénomènes avec l’évidence phénoménologique propre à la vue.