Generazione e visualizzazione delle forme nello spazio: proprietà topologiche e percezione di superfici geometriche
Dans cet article, nous étudions quelques aspects de la visualisation topologique en tant que méthode pour appréhender des propriétés mathématiques et phénoménologiques de l’espace ambiant, dans lequel se constituent nos perceptions et se construit notre rapport au monde. Nous montrons que des opérations apparemment « élémentaires » comme couper et coller peuvent être composées de sorte à donner lieu à des constructions plus complexes, telles que somme connexe et surface à bord, faisant apparaître de nouvelles propriétés. Celles-ci sont de deux types : objectal et holiste ; alors que les premières sont relatives à la structure in se d’un objet géométrique (surface, variété), les secondes concernent surtout les relations entre ce même objet et l’espace dans lequel il est plongé ou immergé. Le premier type de propriétés est mis en évidence par la classe des déformations (ou transformations) appelée homéomorphismes, tandis que le second type de propriétés apparaît clairement grâce à la classe des isotopies. Le point essentiel est que topologiquement deux objets peuvent avoir la même « forme » même si leurs images graphiques nous apparaissent très différentes. Ce qui montre que l’équivalence des formes a un sens topologique beaucoup plus important que l’équivalence entre images. En effet, deux objets peuvent nous apparaître très différents quant à leur présentation graphique et pourtant appartenir à la même famille de formes. Prenons le cas de deux objets dont l’un est noué et l’autre ne l’est pas, alors qu’ils ont une apparence très similaire. Le fait d’être noué ou dénoué est ainsi une propriété de nature topologique qui concerne moins les objets in se, que l’espace tridimensionnel dans lequel ils sont plongés. Étudier les objets et leurs environnements spatiaux revient à essayer de comprendre les dynamiques de transformation et l’émergence de nouvelles propriétés et qualités de ces mêmes objets.
The knot or link as an embedding in three-dimensional space is a whole topological form, and it has long been the aim of topology to treat this form all at once.
L. H. Kauffman, Knots and Physics, 1992.
I believe there is a similarity between the concept of learning and the concept of land as something to be inherited from those who come before us: something that can be handed down from generation to generation as a precious and irreplaceable object; I think we have lost sight of a very important philosophy that education is an invaluable gift.
Koji Shiga, A Mathematical Gift, 1995.
1. Omeomorfismi e isotopie di nodi, manici e buchi
Il concetto di omeomorfismo è alla base dell’intera topologia e in particolare della topologia algebrica e differenziale. Esso permette di definire in termini profondi quando due superfici, spazi o varietà sono topologicamente equivalenti, cioè trasformabili l’una nell’altra tramite una famiglia di deformazioni continue senza strappi e rotture. Si può così mostrare, ad esempio, che (a) la sfera con un manico è omeomorfa al toro con un buco ; (b) il toro con due buchi è omeomorfa alla sfera con due manici ; (c) il toro con un buco e un disco è omeomorfa alla sfera con un manico e un disco.
L’idea intuitiva di deformazione/trasformazione continua, sui cui si fonda la topologia, è ben radicata nelle nostre strutture mentali, più del concetto di isometria o similitudine, perché legata alla percezione della nostra identità e integrità corporea in continua evoluzione. Purtroppo però non è possibile trattare le trasformazioni continue dal punto di vista matematico in modo altrettanto elementare (non bastano le trasformazioni lineari).
Nello spirito di Klein e Poincaré, fare della topologia in Rn significa studiare questo spazio e i suoi sottospazi a meno del gruppo delle trasformazioni topologiche (o omeomorfismi), cioè delle applicazioni biunivoche g : Rn → Rn tali che g e g–1 sono continue. In particolare, consideriamo i seguenti sottospazi del piano/spazio euclideo : la circonferenza S1 = {x ∈ R2 | ||x|| = 1} ⊂ R2, la sfera S2 = {x ∈ R3 | ||x|| = 1} ⊂ R3 e il toro T = S1 ⊂ R2 x R2 ≅ R4. La sfera e il toro sono superfici (connesse e compatte) e possono essere entrambe pensate come ampliamenti (compattificazioni) del piano euclideo con l’aggiunta di “punti all’infinito”. Per questo è spesso interessante adottare la sfera e il toro come ambienti di lavoro alternativi al piano. La sfera si può ottenere dal piano euclideo con l’aggiunta di un solo punto all’infinito, cioè S2 ≅ = R2 ∪{∞} (compattificazione di Alexandroff). Ponendo ∞ = (0,0,1) ∈ S2 (polo nord della sfera), la proiezione stereografica φ : S2 – {∞} → R2 da su R2 ⊂ R3 dà un’equivalenza topologica S2 – {∞} ≅ R2. Poiché tutti i punti della sfera sono equivalenti a meno di rotazioni, un’analoga equivalenza topologica S2 – {p} ≅ R2 si ha per ogni punto p ∈ S2.
Il toro è costruito nello spazio euclideo quadridimensionale, ma può in effetti essere anche realizzato come superficie di rotazione nello spazio tridimensionale, e quindi pensato come sottospazio di R3. Questa rappresentazione consente anche di visualizzare T come ampliamento di R2 : possiamo pensare come insieme di punti all’infinito l’unione del meridiano e del parallelo tracciati nella figura di un toro di rotazione in R3. La superficie ottenuta ruotando il meridiano M ⊂ R3 (di equazioni x2 + z2 + 4x + 3 = 0 e y = 0) intorno all’asse z è topologicamente equivalente al toro T. Inoltre, se P è il parallelo (di equazioni x2 + y2 = 4 e z = 1), allora T\(M ∪ P) è topologicamente equivalente a un quadrato (aperto) nel piano euclideo, quindi si ha T \(M ∪ P) ≅ R2.
1.1. Trasformazioni topologiche e deformazioni continue : isotopie ambientali
Abbiamo già accennato al nesso profondo che esiste tra le trasformazioni topologiche dello spazio e l’idea intuitiva di “deformazione continua”. Tale nesso può essere chiarito in termini formali tramite la nozione di isotopia.
Definizione 1. Due applicazioni continue, ƒ, g : X → Y tra spazi topologici sono omotope se esiste una famiglia di applicazioni ht : X → Y che dipendono in modo continuo dal parametro t ∈ [0, 1], tale che h0 = ƒ e h1 = g. Più precisamente si richiede che sia continua l’applicazione H : X x [0, 1] → Y definita da H (x, t) = ht(x) per ogni (x, t) ∈ X x [0, 1]. H è detta omotopia tra ƒ e g.
Definizione 2. Due trasformazioni topologiche (cioè omeomorfismi) ƒ, g : S → S di uno spazio topologico S sono isotope se esiste un’omotopia H fra ƒ e g come nella definizione precedente, tale che h : S → S è una trasformazione topologica per ogni t ∈ [0, 1]. In tal caso H è detta isotopia fra ƒ e g. Inoltre, se ƒ è l’identità di S, allora diciamo che g : S → S è realizzabile mediante isotopia.
Se in quest’ultima definizione si interpreta t come parametro temporale, si può dire che le trasformazioni topologiche realizzabili mediante isotopia sono quelle che si possono ottenere con deformazioni continue dello spazio S.
1.2. Equivalenze topologiche
Il concetto di omeomorfismo è essenziale per capire il problema delle equivalenze topologiche tra spazi. Formalmente, diremmo che due spazi topologici X e Y sono topologicamente equivalenti (omeomorfi) se esiste un omeomorfismo h : X → Y, cioè un’applicazione biunivoca tale che h e h–1 sono entrambe continue. In tal caso scriviamo X ≅ Y e gli spazi X e Y hanno le stesse proprietà topologiche. Per esempio X e Y hanno lo stesso numero di componenti connesse (cioè, in termini intuitivi, sono costituiti dallo stesso numero di “pezzi”).
Definizione 3. Sia S uno spazio topologico e siano X, Y ⊂ S due sottoinsiemi (“oggetti” in S). Allora diciamo che X e Y sono topologicamente equivalenti in S e scriviamo X ≅S Y, se esiste una trasformazione topologica g : S → S tale che g(X) = Y. Inoltre, diciamo che X e Y sono isotopicamente equivalenti in S (o isotopi in S) e scriviamo X ≡S Y, se g è realizzabile mediante isotopia.
Ad esempio, il quadrato Q = [–1, 1]2 ⊂ R2 e il disco unitario D = {x ∈ R2 | ||x|| ≤ 1} ⊂ R2 sono isotopicamente equivalenti in R2 ; abbiamo così, mediante una serie di deformazioni continue, un’equivalenza isotopica Q ≡R2 D. È facile verificare che ≅S e ≡S sono relazioni di equivalenza tra sottoinsiemi di S (ciò equivale a dire che le trasformazioni che le definiscono formano dei gruppi). Inoltre, vale ovviamente l’implicazione X ≡S Y ⇒ X ≅S Y per ogni X, Y ⊂ S, mentre non vale l’implicazione inversa.
D’altra parte, se X e Y si pensano come spazi topologici con la topologia indotta da S, allora vale anche l’implicazione X ≅S Y ⇒ X ≅ Y, mentre non vale l’implicazione inversa. In particolare, se X e Y sono topologicamente equivalenti in S, allora devono avere lo stesso numero di componenti connesse, così come i loro complementari S \ X e S \Y (infatti si ha anche S \ X ≅S S \Y).
1.3. Superfici, bordi e anse
- Note de bas de page 1 :
-
Cfr. R. Thom, Esquisse d’une Sémiophysique, InterEditions, Parigi, 1988.
- Note de bas de page 2 :
-
Si veda L. Boi, Morphologie de l’Invisible, Presses Universitaires de Limoges, Limoges, 2011.
Entriamo adesso nel mondo infinito e ancora in gran parte misterioso delle superfici, e cerchiamo di rivolgere il nostro guardo al loro interno, cioè al mondo, anzi ai mondi che esse possono racchiudere ; lo sguardo non deve essere di quelli (fondati sul mero senso della vista) che cercano una conferma ai nostri schemi e pensieri, ma bensì un’esplorazione che ci mette sulle tracce del nuovo e dell’inatteso, e che, in quanto tale, può suscitare la nostra più profonda meraviglia. Naturalmente, per poter penetrare una superficie e coglierne le sue trasformazioni interne dobbiamo “vederla” non come semplice oggetto inerte e amorfo, ma piuttosto come un mondo stratificato spazialmente e sedimentato nel (e dal) tempo, che può inoltre cambiare di aspetto e di forma sotto l’effetto di fenomeni, eventi, situazioni accidentali e condizioni necessarie in quello che (seguendo René Thom1) si potrebbe chiamare un flusso continuo e discontinuo di azioni e retroazioni fra pregnanze e salienze. Sono le diverse combinazioni e configurazioni di questo flusso che nel corso dell’esperienza, dell’osservazione e dell’introspezione incontrano il mondo della nostra percezione e cognizione. Si costituisce così, a partire da questo nuovo materiale composito che rappresenta un nuovo livello di realtà, il mondo delle tessiture (altrettanti motivi ed eventi emergenti nelle cose), delle qualità sensibili e delle forme estetiche. Qui non parleremmo di questi aspetti importanti2, ma solo di alcune proprietà matematiche salienti delle superfici.
Una superficie topologica è uno spazio topologico X localmente equivalente al piano euclideo, cioè intorno ad ogni suo punto X ammette un sistema di coordinate costituito da due parametri reali. X è orientabile se è possibile scegliere questi sistemi di coordinate locali orientati coerentemente ; ciò equivale a dire che X non contiene nessun ciclo che inverte l’orientazione, o in altre parole X non contiene nessun nastro di Möbius.
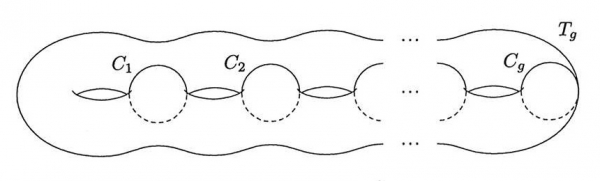
Il genere g(X) di una superficie orientabile connessa X è definito come il massimo numero m per cui esistono C1, … , Cm ⊂ X curve chiuse semplici (cioè omeomorfe a S1) tali che X \ (C1 ∪ … ∪ Cm) è ancora connesso. Si dimostra che tale massimo esiste (finito) se X è compatta. Ragionando per induzione su g ≥ 0, si dimostra che la superficie Tg rappresentata in figura 1 è una superficie orientabile di genere g. Per g = 0 ciò segue dal teorema di Jordan in quanto T0 = S2 ; per g = 1 si ha T1 = T.
Figura 1. Superficie orientabile di genere g.
D’altra parte, il genere è un invariante topologico (superfici omeomorfe hanno lo stesso genere) che consente di classificare completamente le superfici orientabili connesse e compatte. Infatti vale il seguente teorema.
Teorema 1. Due superfici topologiche orientabili connesse e compatte sono omeomorfe se e solo se hanno lo stesso genere. In particolare, per ogni superficie topologica orientabile connessa e compatta X si ha X ≅ Tg con g = g(X).
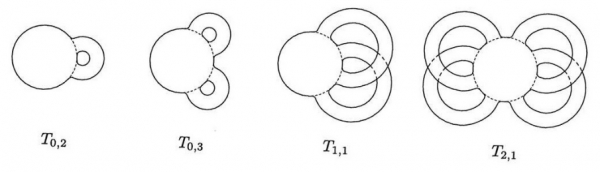
Nel seguito considereremmo superfici topologiche con bordo, cioè porzioni chiuse di superfici delimitate da curve topologiche che ne costituiscono il bordo. Per una superficie topologica orientabile connessa X con bordo definiamo il genere g(X) come sopra, vincolando le curve Ci a non incontrare il bordo, e denotiamo con b(X) il numero delle componenti connesse del bordo (b(X) = 0 nel caso in cui X sia senza bordo, cioè il caso trattato sopra). Se X è compatta g(X) e b(X) sono entrambi finiti e tutte le componenti connesse del bordo sono omeomorfe a S1. Per ogni g, b ≥ 0, la superficie Tg,b che si ottiene togliendo b dischi aperti da Tg è una superficie orientabile connessa compatta di genere g con b componenti di bordo. Il teorema 1 si può estendere alle superfici con bordi come segue.
Teorema 2. Due superfici topologiche orientabili connesse e compatte con bordo sono omeomorfe se e solo se hanno lo stesso genere e lo stesso numero di componenti di bordo. In particolare, per ogni superficie topologica orientabile connessa e compatta X con bordo si ha X ≅ Tg,b con g = g(X) e b = b(X).
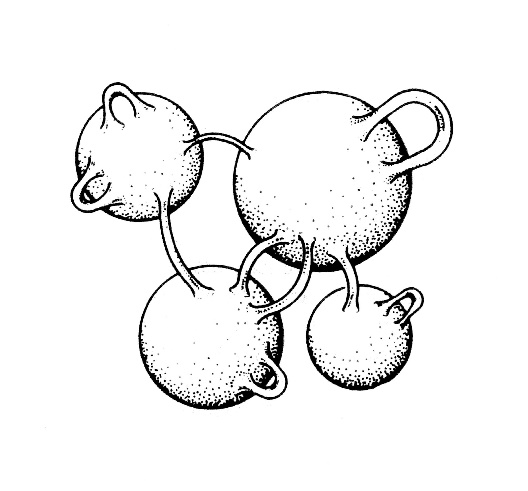
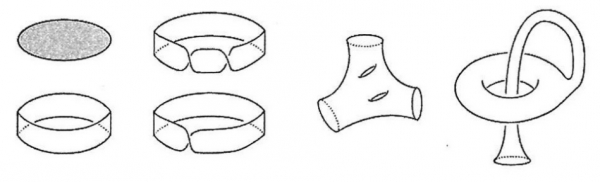
Ogni superficie topologica orientabile connessa e compatta X con bordo non vuoto, si può ottenere incollando 2g(X) + b(X) – 1 bande (o anse) al bordo di un disco (fig. 2).
Figura 2. Superfici orientabili con bordo ottenute incollando bande (anse) a un disco.
Figura 2.1. Le anse diventano dei cunicoli che possono collegare diversi universi tra di loro.
Ogni superficie topologica compatta X con bordo (eventualmente vuoto) ammette una poligonazione, cioè una decomposizione X = P1 ∪ … ∪ Pn come unione di poligoni topologici (copie omeomorfe di poligoni euclidei), con la proprietà che due poligoni possono incontrarsi solo in vertici e/o lati comuni. Per esempio, le superfici che delimitano i poligoni platonici inscritti in S2 ⊂ R3 sono topologicamente equivalenti a S2 (mediante proiezione dal centro) e inducono poligonazioni di S2.
Teorema 3. Sia X una superficie topologica compatta con bordo (eventualmente vuoto). Se P è une poligonazione di X, denotiamo con v(P), s(P) e p(P) rispettivamente il numero di vertici, degli spigoli e dei poligoni di P. Il numero intero χ (X) = v(P) – s(P) + p(P) è un invariante topologico di X, la caratteristica di Eulero di X, che non dipende dalla particolare poligonazione P.
La dimostrazione di questo teorema si basa sul fatto che, a meno di omeomorfismi, due poligonazioni di X possiedono una suddivisione comune in poligoni più piccoli. Allora, l’indipendenza di χ (X) da P si riduce sostanzialmente al caso delle triangolazioni lineari di poligoni euclidei. Se X è un poligono euclideo e P è una sua triangolazione lineare (cioè, poligonazione in triangoli euclidei), allora si ha v(P) – s(P) + p(P) = 1. Alla luce del teorema 3 è facile verificare la relazione tra χ(X), g(X) e b(X) data da quanto segue. Questo mostra che due qualunque di tali invarianti topologici bastano a classificare le superfici orientabili connesse e compatte con bordo. Infatti, per ogni X superficie topologica orientabile, connessa e compatta, con bordo (eventualmente vuoto), si ha : χ (X) = 2 – 2g(X) – b(X).
2. Somme connesse di spazi 3-dimensionali e di nodi
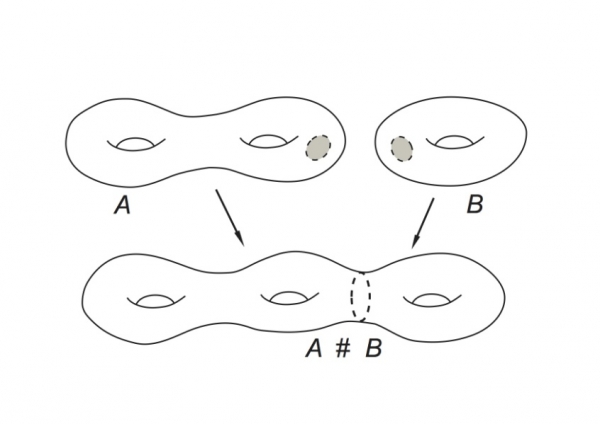
Un altro concetto fondamentale della topologia è quello di somma connessa di due varietà (siano esse superfici o spazi a tre o più dimensioni). Questo concetto ha un ruolo particolarmente importante nella teoria topologica dei nodi. Infatti, molti nodi si possono ottenere come somma connessa di due nodi più semplici. Per esempio, il nodo composto in figura 3 si ottiene come somma connessa del nodo a trifoglio (a sinistra) e il nodo a otto (a destra). Questo nodo non è primo. (Un nodo è primo se non è ottenibile come somma connessa di due nodi distinti). Esiste una semplice operazione che permette di “unire” due nodi per costruirne un terzo : questa operazione di chiama somma connessa.
Figura 3. Somma connessa di nodi.
Figura 3.1. Somma connessa di superfici.
Esiste un importante teorema, enunciato e dimostrato dal matematico tedesco Horst Schubert nel 1949, il quale asserisce che ogni nodo si ottiene in modo unico come somma connessa di una successione di nodi elementari denominati, similarmente alla nomenclatura dei numeri, nodi primi. Il teorema è in effetti l’analogo del teorema fondamentale dell’aritmetica nel contesto dei nodi, dove l’operazione di moltiplicazione è sostituita con la somma connessa fra nodi. La somma connessa fra nodi è un’operazione che presenta alcune analogie con la somma connessa fra varietà. Come per le varietà, questa operazione non dipende dal tipo di diagramma scelto per rappresentare i nodi, né dal “nastro” scelto su cui operare la somma connessa. La somma connessa di due nodi K e H si indica con K # H. L’operazione di somma connessa è commutativa e associativa. Il nodo banale O è l’elemento neutro dell’operazione, ovvero O # K = K # O = K per ogni altro nodo K. Come per le 2- e 3-varietà, esiste un Teorema di fattorizzazione in nodi primi (vedasi sopra per l’enunciato).
Ricordiamo brevemente la definizione di somma connessa per varietà differenziabili. Cominciamo dalle superfici (varietà a due dimensioni). Per ottenere la somma connessa di due superfici si rimuovono le parti interne di due dischi, e si incollano le due circonferenze rimanenti. Il risultato di questa operazione è una nuova figura (si veda la figura 3.1). Passiamo ora alla definizione formale più generale. Siano M e N due varietà topologiche della stessa dimensione n. Siano BM e BN due aperti rispettivamente in M e N, le cui chiusure sono entrambe omeomorfe al disco chiuso n-dimensionale Dn = {x ∈ Rn | |x| ≤ 1}. Quindi BM e BN sono entrambe omeomorfe alla palla aperta Bn = {x ∈ Rn | |x| < 1} ed il bordo è omeomorfo alla sfera (n–1)-dimensionale Sn-1 = {x ∈ Rn | |x| = 1}. Sia quindi ψ un fissato omeomorfismo ψ : ∂BN → ∂BM. La somma connessa di M e N è quindi definita come lo spazio che si ottiene rimuovendo le due palle aperte da M e N ed incollando successivamente i nuovi bordi sferici tramite la mappa (funzione) ψ. Questo spazio viene indicato con M # N ed è anch’esso una varietà n-dimensionale. Formalmente : M # N = (M \ BM) ∪ (N \ BN)/ ∼dove ∼ è la relazione di equivalenza che identifica ogni x in ∂BM con l’immagine ψ (x) in BN. La varietà ottenuta M # N dipende dalla scelta degli aperti BM, BN e dall’omeomorfismo ψ. Se però le varietà M, N sono differenziabili, e ogni omeomorfismo nella definizione è in verità un diffeomorfismo, la scelta degli aperti non influisce sul risultato. D’altro canto, se l’omeomorfismo ψ è sostituito con un altro omeomorfismo ψ’ omotopo a ψ il risultato non cambia. A meno di omotopia, vi sono solo due omeomorfismi di Sn–1 in sé : quello che mantiene l’orientazione della sfera e quello che la inverte. Quindi ci sono due possibili risultati. Di conseguenza, se le varietà sono differenziabili la somma connessa M # N dipende soltanto dall’orientazione della mappa d’incollamento ψ. In dimensioni 2 e 3, una varietà differenziabile M è prima se non è ottenibile come somma connessa M = N ∈ N’, dove entrambi i fattori N e N’ sono diversi dalla sfera a n dimensioni Sn.
La classificazione delle superfici e il teorema di Kneser-Milnor sostengono rispettivamente che ogni 2- o 3-varietà M orientabile compatta è ottenibile in modo unico come prodotto di varietà prime : M = N1 # N2 # …. # Mk. In dimensione 2, le varietà prime orientabili e compatte sono la sfera ed il toro. In dimensione 3, le 3-varietà prime sono infinite e non sono ancora state classificate in modo soddisfacente. Non esiste un teorema analogo per le varietà di dimensione 4 o superiore.
In altri termini, il teorema di Kneser-Milnor asserisce che ogni 3-varietà compatta orientabile M diversa dalla sfera S3 può essere ottenuta come somma connessa di 3-varietà prime N1, …, Nk diverse da S3 : M = N1 # … # Nk. Le k varietà prime Ni sono inoltre univocamente determinate da M. L’enunciato ha la stessa forma del teorema fondamentale dell’aritmetica. La sfera S3 gioca il ruolo del numero 1 per gli interi, cioè dell’elemento neutro rispetto all’operazione di somma connessa.
2.1. Spazi irriducibili e spazi riducibili
Le 3-varietà non ottenibili mediante il procedimento menzionato sopra sono dette irriducibili ; in altri termini, si può mostrare che una varietà irriducibile M è effettivamente prima. Esse sono studiate dalla topologia della dimensione bassa. Una 3-varietà irriducibile è una 3-varietà in cui ogni sfera borda una palla. Più rigorosamente, una 3-varietà differenziabile connessa M è irriducibile se ogni sottovarietà differenziabile S omeomorfa ad una sfera è bordo S = ∂D di un sottoinsieme D omeomorfo alla palla chiusa : D3 = {x ∈ R3 ||x| ≤ 1}. L’ipotesi di differenziabilità per M non è importante, perché ogni 3-varietà topologica ha un’unica struttura differenziabile. L’ipotesi che la sfera sia liscia (cioè che sia una sottovarietà differenziabile) è invece importante : la sfera deve avere infatti un intorno tubolare. Una 3-varietà che contiene una sfera non bordante una palla è invece detta riducibile : questa può essere effettivamente “ridotta” ad una varietà più semplice tramite l’operazione inversa della somma connessa. Una 3-varietà è prima se non è ottenuta come somma connessa non banale di due varietà. I concetti di irriducibile e prima sono equivalenti per tutte le 3-varietà, con due sole eccezioni : il prodotto S2 x S1 ed il fibrato non orientabile di sfere su S1 sono entrambe prime ma non irriducibili. Una 3-varietà connessa M è prima se non è ottenibile come somma connessa M = N1 # N2 di due varietà entrambe distinte da S3 (o, analogamente, entrambe distinte da M).
Diamo alcuni esempi di spazi irriducibili e di spazi riducibili. Lo spazio euclideo tridimensionale R3 è irriducibile : ogni sfera liscia nello spazio borda effettivamente una palla. D’altra parte, la sfera di Alexander (detta anche sfera cornuta) è una sfera in R3 non liscia, che non borda una palla : l’ipotesi sulla “liscezza” della sfera è quindi necessaria. La sfera S3 è irriducibile. Lo spazio prodotto S2 x S1 non è irriducibile : infatti la sfera S2 x {pt} (dove “pt” è un qualsiasi punto di S1) ha complementare connesso, e quindi non può essere bordo di una palla. Uno spazio lenticolare L(p, q) con p ≠ 0 (distinto quindi da S2 x S1) è irriducibile.
2.2. La sfera cornuta : un esempio di oggetto topologico con proprietà patologiche
Ricordiamo che la sfera di Alexander è un oggetto topologico, ossia una superficie nello spazio omeomorfa ad una sfera, ma con proprietà molto diverse (esotiche) dalla sfera usuale (da qui il nome di “mostro” matematico). La sfera di Alexander è costruita come bordo di un oggetto tridimensionale, definito iterando infinite volte la costruzione mostrata nella figura 3.2. La costruzione parte da un “arco solido” di toro solido, avente due estremità. Il procedimento iterativo consiste nell’aggiungere ad ogni estremità un altro arco solido analogo, più piccolo (le “corna”) : così, il numero di estremità raddoppia. Il risultato di questo procedimento è un oggetto omeomorfo ad un albero con rami che si diramano infinitamente. Se i rami non si diramassero infinitamente, ma fossero finiti, questo oggetto sarebbe omeomorfo al disco tridimensionale : D = {x ∈ R3 ||x| ≤ 1}. Poiché i rami sono infiniti in tutte le direzioni, l’oggetto descritto è invece omeomorfo al disco a cui è stato rimosso un insieme di Cantor contenuto nel bordo. Ogni punto di questo insieme di Cantor corrisponde ad un percorso infinito lungo i rami, definito da una sequenza infinita di lettere “s” e “d”, corrispondenti alla svolta (a “sinistra” o “destra”) effettuata ad ogni diramazione. La chiusura di questo oggetto in R3 è omeomorfa al disco : ogni percorso infatti ha come limite un punto dello spazio, e percorsi diversi hanno limiti diversi. Il bordo della chiusura è quindi omeomorfo ad una sfera : questa è la sfera di Alexander. Pur essendo omeomorfa alla sfera standard : S2 = {x ∈ R3 | |x| = 1}, essa è contenuta nello spazio in modo molto differente. Come la sfera standard, separa lo spazio in due zone : quella interna e quella esterna ; quella interna è una palla. Quella esterna è però notevolmente differente : non è semplicemente connessa (mentre la parte esterna della sfera lo è) ; infatti una curva semplice chiusa che allaccia un qualsiasi ramo non è contraibile tramite una omotopia. Ne consegue che non esiste nessun omeomorfismo dello spazio che porti S2 nella sfera di Alexander. La sfera di Alexander non è una superficie differenziabile dello spazio R3 : non è infatti differenziabile nei punti dell’insieme di Cantor aggiunto al limite. In questi punti non è ad esempio definito un piano tangente.
Figura 3.2. La sfera di Alexander. Si tratta di un oggetto topologico che presenta certe proprietà topologiche non comuni.
2.2. Nodi come contorni di superfici
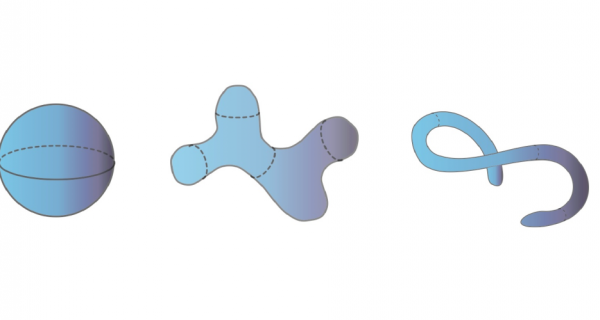
Ci sono delle superfici che sono isotope tra di loro. Una isotopia la si definisce come una deformazione continua dello spazio-ambiente che porta a far coincidere due superfici che vi sono immerse. Per esempio, è possibile realizzare una isotopia tra queste tre superfici (fig. 4).
Figura 4. Queste superfici sono isotope.
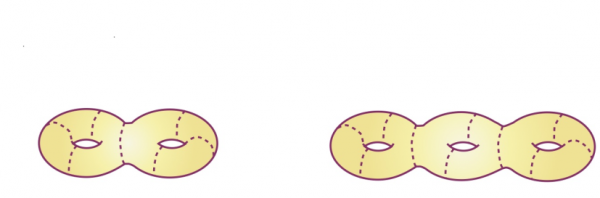
Figura 4.1. Queste superfici sono isotope e hanno lo stesso genere (lo stesso numero di buchi).
Figura 4.2. Queste superfici non sono isotope e differiscono nel loro genere.
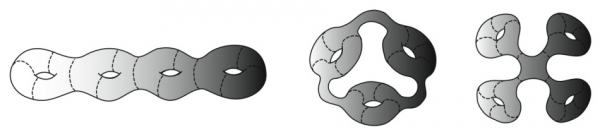
La superficie Sg di genere g si può ottenere deformando la superficie S qui sotto in modo continuo. Tuttavia la deformazione continua mostrata nella figura 5 ha un significato più ampio ; infatti, essa consente alla superficie di torcersi e attorcigliarsi intorno ai buchi della superficie S, in modo tale che la nuova superficie risulti alla fine annodata. Si può inoltre mostrare come sia possibile costruire una superficie perforata di un determinato numero di buchi, in modo tale che ci si possa iscrivere un nodo senza che i suoi cappi si rompano (fig. 5).
Figura 5. Qui sono mostrate due deformazioni continue. Naturalmente ne esiste una terza tra le due superfici a destra nell’immagine (da sopra verso sotto). Si tratta, in tutti e tre i casi, di omeomorfismi.
Figura 6. Superficie multiannodata di genere g. La superficie passa attraverso i suoi buchi generando un intreccio complesso.
Quanti buchi ci sono in questa superficie ? E come possiamo contarli ? La caratteristica di Eulero permette di dare una risposta. Si tratta di identificare e contare il numero di face, lati e vertici dei triangoli “incollati” a questa scultura. In questo modo otteniamo la caratteristica di Eulero della superficie usando il metodo di triangolazione. La caratteristica di Eulero di questa superficie è – 2. Infatti, dal punto di vista topologico essa è equivalente alla sfera S2, ma non lo è dal punto di vista differenziabile : in effetti, è impossibile ottenere questa superficie da una palla con due buchi per deformazione continua, a meno di ammettere auto-intersezioni. Tuttavia, si può ottenere questa superficie senza auto-intersezioni se la deformazione della palla avviene in uno spazio a quattro dimensioni invece che nello spazio tridimensionale usuale.
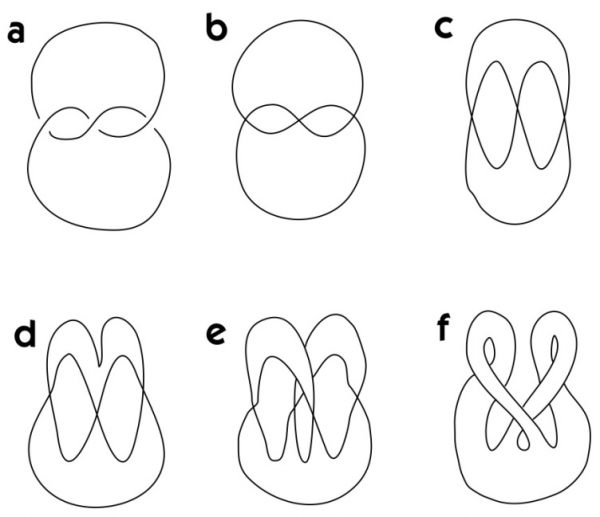
Molti nodi, è il caso del nodo a trifoglio e del nodo a otto, formano il contorno di una superficie. Questi contorni separano ciascuna delle superfici corrispondenti in due parti. Questi due nodi hanno lo stesso genere, che è uguale a 1. Lo si può infatti disegnare sulla superficie di una sfera con due manici : si ottengono due parti separate della superficie quando la si taglia lungo la curva del nodo.
Figura 7. Il nodo a trifoglio (a) e il nodo a otto (b) formano il contorno di una superficie.
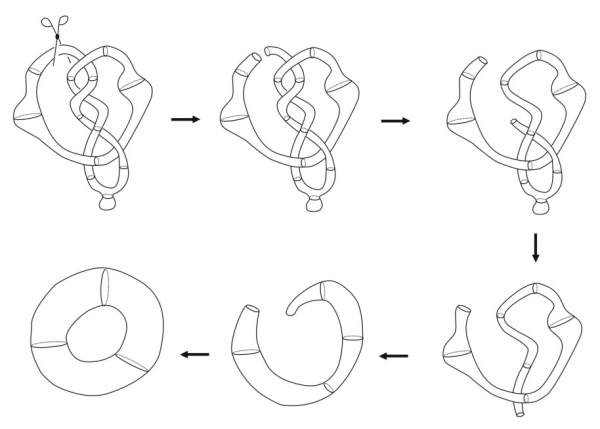
È possibile “iscrivere” un nodo su una superficie in modo tale che il nodo appaia sul contorno di questa superficie che la separa dunque in due parti quando la si taglia seguendo il suo contorno. Il numero di manici di questa superficie determina il genere del nodo. Per costruire tale superficie (fig. 8), per esempio quella che corrisponde al nodo a trifoglio, si parte dal disegno del nodo (a) e si riempie “l’interno” del nodo con una superficie di cui i contorni sono costituiti dal disegno del nodo (b). Possiamo immaginare che questa superficie è quella realizzata da una bolla di sapone che si appoggia sulla curva chiusa che forma il nodo ; si deforma questa superficie rendendo ovali i buchi per ottenere la superficie (c). Si passa poi a intagliare la superficie, così come è rappresentata sulla parte superiore della superficie (d). Quando questa scanalatura attraversa il tortiglione (la treccia) centrale, si ottiene la figura (e). Ci si può convincere, per mezzo di una linguetta di carta, che questi due tortiglioni (trecce) si combinano per dare luogo a un laccio (ansa, looping) e, di conseguenza, si ottiene la superficie (f). Infondendo dell’aria tra i due lati di questa superficie, si trova un volume il cui contorno è il nodo a trifoglio, e il cui genere è uguale a 1, poiché la sfera generalizzata che si ottiene ha due manici (quindi quattro buchi).
Figura 8. “Iscrizione” di un nodo su una superficie.
Ricordiamo infine che il genere di un nodo composto prodotto di due nodi è superiore o uguale al genere di ogni singolo nodo. La prova sperimentale consiste nel distendere il nodo in maniera tale che un piano tagli soltanto due fili o cappi del nodo composto A # B ; in tal modo i nodi A e B risultano separati. Appare chiaramente che la somma del numero di manici di A e B è uguale al numero di manici della sfera iniziale e, di conseguenza, che il genere del nodo composto è superiore o uguale alla somma dei generi rispettivi di A e B.
Figura 9.
3. Alcuni concetti “elementari” della teoria topologica dei nodi
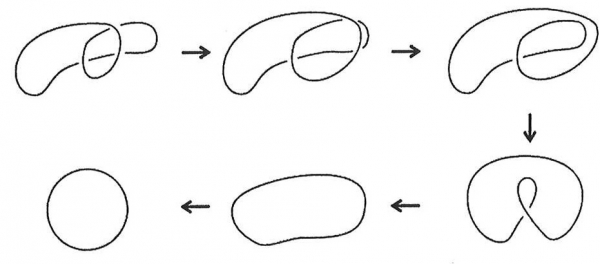
I nodi, cioè i pezzi di spago variamente ingarbugliati, sono tra gli oggetti di interesse primario della topologia. La nozione di equivalenza è fondamentale per capire e decidere che due nodi sono uguali (oppure non lo sono). Esiste una differenza sostanziale tra l’osservazione di un nodo dall’esterno e quella dall’interno. Su un nodo è sempre possibile “appoggiare” (in molti modi) una superficie ; in altre parole, a partire da un nodo si può creare uno spazio, e nodi diversi possono dar luogo a spazi diversi. Secondo il punto di vista di un topologo, si può considerare che due oggetti sono uguali quando li si può deformare, senza strappi, l’uno nell’altro. Per un topologo, un nodo è un oggetto nello spazio ottenuto da una corda sottilissima (idealmente senza spessore), perfettamente flessibile ed elastica, con la quale viene formato un garbuglio e della quale alla fine vengono saldati insieme i due estremi. Dunque, due nodi sono tra loro equivalenti quando si possono deformare l’uno nell’altro senza strappi o rotture. Tuttavia, per stabilire che due nodi non sono equivalenti non basta un numero anche molto grande di tentativi falliti di deformarli l’uno nell’altro : serve un argomento generale capace di mostrare che nessuna deformazione potrà mai trasformare un nodo nell’altro.
Figura 10. Una deformazione del nodo banale.
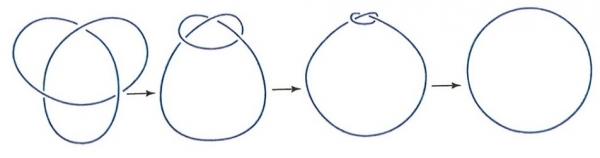
Figura 11. Deformazione planare di un diagramma di nodo. Un nodo trifoglio può essere deformato in un nodo banale (cioè una circonferenza), senza strappi e rotture.
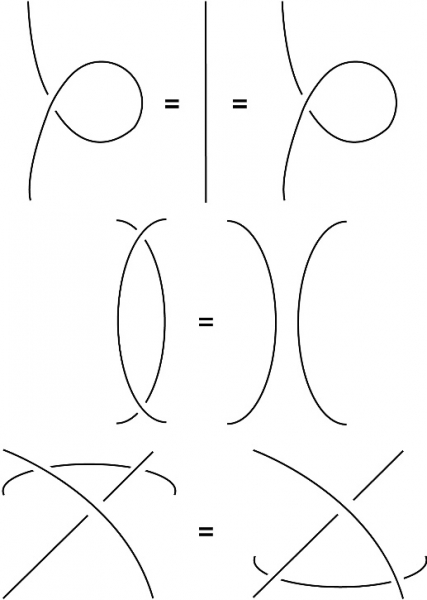
Figura 12. Le mosse I, II e III di Reidemeister. Si tratta di movimenti applicati a diagrammi planari di nodi che consentono di effettuare o sciogliere un nodo nello spazio.
Una nozione molto importante è quella di diagramma di un nodo. In matematica si chiama proiezione ortogonale di un oggetto su un piano la figura piatta che si ottiene riportando sul piano tutti i punti dell’oggetto lungo la direzione perpendicolare al piano (questa definizione è analoga a quella usata nella geometria proiettiva e nella prospettiva per proiettare le caratteristiche di un oggetto tridimensionale o di un volume sulla sua immagine planare, bidimensionale ; si veda sotto). Si chiama diagramma di un nodo una sua proiezione ortogonale con interruzione ad ogni incrocio del ramo più lontano dal piano di proiezione. (Bisogna stare attenti al fatto che possono presentarsi delle proiezioni “non valide” di un nodo : un punto in cui la curva è liscia (cuspide) ; un punto in cui due rami della curva si toccano.) L’uso di tali diagrammi traduce l’idea di deformazione. Esiste infatti una sequenza di (tre) mosse che permette di cambiare l’immagine di un nodo in un’immagine differente dello stesso nodo. Questo processo si chiama deformazione planare di un diagramma di nodo, nel corso del quale cambia il diagramma o la presentazione del nodo nel piano, sebbene la sua struttura topologica interna si conservi. Le trasformazioni menzionate si chiamano mosse di Reidemeister e vanno intese nel modo seguente : dato un diagramma di nodo, si seleziona una porzione del diagramma che appaia come uno qualsiasi dei frammenti nella figura 12, quindi, lasciando inalterato il resto del diagramma, si sostituisce la porzione prescelta con il frammento nella figura 14 collegato con una doppia freccia a quello precedente. Si ha così il seguente teorema.
Teorema. Ogni diagramma rappresenta un nodo. Ogni nodo può essere rappresentato da diagrammi. Due diagrammi rappresentano nodi equivalenti precisamente quando si possono ottenere l’uno dall’altro tramite deformazione piana ed esecuzione (ripetuta) di mosse di Reidemeister.
Fig. 13. Due link distinti con complementari uguali.
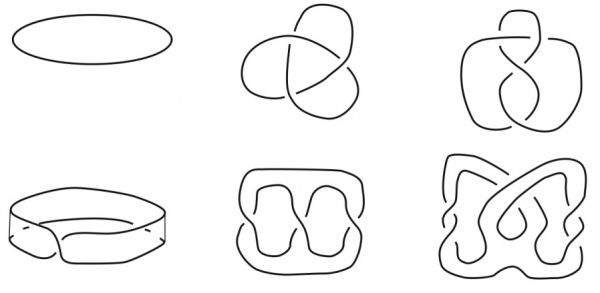
Fig. 14. Alcune superfici senza bordo.
Figura 14.1. Alcune superfici con bordo.
Fig. 15. Superfici senza bordo intrinsecamente uguali.
Fig. 16. Due superfici knot-spanning per il nodo banale, due per il nodo a trifoglio e due per il nodo a otto.
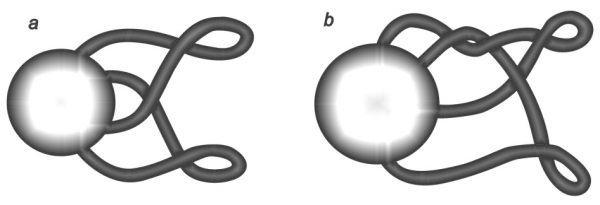
Introduciamo ora il concetto importante di complementare del nodo. Esso si ottiene quando si considera, piuttosto che il nodo, ciò che resta dello spazio tridimensionale una volta che il nodo é stato rimosso. Una definizione più formale si può enunciare come segue : il complementare di un nodo è lo spazio tridimensionale escluso il nodo medesimo, cioè il campo di osservazione ed esperienza di qualcuno cui si dia licenza di spostarsi come gli pare purché non tocchi (né arrivi mai a vedere) il nodo.
Si può parlare di un punto di vista intrinseco e di uno estrinseco nell’osservare un nodo. Il concetto del complementare di un nodo suggerisce l’idea che un oggetto di interesse topologico si possa guardare “dal di dentro”. In quel caso, l’oggetto da esaminare dall’interno è proprio l’esterno del nodo, cioè quello che resta del nostro mondo spaziale tridimensionale una volta immaginato di aver rimosso il nodo. Ma la stessa operazione di restrizione di visuale la si può fare (e anzi è molto più semplice) per il nodo stesso piuttosto che per il suo complementare. L’idea consiste a immedesimarsi in un abitante del nodo, cioè in qualcuno per il quale il nodo rappresenta l’unico orizzonte, senza alcuna possibilità di contemplarne l’esterno. Se ci si piazza sul nodo stesso e si effettuano un certo tipo di operazioni (ad esempio, tagliando un nodo a trifoglio in un punto, deformando e poi riattaccando, si ottiene il nodo banale), allora, dal punto di vista intrinseco, ogni nodo è equivalente al nodo banale. Invece, dal punto di vista estrinseco, cioè delle deformazioni spaziali, il nodo a trifoglio non è equivalente a quello banale. In realtà si può dire molto di più : esistono infiniti nodi estrinsecamente distinti, ovvero due a due non equivalenti tra loro tramite deformazioni.
- Note de bas de page 3 :
-
Questo risultato fondamentale della teoria topologica dei nodi si trova enunciato e dimostrato in C. M. Gordon e J. Luecke, “Knots are determined by their complements”, J. Amer. Math. Soc., 2 (1989), 371-415.
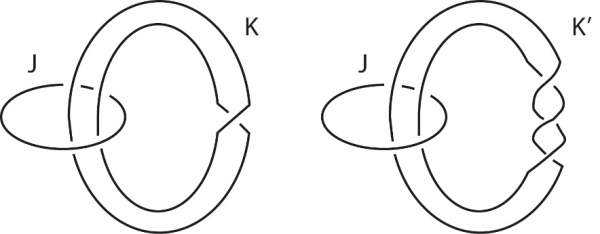
Per chiarire maggiormente questo punto, esaminiamo un fenomeno che potrà sembrare sorprendente. Consideriamo due link (un link è un oggetto formato da due o più nodi che non si toccano a vicenda ma che possono intrecciarsi fra loro), entrambi aventi due componenti nodo, dunque intrinsecamente uguali. Invece non è difficile vedere che estrinsecamente sono diversi : nel link a sinistra (nella figura 13) ciascuna delle due componenti presa come nodo è un nodo banale, mentre nel link a destra (nella stessa figura) le due componenti sono un nodo banale e un nodo a trifoglio. È possibile verificare che i complementari dei due link sono intrinsecamente uguali. Questo esempio mostra che link non equivalenti possono avere complementari uguali. Con questo in mente si potrà apprezzare il seguente risultato di eccezionale difficoltà, che ha richiesto ai matematici decenni di sforzi : se due nodi hanno complementari intrinsecamente uguali allora sono equivalenti per deformazione3.
Ritorniamo alla visione “estrinseca” e “intrinseca” di un nodo. Dicendo che un nodo è una corda ingarbugliata di spessore nullo indubbiamente sto pensando di vedere il nodo dall’esterno (anche se altre rappresentazioni possono venirmi in mente, come quella, ad esempio, di un insieme di orbite caotiche o quella di un campo elettromagnetico con indice di torsione estremamente elevato, ecc.). Ma se invece adotto il punto di vista intrinseco, posso dire che un nodo è un mondo nel quale un abitante ritiene di vivere su un filo, cioè dove può guardare solo avanti e indietro. Una superficie si può allora definire come un mondo nel quale un abitante ritiene di vivere al centro di un foglio di carta ; può guardare avanti, a sinistra, dietro, a destra e in tutte le direzioni intermedie, ma non in alto e in basso (cioè non potrà percepire la profondità dello spazio).
La teoria dei nodi conta una variante della definizione di superficie, quella di superficie con bordo : è un mondo nel quale un abitante ritiene di vivere al centro di un foglio di carta oppure su un lato di esso ; ci sono posizioni dalle quali può guardare avanti, a sinistra, dietro, a destra e in tutte le direzioni intermedie, altre in cui può guardare avanti, a sinistra, dietro e in tutte le direzioni intermedie (ma non a destra). Il bordo di una superficie è costituito dalle posizioni nelle quali la visuale è più limitata. In base alla definizione data, è evidente che il bordo di una superficie è un insieme di nodi, cioè un link. Come per i nodi, anche per le superfici posso scegliere di considerarne due (o più) equivalenti se sono deformabili l’una nell’altra, come accade per quelle a sinistra nella figura 14. Questo è il punto di vista estrinseco, ma posso anche adottare quello opposto, tornando ancora una volta ai nodi per introdurre l’idea.
- Note de bas de page 4 :
-
Precisiamo che un cilindro (un nastro al quale non viene impressa alcuna torsione) è una superficie orientabile, mentre il nastro di Möbius (ottenuto incollando tra loro, dopo una torsione, le estremità di una striscia di carta) è una superficie non orientabile. Un nastro di Möbius è una superficie monolatere, cioè composta di un solo lato. Detto diversamente, esso non si può colorare con due colori diversi. Si ha così la definizione : si chiamano orientabili le superfici di cui è possibile colorare i due lati opposti con due colori diversi. Le altre superfici (ne esistono di tantissimi tipi !) si chiamano non orientabili.
- Note de bas de page 5 :
-
In altre parole, riattacco ciò che ho tagliato lungo i bordi dei due sottospazi che trovo applicando questo tipo di “chirurgia”.
Per descrivere completamente i mondi dei nodi, non basta dire che in ogni punto si può solo andare avanti e indietro : è necessario compiere un’esplorazione completa. E lo stesso vale per il caso in esame : due superfici sono intrinsecamente uguali se un abitante dell’una e uno dell’altra possono percorrerle per intero, possono stare sempre in contatto comparando i loro spostamenti tramite dei sistemi di riferimento traducibili l’uno nell’altro, e verificando che in ogni momento le loro osservazioni siano le stesse. Intuitivamente questo significa che se applico una “chirurgia” a una superficie (per esempio tagliandola lungo un cerchio), poi la deformo e alla fine riattacco esattamente come avevo tagliato (ovviamente bisogna riattaccare lungo due circonferenze e seguendo un’orientazione4 fissata che indico con una freccia5 ; la superficie che ottengo alla fine è intrinsecamente uguale a quella che avevo all’inizio. Scopro così che le due superfici in basso e in alto nella figura 15 sono intrinsecamente uguali.
- Note de bas de page 6 :
-
La traduzione è difficile in italiano. L’idea è che esistono molti tipi di nodi il cui dispiegamento o svolgimento dà luogo a una superficie, o crea uno spazio il cui bordo è costituito dal nodo.
Un ultimo concetto importante che vogliamo introdurre è quello di nodi come bordi di superfici. Assegnato un nodo, chiamiamo knot-spanning6 una superficie il cui bordo sia costituito unicamente da tale nodo. Alcuni esempi sono mostrati nella figura 16. Si chiama superficie di Seifert un nodo che presenti le proprietà di essere knot-spanning e orientabile. A questo proposito, un risultato importante è il seguente : per ogni nodo ci sono infinite superfici knot-spanning, sia di Seifert che non orientabili ; tutte le infinite superfici di Seifert per un fissato nodo, determinano su di esso il medesimo (a meno di deformazione, naturalmente) riferimento, che dunque può essere chiamato riferimento caratteristico del nodo.
4. Fenomenologia, storia e cultura dei nodi
4.1. Nodi, intuizione dello spazio e percezione del mondo sensibile
Quanti sono a sapere che esistono dei termini del nostro linguaggio ordinario il cui significato spesso non coincide e può andare ben oltre l’uso che se ne fa nella vita di tutti i giorni ? È il caso dei due vocaboli correnti “nodo” e “buco”, che i bambini imparano a conoscere sin da quando muovono i primi passi. “Annodati i lacci delle scarpe”, “annodati il fiocchetto”, “fai un nodo stretto alla fune”, “attento ai buchi del cammino”, “non fare buchi sul quaderno su cui scrivi”, “infila bene lo spago nel buco”, ecc., sono tutte espressioni che ognuno di noi si è fatto ripetere come minimo due volte al giorno durante la sua infanzia e adolescenza. Anche se con un numero più o meno grande di varianti, si può nondimeno affermare con certezza che le stesse espressioni, con lo stesso significato o quantomeno con significati simili, siano esistite e ancora esistano in tutte le culture. Notiamo che tutte le espressioni precedenti traducono o invitano a eseguire un determinato movimento, il quale presuppone sia una certa attenzione sia una determinata azione, e in certi casi entrambe le cose. Notiamo ancora che l’azione inclusa in alcune delle espressioni precedenti richiede un’intuizione, seppur inconscia, dello spazio circostante e l’attitudine a saper eseguire uno o più gesti coordinati tra loro. All’inizio il bambino si fa un’idea dello spazio che lo circonda tramite l’intuizione di cui deve far prova per compiere dei gesti (delle mosse), come appunto “allacciarsi le scarpe”, “annodare la fune”, “ritagliare delle figure senza lasciare dei vuoti”, ecc. In altre parole, egli impara pian piano a conoscere lo spazio, non in modo astratto o applicando dei principi innati, ma piuttosto esplorando con il corpo e in particolare con le mani le possibilità inerenti allo spazio di eseguire determinati gesti in modo coerente ed effettivo, cioè in un modo che “fa senso”. Ciò significa che il senso è una costruzione plastica, un processo che si iscrive nell’esercizio dell’intuizione e nell’azione. In altre parole, esso emerge dalla nostra interazione con gli oggetti e gli esseri che “vivono” nello spazio ambiente, dalla presa di coscienza dei suoi limiti e delle sue impossibilità, e dalla conseguente scoperta delle sue proprietà e del suo modo di funzionamento.
L’intuizione dello spazio non è molto probabilmente una facoltà innata, o data a priori nell’intelletto (anche se si può, d’altra parte, pensare che l’intuizione, in quanto funzione fisiologica, conosca un certo sviluppo ontogenetico e filogenetico), ma è essenzialmente una capacità che si forma con e grazie all’azione, che si plasma man mano che esploriamo, mediante i nostri sistemi sensoriali (che formano un “tutto” che funge quando da “integratore” quando da “differenziatore”), l’interfaccia con lo spazio ambiente, più precisamente con gli oggetti e gli altri esseri che lo abitano. Tant’è vero che nelle prime fasi di questa interazione, e del nostro “essere al mondo”, la nostra intuizione dello spazio circostante (il “nostro spazio vitale”) è incerta, instabile e procede a tentoni : infatti, allacciamo male le scarpe, il nodo che abbiamo fatto allo spago si disfa subito dopo (ciò vuol dire che non era un “vero” nodo), non riusciamo a fare il salto o il passo giusto per evitare i buchi, ecc. Ciò significa che essa deve ancora crescere, autoregolarsi, trovare quelle proprietà e modalità giuste dei nostri movimenti e dei gesti con i quali manipoliamo gli oggetti, che consentono di capire come è fatto lo spazio, internamente ed esternamente, e quindi anche di capire come noi siamo costituiti rispetto allo spazio. É un'interazione reciproca : noi (il nostro corpo, i nostri movimenti, le nostre percezioni, il nostro « essere ») siamo ecologicamente e fenomenologicamente immersi nello spazio, con tutte le sue propretà e valenze, e nello stesso tempo ci plasma e forma la nostra specificità, la singolarità biologica e cognitiva di ognuno.
I nodi e i buchi hanno un significato “vitale” preminente. Con questo si intende che hanno un legame fondamentale con la vita, con il suo svilupparsi e riprodursi. Anche se la complessità segreta (uso qui l’aggettivo “segreto” per indicare l’altra faccia della complessità spontanea, non meccanica, auto-organizzata : ovvero la sua semplicità essenziale) di tale legame ci è sconosciuta, non ci può tuttavia sfuggire il fatto che i nodi e i buchi presentano una necessità evidente a più livelli della vita. L’anatomia del corpo umano deve molto del suo metabolismo e funzionamento globali al ruolo essenziale di certi orifizi e di certe cavità (l’orifizio rettale e quello dell’organo copulatore maschile, la cavità nasale e quella dell’orecchio), nonché a più strutture attorcigliate, ripiegate, annodate (si pensi agli avvolgimenti dell’intestino nello stomaco, o ai ripiegamenti della corteccia cerebrale nella scatola cranica ; di questi ultimi si comincia a capire il ruolo funzionale fondamentale che svolgono per lo sviluppo delle facoltà cognitive della nostra specie). Queste strutture anatomiche essenziali per il metabolismo cominciano a formarsi durante i primi stadi dell’embriogenesi e si stabilizzano poi nel corso dell’ontogenesi, cioè del processo che conduce all’individuazione degli esseri adulti. Ma nella filogenesi ritroviamo altri tipi di buchi e nodi, realizzati dalle diverse specie animali e vegetali a scopi diversi : nutrirsi, riprodursi, camuffarsi o accoppiarsi. I buchi e gli annodamenti sono utilizzati da svariate specie animali come altrettante strategie evolutive per affermarsi in seno a una comunità o sopravvivere di fronte al più forte, ma anche come elemento ludico e strumento di comunicazione.
4.2. I nodi : modello di un linguaggio polisemico non verbale
- Note de bas de page 7 :
-
Nell’accezione di legami assolutamente vincolanti, contraria al senso proprio dell’oggetto nodo che è quello di avvicinare cose lontane, stabilire connessioni, formare intrecci creativi.
- Note de bas de page 8 :
-
Cfr. L. Boi, “Topological knot theory and macroscopic physics”, in Encyclopedia of Mathematical Physics, J.-P. Françoise, G. Naber, T. S. Tsun (eds.), Elsevier, Oxford, 2006, pp. 271-277.
Il nodo ha rivestito sempre una grande rilevanza nelle varie culture e nelle pratiche antropologiche e simboliche di ogni epoca, tanto da immortalarlo nelle incisioni rupestri, da inserirlo in contesti rituali, da adottarlo come caratteristica specifica di taluni ordini monastici, da evidenziarlo in molte opere d’arte, in cui non è mai posto in modo casuale o decorativo. Per gli Egizi, il nodo era segno di vita. Buddha insegna che “disfare i nodi del cuore”7 è il processo che porta alla liberazione, all’elevazione dell’essere, il passaggio ad uno stato superiore, e i nodi fatti in un certo ordine possono essere sciolti solo nell’ordine inverso, con un metodo rigoroso che è une regola del Tantrismo. Il nodo di bambù cinese è una successione verticale che segna una gerarchia di stati lungo l’asse Cielo-Terra, e ha similitudini con il concetto dei chakra tantrici, la “gerarchia” di stati lungo il nostro asse corpo-mente, materiale-spirituale, terrestre-celeste : sciogliere questi “nodi” è vitale per far fluire l’energia vitale nell’uomo e portarlo alla sua libertà. I nove nodi dei taoisti hanno il potere di captare la realtà, di far condensare stati ed elementi. Notiamo, a questo proposito, che le ricerche recenti sulla dinamica dei fluidi hanno evidenziato l’importanza dei nodi e di certi invarianti ad esse associati per stabilizzare svariate strutture fisiche macroscopiche e minimizzare la dissipazione di energia.8
Famoso è il Nodo di Gordio, un misero contadino che divenne re di Frigia, il cui timone del proprio carro fu legato da suo figlio Mida con un nodo talmente complicato che nessuno era in grado di scioglierlo e, secondo l’oracolo di Telmisso (antica capitale della Frigia), l’impero d’Assia sarebbe andato nelle mani di colui che ci sarebbe riuscito. Dopo che molti ebbero tentato e fallito, Alessandro Magno giunse a Frigia nel palazzo di Gordio (nel IV secolo a.C.) e dopo aver tentato di sciogliere il nodo lo tagliò a metà con un colpo della sua spada ed ebbe il regno ma in modo effimero poiché lo perse poco dopo. La “soluzione alessandrina” fa riferimento nella mitologia a una falsa soluzione : il nodo si scioglie ma non si taglia ; tagliandolo se ne distruggono la complessità e realtà invisibili che esso racchiude. Il Nodo di Salomone è uno dei simboli più antichi e riprodotti in ogni tempo dall’uomo : basti pensare che se ne conoscono esemplari tracciati in maniera approssimativa in epoca preistorica, in incisioni rupestri. Tuttavia la sua diffusione si sviluppa soprattutto con le culture euro-asiatiche, africane e amerindie, e raggiunge il suo apice nella cultura celtica, fortemente basata sui temi dei nodi, degli intrecci e delle figure ondulate. Il Nodo di Salomone era costituito da complicati intrecci geometrici che disperdevano stregonerie e malefici.
Presso l’impero Inca, i nodi (nella loro lingua quipu o Khipu) erano parte integrante della vita quotidiana e rappresentavano un vero e proprio sistema di scrittura e contabilità. Con questo sistema, gli Inca detenevano archivi, creavano calendari, effettuavano censimenti, campionamenti : i nodi erano mezzi di trasmissione di messaggi, quindi strumenti importantissimi di comunicazione. Un sistema “tridimensionale”, oltre le due dimensioni della nostra scrittura. Il marchingegno era costituito da una cordicella orizzontale, di cotone, raramente di lana, alla quale venivano attaccate altre cordicelle annodate di diverso colore, che a loro volta potevano avere ulteriori funicelle annodate. La contabilità dell’impero era affidata ai quipu-kamaya, o quipucamayoc (contador), “i maestri delle cordicelle a nodi”. E si pensa che solo loro conoscessero il significato di ogni singolo quipu, che è unico.
Secondo alcuni studiosi, il quipu era basato sul sistema decimale, in cui il tipo di realizzazione fisica del nodo assumeva una valenza ben precisa : un nodo semplice corrispondeva all’unità, un doppio alle decine e un triplo alle centinaia. Per scrivere la cifra 1705, ad esempio, si registrava un nodo nella posizione delle migliaia, 7 nodi in quelle delle centinaia, nessuna tra quelle delle decine e 1 nodo riannodato cinque volte, nella posizione delle unità. Quest’ultimo era un caso speciale, che serviva da punto di riferimento : lo spazio delle unità non conteneva mai più di un singolo nodo, a forma di 8 per indicare 1 e con un cappio in più per ogni somma da 2 a 9. Un’altra caratteristica appare chiara. Le cordicelle supplementari attaccate alla stringa annodata indicavano probabilmente una serie di informazioni secondarie, come ad esempio il numero di uomini in un dato gruppo di contraenti. Il colore della cordicella era fondamentale, poiché contraddistingueva il soggetto o il tipo di prodotto cui si riferiva il conteggio (ad esempio la cordicella gialla era riservata al mais). Le stringhe o cordicelle annodate avevano diversa lunghezza, raggruppate in diversi modi, e i nodi potevano presentare una varietà di posizioni strabiliante : da qui la difficoltà nella decifrazione dei quipu.
- Note de bas de page 9 :
-
Cfr. G. Urton, Signs of the Inka Khipu: Binary Coding in the Andean Knotted-String Records, University of Texas Press, Austin, 2003.
Recentemente, lo studioso Gary Urton ha studiato oltre seicento khipu conservati nei vari musei (molti sono dispersi, altri in collezioni private), e ha asserito che in realtà il quipu è da intendersi come un sistema di comunicazione a base binaria9. Tale sistema sarebbe una sorta di linguaggio (un codice complesso) basato su sette possibilità, che combinate in un determinato numero di modi fornirebbero 1536 informazioni diverse, un sistema tutt’altro che elementare. È lecito supporre che i quipu dovevano celare anche un significato non solo “numerico” ma artistico e letterario, nel quadro di una certa visione cosmogonica dell’universo di natura ciclica e pertanto illimitata. Probabilmente esistono anche “traduzioni”, trascritte in lingua comprensibile, di quei “libri annodati”. Molti elementi risalenti a quell’epoca lasciano intendere che la posizione di nodi e la direzione dell’annodatura possano fornire preziosi indizi per la decodifica del significato. Si può infatti notare, ad esempio, che alcune stringhe assumono forme spiraliformi, altre sono annodate in senso antiorario, altre in senso orario.
È probabile che i Khipu avessero una doppia valenza : quella per le attività quotidiane, di uso comune, e quella riservata alle caste sacerdotali, poiché pare che il gesuita Joan Anello Olivia abbia scritto nel “Monumenta Piruana” codeste parole : “I quipu che serba i segreti della religione e delle caste ha una chiave di compilazione e composizione differente. (…) Grazie alla dimestichezza che essi hanno con i fili, questi, li riavvolgono in nodi di differenti colori sino a formare il concetto desiderato”. Pare che nel racconto, Oliva descrivesse anche l’aspetto sillabico di un quipu che gli era stato mostrato e che raffigurava il Creatore Pachacamac, specificando che ad ogni sillaba corrispondeva uno specifico nodo, in una data posizione, ecc. Un messaggio cifrato, praticamente ! Questa “arte combinatoria” dei nodi venne ritenuta (pur non comprendendola) idolatria e la stragrande maggioranza dei nodi venne data al rogo dai conquistatori e evangelizzatori cristiani.
Nel Rinascimento e poi nell’epoca moderna saranno molti gli artisti, matematici e naturalisti che dedicheranno un’attenzione e una ricerca particolari alle qualità e ai significati dei nodi, trasformandoli, in certi casi, in un vero linguaggio necessario per conoscere e spiegare le proprietà delle cose e le strutture del mondo (Albrecht Dürer, Leonardo da Vinci).
5. Geometria proiettiva e prospettiva : l’invenzione dello spazio pittorico
La geometria proiettiva è la parte della geometria che dà forma ai concetti intuitivi di prospettiva e di orizzonte. Definisce e studia gli enti geometrici usuali (punti, rette, …) senza utilizzare misure o confronto di lunghezze. La geometria proiettiva può essere pensata informalmente come la geometria che nasce dal collocare il proprio occhio in un punto dello spazio, così che ogni linea che intersechi l’“occhio” appaia solo come un punto. Le grandezze degli oggetti non sono direttamente quantificabili (perché guardando il mondo con un occhio soltanto non abbiamo informazioni sulla profondità) e l’orizzonte è considerato parte integrante dello spazio. Come conseguenza, nella geometria piana proiettiva due rette si intersecano sempre (non sono mai parallele). L’origine della geometria proiettiva si può far risalire ai lavori dell’artista e matematico francese Girard Desargues (1591-1666), che cercava una via alternativa per il disegno in prospettiva, che generalizzasse l’uso dei “punti di fuga” ed includesse il caso in cui questi sono infinitamente lontani. Egli concepiva la geometria proiettiva come un sistema geometrico più generale rispetto alla geometria euclidea che la includeva al suo interno. Il passaggio dalla geometria analitica (di Cartesio) a quella proiettiva (sviluppata nella prima metà del XIX secolo da Gaspard Monge, Jean-Victor Poncelet, Jakob Steiner et Jules Plücker, poi nella seconda metà dell’Ottocento dalla scuola italiana di geometria algebrica) si effettuò sostituendo le usuali coordinate cartesiane con delle nuove coordinate, dette coordinate omogenee. Una coppia di punti antipodali sulla sfera S2 individua univocamente una retta nello spazio tridimensionale passante per l’origine. Tale retta può essere individuata da equazioni parametriche della forma : x = at, y = bt, z = ct, t ∈ R (dove i coefficienti a, b e c non sono tutti nulli) e dalla famiglia di infinite equazioni che si ottengono moltiplicando tutti i coefficienti par uno stesso fattore non nullo. Questo significa che il piano proiettivo può essere rappresentato da terne di coefficienti (a, b, c) non nulle identificando tra loro le terne che differiscono per una costante di proporzionalità. Questo equivale a considerare l’insieme quoziente di R3\{0} rispetto alla relazione di equivalenza (a, b, c) ∼ (a’, b’, c’) ⇔ a/a’ = b/’ = c/c’. Tramite queste coordinate, lo spazio (ad esempio, il piano) si arricchì di alcuni “punti all’infinito” che la geometria proiettiva considerava punti a tutti gli effetti, indistinguibili dai punti “finiti” (da cui il carattere omogeneo del nuovo spazio, in cui tutti i punti hanno lo stesso ruolo).
La geometria proiettiva includeva come una sua proprietà basilare quella dell’incidenza tra due rette qualunque nel piano : due rette distinte L e M nel piano proiettivo si intersecano sempre in esattamente un punto P. Contrariamente alla geometria euclidea o analitica, in quella proiettiva non esistono rette parallele. Il caso “eccezionale” delle rette parallele viene eliminato aggiungendo al piano i “punti all’infinito”. Questi nuovi punti formano anch’essi una retta, detta “retta all’infinito” o “impropria”, o anche “orizzonte”. La teoria considera quindi la “retta all’infinito” come una retta qualsiasi, indistinta dalle altre. Grazie all’aggiunta dei punti all’infinito, e all’eliminazione dei fenomeni di parallelismo, molti teoremi classici assumono nella geometria proiettiva una forma più semplice, più essenziale. Ad esempio, la geometria proiettiva fornisce una descrizione breve ed elegante delle sezioni coniche : iperbole, parabola ed ellisse altro non sono che la “stessa conica” nel piano proiettivo, e le differenze fra questi tre enti dipendono soltanto da come questo oggetto interseca la retta all’infinito : l’iperbole la interseca in due punti, la parabola in uno solo, l’ellisse in nessuno.
La geometria proiettiva ha profondamente rinnovato il linguaggio della geometria euclidea, in particolare allargando e pluralizzando il significato dei suoi enti e stabilendo delle nuove relazioni essenziali tra i suoi oggetti. Limitiamoci a citare qualche esempio. Il piano proiettivo è un’estensione del piano euclideo a cui viene aggiunta una “retta impropria” posizionata idealmente all’infinito e atta a circoscriverlo. Esteso in questo modo il piano diventa uno spazio compatto in cui anche le rette parallele si incontrano in un unico punto e tale punto di intersezione è idealmente collocato sulla “retta impropria” (o immaginaria). La retta impropria può essere visualizzata come la retta che si vede all’orizzonte quando un piano euclideo viene rappresentato in prospettiva oppure può essere pensata come una circonferenza infinitamente lontana che delimita tutto il piano euclideo e i cui punti antipodali sono identificati in maniera tale che le rette parallele ad una stessa direzione abbiano un unico punto di intersezione su di essa. Il piano proiettivo reale, P2, è lo spazio di linee in R3 passante per l’origine. È una varietà differenziabile non orientabile 2-dimensionale, vale a dire una superficie che non può essere immersa senza auto-intersecarsi nel nostro spazio 3-dimensionale. Essa ha caratteristica di Eulero pari a 1 e quindi genere unitario.
Un modello di piano proiettivo può essere definito matematicamente in vari modi che forniscono strutture isomorfe. Un modello di piano proiettivo si ha considerando la sfera S2 immersa nello spazio euclideo tridimensionale in cui : (a) definiamo punti proiettivi del piano proiettivo le coppie di punti antipodali sulla sfera ; (b) definiamo rette proiettive del piano proiettivo tutti i cerchi massimi che giacciono sulla sfera. Questo equivale a considerare sulla sfera la relazione di equivalenza ∼ che identifica i punti x ∼ y : ⟺ x = y oppure x = –y, e definire il piano proiettivo come lo spazio topologico quoziente P2 : = S2 / ∼. È possibile definire una applicazione che manda il piano proiettivo P2 privato di una retta nel piano euclideo in modo tale da mandare rette proiettive in rette euclidee. A tale scopo consideriamo nello spazio tridimensionale il piano P tangente alla sfera S2 nel “polo sud”. Possiamo associare alle copie di punti antipodali sulla sfera (che sono punti del piano proiettivo) un punto del piano P individuato dall’intersezione del piano con la retta congiungente i due punti antipodali. Intuitivamente è come se stessimo guardando l’ombra prodotta sul piano da questa coppia di punti quando una sorgente di luce è disposta nel centro della sfera. I cerchi massimi sulla sfera (corrispondenti a rette proiettive) vengono mandate tutte in rette sul piano P. Questa applicazione manda tutti i punti del piano proiettivo sul piano P fatta eccezione per i punti appartenenti al cerchio massimo parallelo al piano (che in qualche senso vengono mandati all’infinito). Se omettiamo tale cerchio dal dominio, l’applicazione così definita è una corrispondenza biunivoca che fa corrispondere rette del piano a rette proiettive sul piano proiettivo. Questa costruzione mostra in che modo il piano proiettivo possa essere visto come un’estensione del piano euclideo. La topologia naturale per il piano proiettivo P2 definito come una sfera quozientata si ha considerando la topologia quoziente della sfera rispetto alla relazione di equivalenza in essa definita. Lo stesso spazio topologico (a meno di omeomorfismi) può essere ottenuto considerando un quadrato ed incollando i lati opposti nei versi contrari (ovvero identificando tra loro i punti antipodali rispetto al centro del quadrato). Topologicamente, il piano proiettivo è uno spazio compatto, connesso, localmente omeomorfo al piano euclideo R2, e non orientabile, ciò significa che non può essere ottenuto come superficie immersa nello spazio euclideo tridimensionale senza autointersezioni. Il rivestimento universale del piano proiettivo è la mappa S2 → P2 indotta dalla relazione d’equivalenza antipodale. Il gruppo fondamentale del piano proiettivo è dato dal gruppo di due elementi Z2. La sua caratteristica di Eulero è 2, e il suo genere è 1.
Le stesse proprietà geometriche e topologiche sopra indicate valgono, mutatis mutandis, per lo spazio proiettivo. Si può definire lo spazio proiettivo n-dimensionale come l’unione di Rn e di tutti i suoi “punti all’infinito”, oppure, in modo più naturale, come l’insieme delle rette in Rn+1 passanti per l’origine. Intuitivamente, lo spazio proiettivo a n dimensioni è lo spazio che vede un occhio posizionato nell’origine. Questa definizione esprime chiaramente le relazioni con la prospettiva.
5.1. La complessità pittorica del reale nell’opera di Piero della Francesca
La prospettiva è un insieme di proposizioni e di procedimenti di carattere geometrico che consentono di costruire l’immagine di una figura dello spazio su un piano, proiettando la stessa da un centro di proiezione posto a distanza finita. Si tratta quindi di una proiezione centrale, o conica. La specificazione è utile per distinguerla dalla prospettiva parallela, modo alternativo, anche se non di uso corrente, di chiamare le assonometrie. Gli elementi fondamentali necessari alla costruzione della prospettiva di una figura obiettiva, che si suppone data nello spazio, sono, come per ogni metodo di rappresentazione, il piano di proiezione, a cui si dà in genere il nome specifico di “quadro”, e il centro di proiezione, chiamato normalmente “punto di vista” o “centro di vista”. Per procedere operativamente nel disegno occorre anche fissare la posizione di alcuni elementi di riferimento, di seguito elencati. Un piano orizzontale, detto “piano geometrale” che, intersecando il quadro, fornisce la “linea di terra”, luogo delle tracce di tutte le rette appartenenti allo stesso piano geometrale. La proiezione ortogonale del punto di vista sul piano geometrale individua il cosiddetto “punto di stazione”, mentre la proiezione ortogonale dello stesso punto di vista sul quadro determina il “punto principale”. L’intersezione del quadro con un piano orizzontale passante per il centro di vista è una retta denominata “linea d’orizzonte”, parallela alla linea di terra e luogo delle fughe di tutte le rette orizzontali, ovvero retta di fuga di tutti i piani paralleli a quello geometrale. In alcuni casi può essere utile tracciare il “cerchio di distanza”, che ha il centro nel punto principale, raggio uguale alla distanza del centro di vista dal quadro, ed è il luogo geometrico delle fughe di tutte le rette inclinate di 45° rispetto al quadro. È inoltre necessario disporre delle proiezioni ortogonali della figura obiettiva, la cui vista dall’alto, o pianta, viene di solito riportata sul piano di terra.
Dal punto di vista linguistico, il vocabolo “prospettiva” è la forma femminile di “prospettivo”, derivante a sua volta dal latino tardo “prospectivus”, che assicura la vista. Nel campo degli studi ottici medievali la perspectiva indicava l’ottica stessa (perspectiva naturalis), intesa come percezione visiva. In particolare indicava la pratica per misurare le distanze e le lunghezze tramite un rilevamento indiretto. Nel tardo Rinascimento, al problema della prospettiva e della percezione visiva furono interessati in modo particolare gli artisti, che a volte erano delle personalità provviste di solide cognizioni matematiche. E nel caso di Piero della Francesca (1416-1417 circa – 1492) si ha un vero cultore della materia, tanto da poter essere definito un valente geometra. Le sue opere sono mirabilmente sospese tra arte, geometria e un complesso sistema di lettura a più livelli, dove confluiscono complesse questioni teologiche, filosofiche e politiche. Riuscì ad armonizzare, nella vita quanto nelle opere, i valori intellettuali e spirituali del suo tempo, congiungendo molteplici influssi e dialogando tra tradizione e modernità, tra razionalità ed estetica. La sua opera fece da cerniera tra la prospettiva geometrica di Brunelleschi, la plasticità di Masaccio e l’arte della luce di Fra Angelico. Altre caratteristiche fondamentali della sua espressione poetica sono l’essenzialismo geometrico sia delle composizioni che dei volumi, l’altissima spiritualità dei gesti, l’attenzione alla verità umana. Piero della Francesca parlerà di prospettiva come di vera scientia. La riscoperta della cultura classica, e in particolare di quella scientifica, e l’importanza conoscitiva, estetica e persino etica attribuita alla geometria, considerata allo stesso tempo una scienza e un’arte, ha avuto un ruolo centrale nella svolta culturale che ha caratterizzato l’epoca rinascimentale. Euclide e i suoi Elementi, variamente tradotti e commentati, diventarono un modello a cui riferirsi. Gli affreschi posteri della Flagellazione di Cristo e della Sacra conversazione portano fortemente i caratteri della visione geometrica di Piero della Francesca.
Piero della Francesca è riconosciuto tra i più grandi geometri e artisti del Rinascimento. La sua opera, Flagellazione di Cristo, rappresenta l’esempio più interessante dell’applicazione delle regole prospettiche moderne da parte di Piero. La lettura del modello prospettico utilizzato, tuttavia, risulta difficile e controversa per la singolarità dell’impostazione. L’interpretazione del dipinto è necessariamente complessa, poiché in esso le dimensioni spaziale e temporale sono profondamente legate : l’organizzazione spaziale multipla e allo stesso tempo convergente della scena evoca una certa memoria storica di eventi connessi anche se forse non simultanei ; e questa memoria storica che si dispiega nel tempo conferisce agli eventi immersi nello spazio del dipinto una contiguità e una connessione fondamentali.
In termini più descrittivi, se infatti è facile riconoscere la scena della flagellazione di Cristo sotto la loggia a sinistra, non è affatto semplice conciliare con essa la presenza dei tre personaggi in primo piano a destra, che la loro posizione spaziale prominente suggerisce presenti con funzione significante all’interno della rappresentazione. Nella Flagellazione la rievocazione « storica » della vicenda di Cristo è rappresentata all’interno di una loggia terrena, aperta frontalmente e con i personaggi in costume « all’antica », mentre un abito inconfondibilmente moderno riveste i tre uomini in primo piano, che occupano la porzione destra del riquadro, fuori dal contesto spaziale della flagellazione, anche se visivamente in continuità con esso. E tale unità è sottolineata nella gabbia architettonica prospettica, che struttura in maniera organica l’intero spazio. Nel portico le figure sono piccole, ma ben commisurate alla struttura architettonica e si collegano proporzionalmente fra loro anche grazie al disegno quadrettato del pavimento in forma di tassellazione regolare. L’uso della luce, poi, è sapiente e sofisticato, tanto da aver suggerito la presenza di una sorgente luminosa sulla destra del portico e a fianco del Cristo alla colonna, che ne viene investito direttamente insieme al soffitto sovrastante, acquistando così una salienza marcata nel contesto del dipinto.
- Note de bas de page 10 :
-
Alhazen, o Abu Ali al-Hasan Ibn al-Hasan Ibn al-Haytham (Bassora, 965-Il Cairo, 1038), è stato un medico, filosofo, matematico, fisico ed astronomo arabo. Considerato uno dei più importanti e geniali scienziati del mondo islamico. Da taluni è considerato l’iniziatore dell’ottica moderna.
- Note de bas de page 11 :
-
Cfr. R. Wittkower, B.A.R. Carter, “The Perspective of Piero della Francesca’s Flagellation”, in Journal of the Warburg and Coutauld Institutes, XVI (1953), pp. 292-302. Sull’argomento si veda altresì J. V. Field, Piero della Francesca. A Matematician’s Art, Yale University Press, New Haven, 2005 (in particolare le pp. 174-181).
Piero non affronta esplicitamente il problema della luce (e del colore) nel suo trattato De prospectiva pingendi, ma la prova del suo interesse per l’argomento è rintracciabile nelle opere pittoriche ; inoltre può avere ricevuto uno stimolo ulteriore della conoscenza delle teorie ottiche di Alhazen10, che trattano della trasmissione rettilinea della luce. Come accertato dallo schema ricostruttivo dell’impianto prospettico elaborato da Carter e Wittkover11, l’insieme spaziale è stato accuratamente calcolato fin nella posizione dei particolari e il punto di fuga risulta centrico e collocato verso il basso, fra lo stipite destro della porta posta dietro la figura di Cristo e l’infilata delle colonne che delimitano il loggiato sulla destra. Di conseguenza alcuni studiosi hanno voluto vedere in questa opera un punto di arrivo nell’elaborazione prospettica di Piero, quasi una dimostrazione pratica della riflessione teorica sul problema della resa spaziale, con conseguenti riflessi sia sulla datazione del dipinto che del De prospectiva pingendi. Se la soluzione di collocare due scene distinte in contiguità spaziale può derivare dalla distribuzione dei loci deputati alla scenografia del teatro medievale, Piero non si limita ad applicare tale tradizione acriticamente. I due luoghi, infatti, sono volutamente differenziati anche nella resa prospettica. Nella Flagellazione la gabbia grafica della loggia è lucidamente offerta alla vista con le linee convergenti dell’architettura e della scacchiera pavimentale, che guidano l’occhio dell’osservatore ad una comprensione razionalmente calcolabile dello spazio, tanto che è risultato possibile ricostruire la planimetria dell’ambiente raffigurato. Se dal punto di vista geometrico la proiezione può essere definita frontale, l’effetto ottico tende invece a spostare il centro dell’attenzione visiva verso destra a causa dell’incombere dei tre personaggi in primo piano, collocati contro uno spazio definito da strutture architettoniche in deciso scorcio verso la profondità. In questa parte della raffigurazione la lettura spaziale appare più difficoltosa, perché Piero ha volutamente coperto molti punti di riferimento geometrico, cosicché la reale distanza fra i tre personaggi in primo piano e la parete a rombi bicolori del fondo è più intuibile che misurabile.
Fig. 17. Piero della Francesca, Flagellazione di Cristo, ca. 1459, Urbino, Galleria Nazionale.
Tra i trattati scientifici di questo importante pittore, ci sono ben tre opere di matematica : il De corporibus regularibus, il Trattato d’abaco e il De prospectiva pingendi. Il De Prospectiva pingendi è stato il primo vero organico trattato compilato sulla scienza prospettica del Rinascimento e tanta è la sua validità che, per un lungo arco di tempo, sarebbe rimasto come esempio e fonte per successivi autori di opere di prospettiva. Fu scritto verso il 1475. Articolato in tre libri, questo trattato sviluppa in senso nettamente matematico i problemi della rappresentazione prospettica offrendo esempi operativi non solo riferiti a complesse forme geometriche e architettoniche, ma a qualsiasi forma naturale. Il primo libro, di geometria piana, ha propositi didattici dimostrati da nitidi e precisi disegni. Il secondo, di geometria solida, verte sulla rappresentazione prospettica dei solidi. Il terzo libro determina obiettivamente l’immagine prospettica di oggetti complessi. Con la prospettiva elaborata da Piero della Francesca nelle sue opere, i nuovi criteri di rappresentazione del reale sostituiscono le immagini statiche della pittura duecentesca e ricercano nella geometria delle forme e dei rapporti prospettici il rapporto con le cose. Le figure astratte e metafisiche di Piero della Francesca dimostrano che la prospettiva non è necessaria soltanto a quelle culture che, tendendo al realismo, affidano all’immagine il compito di riprodurre la realtà.
Le opere artistiche del pittore di Borgo San Sepolcro evidenziano la tendenza dell’uomo del Quattrocento a indagare, a studiare la realtà in cui vive, che lo porta a definire le leggi della prospettiva, a considerare le immagini nel loro volume, nelle loro proporzioni e relazioni. Nell’antichità classica il ruolo della simmetria come principio ispiratore nella concezione del mondo fisico veniva accentuato dalla rarità di figure solide analoghe ai poligoni regolari. Mentre infatti nel piano abbiamo un’infinità numerabile di poligoni regolari corrispondenti ai gruppi finiti di rotazioni, nello spazio tridimensionale si possono realizzare soltanto cinque poliedri regolari : il cubo, il tetraedro, l’ottaedro, il dodecaedro e l’icosaedro. Questi poliedri regolari sono tradizionalmente chiamati solidi platonici per il ruolo fondamentale che giocano nella cosmogonia elaborata da Platone. Costui, nel suo dialogo, Timeo, associa il tetraedro, l’ottaedro, il cubo, e l’icosaedro rispettivamente a quelli che erano allora ritenuti i quattro elementi fondamentali : fuoco, aria, terra e acqua. Il dodecaedro, non realizzabile unendo opportunamente triangoli (come invece avviene per gli altri poliedri citati), veniva invece associato all’immagine del cosmo intero, realizzando la cosiddetta quinta essenza. Questa identificazione suggerisce un’immagine di perfezione che indubbiamente nasce dal fatto che il dodecaedro approssima più degli altri poliedri regolari la sfera.
- Note de bas de page 12 :
-
I numeri di Betti consentono di descrivere la connettività delle superfici e degli spazi a un numero qualsiasi di dimensioni. Essi permettono di capire le caratteristiche di un qualsiasi oggetto geometrico, in particolare il numero di componenti (o regioni) che lo compongono, o il numero di buchi che possiede, i quali specificano il suo grado di disconnettività. Un oggetto geometrico ha un numero di Betti superiore di 1 rispetto al suo numero di dimensioni ; si tratta di una proprietà fondamentale, intrinseca. Così, gli oggetti a 1 dimensione come il cerchio hanno numero di Betti 2, b2, gli oggetti bidimensionali come le superfici delle palle, le ciambelle con due buchi e i bretzels hanno numero di Betti 3, b3. Intuitivamente, l’ennesimo numero di Betti determina la connettività n-dimensionale o il numero di buchi di un oggetto geometrico a n dimensioni (superficie, spazio, …)
- Note de bas de page 13 :
-
I coefficienti di torsione misurano il tipo e il grado di torsione di un oggetto geometrico. Una banda circolare la si può torcere fino a che diventi un nastro di Möbius, che è un oggetto geometrico provvisto di torsione. Per convincersene, basta percorrere tutto il bordo del nastro, e alla fine ci si renderà conto che ci sono voluti due giri per percorrere l’intero bordo. Molti oggetti materiali così come molti spazi che hanno un legame non casuale con il mondo fisico sono provvisti di torsione. Anche un cilindro avvitato su sé stesso o una treccia sono degli oggetti geometrici dotati di torsione. In certe forme di danza e di ginnastica o in certi sport come il tuffo, il movimento rotatorio del corpo sul suo asse longitudinale è un esempio particolarmente interessante di torsione. La geometria e la dinamica della torsione è fondamentale per spiegare una grande varietà di fenomeni fisici, biologici e psichici. Esiste una classe molto importante di spazi, detti “spazi con torsione” (o anche “spazi di Cartan” dal nome del suo inventore), che giocano un ruolo fondamentale nella modellazione dei fenomeni fisici, sia gravitazionali che quantistici. La torsione di certe strutture macromolecolari nella cellula ha un importante significato funzionale. Ai gradi di torsione di un oggetto fisico (per esempio di un corpo) è possibile anche associare delle valenze di senso (o delle variazioni semantiche) che ne indicano i tassi di trasformazione rispetto a una finalità o a un’intenzione.
Oggi però sappiamo, grazie innanzitutto all’intuizione di Poincaré e ad altre ingegnose costruzioni suggerite da diversi matematici (Max Dehn, James Waddell Alexander, Helmut Kneser), che lo spazio dodecaedrico di Poincaré, detto anche “sfera di omologia”, non può essere trasformata topologicamente (cioè per deformazione elastica) in una sfera, e ciò nonostante esso possegga gli stessi “numeri di Betti”12 e gli stessi “coefficienti di torsione”13 di una sfera (lo spazio dodecaedrico 3-dimensionale di Poincaré è uno spazio senza buchi e privo di torsione). Si tratta di un problema topologico profondo e complesso che non esporremo qui.
Figura 18. Illustrazione artistica di un tipo di torsione (Jorge E. Eielson, Torsione, 1994).
Si tratta di una corda colorata avvolta su se stessa. Una corda avvolta mediante torsione acquista energia e perde massa. Il torcere un oggetto malleabile ha come effetto di trasformarlo in qualcosa d’altro, e la forza con la quale si effettua tale operazione, gli conferisce una certa quantità di energia che si conserva come risultato della deformazione. Questa semplice esperienza mostra che massa e energia non sono equivalenti, come tutta la fisica relativista ci ha insegnato. La torsione è fondamentale per la vita, a cominciare dal suo livello molecolare. Il DNA è avvolto in forma di doppia elica, nella quale entrambe ruotano attorno ad un asse. Un ulteriore ripiegamento o una torsione di tale asse su se stesso producono un superavvolgimento del DNA. Il superavvolgimento del DNA è, in genere, una manifestazione della tensione strutturale, mentre se non esiste alcun ripiegamento si dice che il DNA si trova in uno stato rilassato. Una modesta torsione provoca un grosso avvolgimento ; una grossa torsione non modifica l’avvolgimento della catena di DNA. Il superavvolgimento può prendere forme differenti. L’immagine della figura illustra il superavvolgimento a solenoide, cha ha la forma di stretti avvolgimenti levogiri attorno ad una struttura immaginaria a forma di tubo. Come si intuisce, questa tensione, che agisce come una forza dinamica, può produrre un cambiamento di forma della doppia elica, e questa nuova forma modifica la funzionalità delle strutture macromolecolari. La torsione presenta degli aspetti straordinari anche nel mondo vegetale, dove essa è da ricollegarsi al fenomeno dell’aptotropismo (dal greco apto, tocco e trepo, volgo). Se per esempio con un bastoncino tocchiamo il viticcio di una zucca, osserviamo poco dopo che il viticcio si curva e tende ad avvolgersi dalla parte dalla quale è stato toccato. Questo avviene per la capacità che hanno molte piante di percepire un contatto e reagire. Molto evidente è la sensibilità al tatto delle piante rampicanti che sono munite di viticci i quali sono in grado si avvolgersi a dei sostegni. La torsione è tra i gesti primordiali dell’immaginazione matematica, e infatti essa consente di generare nuove curve, superfici e varietà contenenti diversi tipi di singolarità e nuove proprietà geometriche e topologiche.
La fortuna dei solidi platonici nell’immaginario scientifico della cultura occidentale è stata enorme, ed è forse connessa ad un punto di vista filosofico che riteneva di poter penetrare profondamente nei segreti della creazione guardando a questi simulacri euclidei delle idee di Platone. Arte e scienza si intrecciano in maniera profonda nel Libellus de corporibus regularibus di Piero della Francesca. L’idea che ispira un tale progetto è di una profonda originalità e singolare modernità nel senso che si vuole sostenere (siamo alla fine del XV secolo), contro i pregiudizi di certi teologi, scienziati e umanisti, come la scienza non sia mera astrazione o pura tecnica, ma anche e soprattutto forma di conoscenza e arte di creazione.
Ci pare interessante citare qualche passaggio di Yves Bonnefoy sul significato della prospettiva e dell’opera di Piero della Francesca :
- Note de bas de page 14 :
-
Yves Bonnefoy, L’arrière-pays, Gallimard, 2005, pp. 167-169.
Urbin, ce n’est seulement le musée où la surprenante prédelle de Paolo Uccello attire dans son abîme, c’est le palais dont l’architecture savante est l’émanation même de l’art de Piero della Francesca. Et réfléchir à celui qui, s’il en fut un, a bien été le maître des nombres conduit à mieux comprendre pourquoi il chercha, et si bien, à produire de l’harmonie dans les formes ; et comment le nombre qui n’est qu’un rêve, l’incessant rêve du platonisme à travers l’histoire, peut tout de même aider à se dégager du rêve, sans rien oublier pourtant, dans cette expérience nouvelle et soudain lucide, des aspirations qui avaient donné vie à ce grand mirage. Ce qui lui vaut d’être maintenant un miroir de l’existence comme elle est, non comme on la veut : un moyen pour la vérité. Comment la beauté des formes peut-elle échapper aux pièges de l’imagination désirante ? Ce fut, au cours du XVe siècle, à l’aide de la « prospectiva pingendi » ou, plus précisément, de la façon dont elle fut employée par certains artistes dans les premiers temps de son invention. La perspective comme de grands Toscans l’ont élaborée au Quattrocento, Dieu sait si on peut la mettre au service du fantastique, de l’irréel, du rêve : et ce fut vite le cas… (…) La perspective et son projet d’origine se soucie moins de la maîtrise abstraite de l’espace que de rétablir un rapport de la personne à son lieu naturel – et à son corps – qu’avait étouffé depuis trop longtemps la pensée purement verbale des théologiens médiévaux. Elle est une incitation à sortir de cette nuit-là, et un moyen pour le faire : son apport, son vrai apport, n’étant pas l’étendue mais la lumière du jour comme il se lèvera plus limpide dans des lieux de plus de raison. La lumière de ces matins d’été où le monde semble s’offrir.14
- Note de bas de page 15 :
-
Piero nel De prospectiva pingendi tratta sostanzialmente soltanto della prospettiva geometrica, e cioè della rappresentazione spaziale configurata attraverso il disegno e in cui gli scorci delle forme verso la profondità sono razionalmente calcolabili. Nell’attività pittorica, tuttavia, egli usa almeno altri due modelli di rappresentazione prospettica : l’uno procede attraverso la riduzione proporzionale degli oggetti, ottenuta senza l’uso di una gabbia geometrica che inquadri le forme ; l’altro utilizza invece l’illusione ottica. Non si tratta di semplice « flessibilità nell’approccio pratico alle tecniche della prospettiva », come si è affermato, ma di scelte operative che offrono una soluzione adeguata e coerente alle diverse esigenze figurative, non previste nel trattato di Alberti De Pictura (1436).
Per finire, va evidenziato che il filo conduttore dell’opera di Piero della Francesca consisteva nel collegare lo studio teorico della matematica all’attività pittorica. La sua figura non può essere pienamente colta se non si comprendono i rapporti tra le riflessioni sulla prospettiva e i suoi dipinti. Appare chiaro, anche ad una lettura di solo alcuni dei suoi scritti più importanti, in particolare del testo De prospectiva pingendi15, che per Piero la prospettiva non fosse un codice da applicare rigidamente, ma una possibilità creativa e che raffigurare lo spazio per mezzo di essa equivalesse a conoscerlo, dapprima in forma oggettiva, mediante la regola matematica e poi a comprenderlo in forma soggettiva attraverso le relazioni fra l’individuo e le cose. Compito del pittore era trascrivere questa comprensione in modo che l’osservatore potesse immedesimarsi con naturalezza nella realtà mostrata dalla pittura, senza che vi fossero elementi capaci di sovvertire le aspettative visive, ma piuttosto confermandole con l’evidenza del riscontro matematico. Per Piero, infatti, il mondo naturale era regolato da leggi « divine » e la matematica era la loro metafora.
- Note de bas de page 16 :
-
Si intende col termine prospettiva un insieme di metodologie che consentono di rappresentare su un piano (o un’altra superficie bidimensionale) oggetti dello spazio tridimensionale, in modo che il disegno rappresenti, il più fedelmente possibile l’oggetto reale, creando quindi l’illusione della visione diretta. Per esigenze di schematizzazione geometrica, la prospettiva generalmente considerata in matematica è la cosiddetta prospettiva lineare o geometrica, contrapposta alla prospettiva aerea che tiene conto anche delle norme da seguire relative alle molteplici variazioni di colore, luce e forma derivanti dalla presenza dell’atmosfera. Il principio di base sul quale si fonda quest’ultima è che gli oggetti della stessa forza di tono impallidiscono nell’allontanarsi in funzione della distanza, a causa dell’aumento della quantità di atmosfera interposta fra essi e l’occhio. Si tratta di fenomeni di luce assai complessi che, con la eccezione della teoria delle ombre, si presta con difficoltà ad una trattazione puramente geometrica. La prospettica lineare, considerata come l’insieme delle regole e delle proprietà geometriche che consentono di risolvere il problema della rappresentazione prospettica, creando l’illusione della visione tridimensionale dell’oggetto, risponde, in un certo senso, a una esigenza più artistica che scientifica. Si osservi a questo riguardo che, assegnata la figura obiettiva, la sua immagine prospettica su un dato quadro e da un dato punto di vista risulta univocamente determinata, ma non altrettanto può dirsi invece per il problema inverso. La prospettiva lineare non ci permette infatti di passare senza ambiguità dalla rappresentazione sul quadro alla figura obiettiva ; l’esigenza di costruire metodi di rappresentazione bidimensionali che consentano la ricostruzione dell’oggetto in forma, posizione e grandezza ha dato luogo ad un importante ramo della matematica, noto come Geometria descrittiva.
Va osservato che lo stretto intreccio di interessi artistici e scientifici è caratteristica comune tra gli artisti rinascimentali, uomini poliedrici e culturalmente pervasi dall’idea di universalità del sapere ; in tale unitarietà dell’attività spirituale, la stessa differenziazione tra scienza e arte sfuma in un interesse totalmente finalizzato alla comprensione del mondo e della natura, delle leggi che li regolano e della loro bellezza. In questo contesto vanno interpretate sia la tanto citata affermazione di Leonardo, « non mi legga chi non è matematico » nel suo Trattato della Pittura, sia la definizione che Piero della Francesca pone all’inizio del Libro Terzo del De Prospectiva Pingendi a sostegno della « necessità » della conoscenza della Prospettiva16 nelle arti visive : « la pictura non è se non dimostrazioni de superficie e de corpi degradati o accresciuti nel termine ».
Nel cercare regole, metodi e modelli per cogliere il reale, gli artisti del Quattrocento italiano diventarono artefici di scoperte scientifiche, grazie alla loro capacità di comprendere la realtà senza prescindere dall’aspetto pratico del sapere, tipico dell’artigiano. In questo contesto umanistico, tendente ad armonizzare in un sistema razionale i molteplici aspetti della realtà, l’arte, attraverso il rigore matematico della prospettiva, mira ad attribuire alla rappresentazione spaziale un carattere di universalità, eliminando casualità e contraddizioni. Lo spazio tridimensionale è di conseguenza necessariamente omogeneo, geometricamente organizzato secondo le leggi della proporzione e dell’armonia (in accordo con il rigore del metodo logico-deduttivo inaugurato da Euclide), e la matematica fornisce al nostro intelletto gli strumenti necessari per la comprensione della bellezza del creato.
6. Tassellazioni piane, modelli di spazio e paradossi percettivi
Il legame tra matematica e arti figurative si è intensificato ogni volta che, da Leonardo ai cubisti, si è cercato di rappresentare figure geometriche, in particolare solidi di varia forma. Nel secolo scorso, l’artista M. C. Escher occupa un ruolo di spicco nello sviluppo del dialogo tra arte e matematica. Escher è stato particolarmente attratto dai poliedri regolari (o solidi platonici) perché questi “simboleggiano in maniera impareggiabile l’umana ricerca di armonia e ordine”. Essi hanno per facce uno stesso poligono regolare, con lo stesso numero di facce ad ogni vertice, e il matematico greco Teeteto scoprì che sono solo cinque : tetraedro, ottaedro, icosaedro, cubo e dodecaedro. Cubo e ottaedro sono detti reciproci, perché uno ha tre facce quadrate in ogni vertice, l’altro quattro facce triangolari. Il tetraedro è reciproco di se stesso, perché ha tre facce triangolari in ogni vertice. L’intersezione di due tetraedri uguali si chiama stella ottangula e ha interessanti proprietà : guardando al suo interno, essa è costituita da un ottaedro sulle cui facce sono state poste piramidi triangolari ; guardando al suo esterno, i vertici della stella sono i vertici di un cubo, le cui facce hanno per diagonali i lati della stella. Questo straordinario poliedro è stato raffigurato da Escher in varie opere, e appare in particolare nell’angolo nord-est di Stelle, disegnato nello stile di Leonardo. Il processo di stellazione (aggiunta di piramidi sulle facce) si può applicare anche al dodecaedro, ottenendo un poliedro di “perfettamente ordinata bellezza” (detto piccolo dodecaedro stellato), che si può vedere come l’intersezione di dodici facce a stella regolare. In Stelle il poliedro principale è l’intersezione di tre ottaedri, disegnati nello stile di Leonardo, e le “stelle” sono in realtà una fantasmagoria di poliedri più o meno regolari.
- Note de bas de page 17 :
-
Formalmente, dato uno spazio X su cui sia definita una distanza d, una funzione ƒ : X → X è una isometria se e solo se ∀ x, y ∈ X si ha che d(x, y) = d(ƒ(x), ƒ(y)). L’insieme delle isometrie che agiscono su un piano euclideo è un gruppo non commutativo. Esso contiene trasformazioni molto intuitive e utilizzate, ad esempio, nella teoria delle tassellazioni del piano. Le traslazioni formano un gruppo commutativo. Le rotazioni, invece, non formano un tale gruppo, perché la composizione di due rotazioni è una rotazione o una traslazione. Inoltre, la composizione di una riflessione e di una rotazione, o di una rotazione e una riflessione è equivalente ad una riflessione. Si osservi che la composizione di una rotazione e di una riflessione non è commutativa. In formule : Rot(θ) Ref(∅) = Ref(∅ + θ/2), Ref(∅) Rot(θ) = Ref(∅ – θ/2). Le isometrie possono essere classificate in isometrie invertenti (o inverse) e isometrie non invertenti (o dirette) ; le prime comprendono le simmetrie assiali e le antitraslazioni, mentre le seconde sono le rotazioni e le traslazioni. Per capire questa distinzione, si consideri un poligono G con n lati i cui vertici siano numerati da 1 a n in senso orario, la sua immagine tramite una isometria invertente avrà i vertici numerati in senso antiorario ; se invece l’isometria è non invertente, l’ordine dei vertici non cambia. È facile osservare che la composizione di un numero qualsiasi di isometrie non invertenti è un’isometria non invertente; in altre parole, le isometrie non invertenti formano un gruppo con l’operazione di composizione. Le isometrie invertenti invece non formano un gruppo ; infatti la composizione di un qualsiasi numero pari di isometrie invertenti dà un’isometria non invertente. Inoltre è ovvio che la composizione di una qualunque isometria invertente con una qualunque isometria non invertente dà un’isometria invertente.
Un uso particolarmente interessante dei poliedri regolari riguarda la possibilità di riempirne l’intero spazio (la cosiddetta tassellazione dello spazio). L’unico dei cinque solidi platonici che riempia da solo lo spazio è il cubo, ma tetraedri e ottaedri alternati (i primi in quantità doppia dei secondi) raggiungono lo stesso scopo. Escher ha rappresentato entrambe queste tassellazioni dello spazio. L’altro problema da lui affrontato riguarda la tassellazione del piano : esso consiste nel ricoprire l’intero piano mediante tasselli, come in un gigantesco puzzle (il problema fu studiato dal punto di vista matematico per la prima volta da Keplero nell’Harmonice mundi, 1619). La grande varietà di possibili tassellazioni può essere circoscritta imponendo opportune limitazioni, di cui le più ovvie sono le seguenti : (i) una tassellazione viene detta monoedrica se usa un solo tipo di tassello, e biedrica se ne usa due ; (ii) una tassellazione viene detta isoedrica se tutti i tasselli hanno la stessa relazione con il resto della tassellazione : in particolare, non solo sono tutti uguali, ma svolgono anche tutti lo stesso ruolo. In termini più matematici, una tassellazione è isoedrica se, dati due tasselli di qualunque tipo, esiste una isometria17 che sposta localmente uno dei due tasselli nell’altro, ma lascia globalmente invariata la tassellazione. (iii) Una tassellazione viene detta monomorfa se è l’unico modo possibile di combinare i tasselli per ricoprire il piano. Ad esempio, gli unici poligoni regolari che riempiano da soli il piano sono il triangolo, il quadrato e l’esagono : la tassellazione mediante esagoni è monomorfa, ma non è così per le tassellazioni realizzate con triangoli o quadrati. Il solo esempio tra le opere di Escher di tassellazione monoedrica ma non isoedrica è Fantasmi : il tassello è unico, ma è usato in maniere diverse (alcuni fantasmi sono raggruppati, altri sono isolati). L’esempio è interessante perché non isoedrico in modo essenziale : ogni tassellazione del piano che usi quel tipo di tassello deve essere non isoedrica (questo deriva dal fatto, non ovvio, che la tassellazione della figura è monomorfa).
Nel passato, molte culture come quella araba o anche nell’arte precolombiana o in quella africana, hanno sviluppato un grande interesse per le figure piane con motivi ripartiti regolarmente in modo tale da ricoprire l’intero piano. Questi motivi ammettono un infinito numero di variazioni, ma esiste solamente un numero finito di modi di riprodurli, esattamente 17. Escher non è certo dunque stato il primo artista ad usare tassellazioni del piano : l’esempio delle decorazioni moresche dell’Alhambra di Granada è ben noto, e fu da lui stesso studiato in maniera approfondita. A causa della proibizione della tradizione islamica (ma non esplicita nel Corano) di rappresentare esseri viventi, i Mori non poterono però usare altro che motivi geometrici astratti, mentre Escher trovò più significative rappresentazioni di figure animate, specialmente pesci e uccelli. Sia i Mori che Escher furono interessati ad una esplorazione sistematica della tassellazione isoedrica, ed usarono quasi tutte le 17 possibili isometrie descritte dal cristallografo russo E. S. Fedorov nel 1891 (più precisamente : 11 i Mori, e 16 Escher). Mentre i Mori dovettero ovviamente scoprire da soli le varie possibilità, Escher conobbe fin dal 1937 un famoso articolo del matematico G. Pólya apparso nel 1924, in cui le 17 possibilità erano state riscoperte e illustrate, e le ricopiò accuratamente. Per esempio, l’opera Cavalieri (una Xilografia realizzata da Escher nel 1946), insieme ai Cigni (1956), è una stampa in cui ricorre esplicitamente la riflessione ; i cavalieri chiari sono l’immagine riflessa di quelli scuri, e si può passare esattamente dall’uno all’altro applicando una glissoriflessione. L’asse di questa trasformazione è ovviamente verticale ed è posizionato o tra le schiene o tra i polsi dei cavalieri ; qui viene comunque dimostrato che i cavalieri chiari e quelli scuri insieme riempiono un’intera superficie. L’originalità matematica di Escher fu ancora più evidente nell’uso delle tassellazioni cromatiche, in cui ogni isometria che lascia invariata la tassellazione permuta i colori in modo non ambiguo. In particolare, Escher ritrovò indipendentemente 14 delle 46 possibili isometrie bicromatiche classificate da J. H. Woods nel 1936, in un lavoro che però rimase ignoto fino agli anni 50, quando i suoi risultati furono riscoperti da A. V. Shubnikov, che in seguito fu entusiasmato dai disegni di Escher.
Il problema della tassellazione si può estendere dal piano euclideo a superfici più complicate. Gli esempi più semplici di tali superfici sono la sfera e il cilindro. La sfera è limitata nello spazio, e può dunque essere internamente tassellata con un numero finito di tasselli. Questo fatto è, secondo Escher, “un meraviglioso simbolo dell’infinito in forma chiusa”, ed egli l’ha illustrato intagliando varie sfere di legno (in particolare la Sfera con angeli e diavoli, 1921). Si noti che il procedimento dell’intagliatura fu usato più tardi da L. Fontana per creare la serie Concetti spaziali, Nature (1959-1960), raffiguranti delle grandi sfere bucate e intagliate in terracotta e in bronzo, che fornivano la rappresentazione della profondità dello spazio e di una possibile articolazione tra nuove dimensioni spaziali e dinamiche temporali. Il cilindro si ottiene incollando fra loro gli estremi di una striscia (infinita in una direzione). Ogni tassellazione del cilindro ne genera una del piano, perché basta ripetere all’infinito la striscia che genera il cilindro. Ma non tutte le 17 tassellazioni isoedriche del piano generano tassellazioni isoedriche del cilindro, perché alcune isometrie si possono perdere. Escher ha illustrato la tassellazione del cilindro piastrellando varie colonne. La striscia di Möbius si ottiene incollando fra loro gli estremi di una striscia (infinita in una direzione), dopo averle fatto compiere un mezzo giro (o, più in generale, un numero dispari di mezzi giri). Essa gode di due interessanti proprietà : ha una sola faccia, invece di due come le solite superfici ; e se la si taglia lungo la linea centrale della striscia non la si separa in due, come per il cilindro, bensì se ne raddoppia la lunghezza (ottenendo una striscia che non è più di Möbius, e che ha due facce). Queste proprietà sono così strane che hanno distratto Escher dal problema della tassellazione, facendogli produrre invece le due efficaci Striscie di Möbius, la prima con un solo giro, la seconda con tre.
- Note de bas de page 18 :
-
Questo lavoro è stato analizzato in dettaglio dal punto di vista matematico da H.S.M. Donald Coxeter. Esso costituisce un ulteriore adattamento della tassellazione del piano euclideo con angeli e diavoli. In quest’opera, però, le ali si incontrano a 4 a 4, e i piedi a 3 a 3. Si può anche notare che tutti gli angeli, così come tutti i diavoli, hanno le stesse dimensioni iperboliche, nonostante l’apparente diminuzione euclidea, dovuta al fatto che le distanze si misurano diversamente nei due casi.
Le tassellazioni iperboliche sono soltanto l’ultimo stadio di una serie di sperimentazioni che Escher effettuò con tassellazioni le cui figure rimpiccioliscono quando si avvicinano a un limite, e che si possono classificare in tre tipi : (i) usando come limite un punto, la tassellazione richiede ancora l’intero piano : infatti le figure si ingrandiscono senza limite a mano a mano che si allontanano dal punto ; (ii) usando come limite una retta, la tassellazione richiede ancora (o solo più) metà del piano. Escher ritenne che il guadagno non fosse molto, e non seppe mai che in tal modo avrebbe invece potuto tassellare secondo il modello di Poincaré ; (iii) usando come limite una circonferenza, come nel Limite del cerchio IV (1960)18, la tassellazione richiede solo più di una zona limitata, pur rimanendo infinita. Questa era proprio la soluzione che Escher aveva invano cercato, senza riuscire a trovarla da solo.
Questa rappresentazione dell’infinito anticipa di qualche decennio la formulazione matematica del concetto di “frattale” ad opera di Benoît Mandelbrot. I frattali sono la descrizione visiva di particolari equazioni matematiche e si presentano come figure autosomiglianti : ingrandendone una parte ci si ritrova alla struttura di partenza, in un processo che può estendersi all’infinito.
Ricordiamo che nel modello di Poincaré valgono le seguenti proprietà : (a) il piano è la regione delimitata da una circonferenza, con l’esclusione della stessa ; (b) il punto è un qualsiasi punto interno alla circonferenza ; di conseguenza, i punti appartenenti al bordo della circonferenza non sono inclusi nel modello ; (c) la retta è ogni diametro della circonferenza e ogni arco di circonferenza ortogonale e interno a questa figura. Si dimostra inoltre che per due punti del piano di Poincaré passa una e una sola retta, e per un punto qualsiasi interno alla circonferenza passano una infinità di rette (cioè archi di cerchio ortogonali alla circonferenza). Un altro modello simile, per il quale valgono le stesse regole e definizioni del precedente, è il semipiano di Poincaré ; in esso il centro della circonferenza è all’infinito e la circonferenza diventa una retta. I diametri diventano una retta perpendicolare alla retta, e gli archi ortonormali, circonferenze aventi il centro sulla retta.
- Note de bas de page 19 :
-
Secondo Rubin, l’organizzarsi della situazione in un insieme figura-sfondo obbedisce a determinate condizioni in base alle quali è possibile prevedere quale zona del campo percettivo acquisterà il ruolo di figura rispetto ad altre zone. Tra le più importanti di tali condizioni ci sono la grandezza delle parti (si percepisce come figura l’area più piccola), i loro rapporti topologici e la tipologia dei loro bordi.
L’interesse di Escher per le tassellazioni non era fine a se stesso, ma ad una loro trasfigurazione artistica. Frammenti di tassellazioni appaiono così in una sessantina di suoi lavori, in cui egli sfruttò a fondo il fatto che in una tassellazione biedrica ciascuno dei due tipi di tasselli svolge due ruoli complementari, di figura e sfondo, secondo un principio basato sul cosiddetto vaso di Rubin (in cui due profili di facce possono essere visti come il contorno di un vaso). Poiché non è però possibile percepire una figura in assenza di sfondo, il risultato è un’alternanza instabile di due figure, ciascuna delle quali viene percepita per un breve periodo sullo sfondo dell’altra. In altre parole, “i profili di Rubin” consentono due soluzioni non percepibili simultaneamente (profili umani o vaso). Alcuni percepiscono per prima la figura antropomorfa, cioè i profili umani, mentre altri, invece, percepiscono per primo il vaso19. Impiegando variazioni dinamiche nelle tassellazioni biedriche secondo principi e tecniche della psicologia della Gestalt, di cui era interessato conoscitore, Escher riuscì ad illustrare convincentemente il passaggio dal bidimensionale al tridimensionale e la morfogenesi, facendo evolvere indipendentemente e gradualmente i due tipi di tasselli in figure indipendenti e spaziali. Simmetricamente, le metamorfosi di Escher evidenziano la sintesi dialettica, fra positivo e negativo, che le tassellazioni biedriche contengono.
6.1. La relazione figura/sfondo e le variazioni del contenuto percettivo
Rubin ha mostrato che l’articolazione « figura-sfondo » obbedisce a determinate condizioni, conoscendo le quali è possibile prevedere quale zona del campo assumerà con maggiore probabilità ruolo di « figura » rispetto alle altre zone. Le più importanti di tali condizioni sono la grandezza relativa delle parti, i loro rapporti topologici e i tipi dei loro bordi. A parità di condizioni, tenderà cioè ad emergere come figura la zona più piccola e così sarà favorita nel ruolo di figura una zona inclusa e delimitata da altre aree, le quali assumeranno piuttosto carattere di sfondo. Un’altra condizione che influisce sulla ripartizione figura-sfondo è la convessità o la concavità dei bordi : in molte figure elementari viene infatti percepita come « figura » preferibilmente la zona verso la quale il bordo curvilineo od angolare volge la propria parte « interna » : a parità delle altre condizioni, tende cioè a diventare figura l’area con bordi convessi piuttosto che quella con bordi concavi. In generale, le figure a bordi convessi tendono a prevalere sulle zone delimitate da bordi concavi, i quali appaiono più facilmente come sfondo inarticolato (cioè privi di forma). Una certa influenza ha l’orientamento spaziale : tendono cioè ad essere « figura » le zone del corpo i cui assi coincidono con le direzioni principali dello spazio, la verticale e l’orizzontale. Naturalmente, quando nessuna delle condizioni menzionate privilegia una parte del campo sulle altre, si ha una situazione di ambiguità, nella quale domina l’instabilità e la continua reversibilità del rapporto figura-sfondo. In tal caso, esercita un certo ruolo anche l’impostazione soggettiva dell’osservatore, che mediante la direzione dell’attenzione può influire sulla ripartizione figura-sfondo risultante.
La percezione di certe figure “paradossali” (o certi oggetti “impossibili”) è legata alla questione della relazione figura-sfondo. Dal punto di vista percettivo esistono notevoli differenze funzionali tra la regione del campo che assume carattere di figura e quella che svolge il ruolo di sfondo. La figura ha carattere oggettuale, è una « cosa », mentre per lo sfondo tale carattere è molto meno pronunciato, fino a mancare quasi del tutto quando lo sfondo è vissuto come spazio vuoto. La figura ha un aspetto più solido, le sue superfici hanno un colore più compatto, anche se per caso riflettono fisicamente lo stesso tipo e la stessa quantità di luce dello sfondo. La figura possiede un maggiore risalto, attira lo sguardo, è ciò di cui normalmente ci occupiamo, a cui facciamo attenzione molto più che allo sfondo. Solo la figura ha un contorno, i bordi delimitano la figura ma non servono a delimitare lo sfondo che invece passa dietro alla figura. Anche per quanto riguarda la localizzazione spaziale vi è dunque una distinzione : in genere la figura sta davanti o sopra lo sfondo.
Alcune delle opere più famose di Escher sono perfette illustrazioni della validità logica dei cosiddetti « oggetti impossibili », oltre che di alcuni ben noti paradossi percettivi, basati sul contrasto tra percezione e interpretazione dei dati sensoriali, e sul condizionamento fisiologico e culturale che spinge a considerare figure bidimensionali come rappresentazioni di oggetti tridimensionali. La litografia Belvedere è ispirata al cubo di Necker, che si ottiene disegnando un cubo in prospettiva con tutti i lati in evidenza : così facendo si crea un’ambiguità su quale delle facce sia davanti e quale dietro, e due possibili cubi si alternano nella percezione. Il cubo di Necker è disegnato nel progetto che sta ai piedi del personaggio seduto sulla panca (con i due punti problematici evidenziati), ed egli tiene in mano un modello di cubo impossibile, in cui l’ambiguità viene risolta fondendo le due possibilità, e creando così un cubo localmente corretto (nella parte alta e in quella bassa), ma globalmente impossibile. L’edificio della figura realizza poi il cubo impossibile, congiungendo paradossalmente la parte alta e quella bassa, che sono separatamente consistenti. Altri casi di ambiguità percettive particolarmente significative risaltano nelle opere Convesso e concavo, nella scala di Schröder, e in Relatività, che combina la scala di Schröder con il triangolo impossibile. Un uso spettacolare del triangolo impossibile si ha in Cascata, dove esso appare tre volte consecutive nella rappresentazione di un canale che sembra localmente in piano, ma globalmente in salita. Escher crea così l’impressione doppiamente paradossale, da un punto di vista fisico, di un moto perpetuo generato dall’acqua che scorre all’insù. Si noti come l’intera figura sia in realtà la sovrapposizione di due figure separatamente consistenti : due torri (una a tre piani e l’altra a due), ed un canale orizzontale (con i lati due a due perpendicolari). In Salire e scendere si rappresenta infine la scala di Penrose (padre), in cui un moto perpetuo è generato in modo opposto a quello di Cascata : non mediante un percorso in salita che dovrebbe essere in piano, ma da un percorso in piano che dovrebbe essere in salita. Che la scala sia in piano lo si intuisce tenendo l’immagine non perpendicolarmente al campo visivo (come normalmente la si osserva), ma (quasi) parallelamente ad esso. Gli scalini sono in realtà posti uno sull’altro come tegole su un tetto piano, o libri su un tavolo, in modo da formare un quadrilatero : l’illusione deriva dal disegnare come verticali i prolungamenti delle altezze degli scalini, che sono in realtà linee oblique. Poiché però tali prolungamenti vanno in direzioni opposte su lati opposti del quadrilatero, l’edificio si può disegnare solo a metà, ed esso non potrebbe stare in piedi. Paradosso a parte, Escher vide qui una metafora dell’assurdità della vita, non solo del “come è duro calle lo scendere e’l salir per l’altrui scale” (Paradiso, XVII, 59-60), ma anche di quanto tale affanno sia inutile, e non porti in realtà da nessuna parte.
In conclusione, possiamo dividere i sei paradossi percettivi usati da Escher in due classi. Tre di essi (il cubo di Necker, i cubi reversibili e la scala di Schröder) sono semplicemente figure ambigue, che rappresentano più di un oggetto allo stesso tempo, su cui la percezione è incerta e non riesce a decidere. I rimanenti tre (cubo impossibile, triangolo impossibile e scala di Penrose) sono invece figure assurde, che rappresentano un solo oggetto ben definito. L’assurdità delle figure del secondo gruppo è però di un tipo molto particolare : essa risiede soltanto nella loro interpretazione, e non nel fatto che esse siano rappresentazioni di percezioni impossibili. Si è infatti mostrato, per esempio, come una serie di sbarre perpendicolari due a due (ovviamente formanti non un triangolo chiuso, ma una figura aperta) possa sembrare un triangolo impossibile, se osservato da un particolare punto di vista. Analogamente, un modello di cubo con due lati discontinui può sembrare un cubo impossibile, se osservato da un particolare punto di vista (perché le discontinuità permettono di vedere lati che stanno in realtà sul retro).