Sémiotique des graphiques / Graphiques de sémiotique
- Note de bas de page 1 :
-
Sémir Badir, Textes et Graphiques. Contribution à une épistémologie sémiotique, Thèse d’agrégation, Université de Liège, 2007.
- Note de bas de page 2 :
-
Id., « À quoi servent les graphiques », Visible, n° 1, 2005, pp. 173-194.
Dans cette étude, on regardera un certain nombre de graphiques —schémas, tableaux, diagrammes — employés dans les travaux des sémioticiens. La présente étude fait suite à deux autres : l’une consacrée à l’étude des schémas présents dans les premières pages du Résumé d’une théorie du langage de Hjelmslev1, l’autre consacrée à la mise en évidence d’invariantes pour la sémiotique des graphiques, sur le plan de l’expression comme sur celui du contenu2. C’est dire qu’on ne regardera pas les graphiques de ce corpus avec des yeux absolument neufs mais qu’on sera prévenu de certains enjeux et problèmes théoriques qui peuvent être posés lorsqu’on examine des graphiques, et des graphiques de sémiotique en particulier.
- Note de bas de page 3 :
-
Par exemple, dans la définition qu’en donne Jacques Bertin, Sémiologie graphique, Paris, Gauthier-Villars, La Haye, Mouton, 1967, p. 8, ou dans le titre même de l’ouvrage de Ann Harleman Stewart, Graphic Representation of Models in Linguistics, Bloomington, Indiana U.P., 1976.
L’un de ces problèmes mérite d’être traité de façon préliminaire, à titre de réquisit méthodologique. Il concerne le rapport du graphique à son objet ou, uniment, le rapport du graphique au texte dans lequel celui-ci est inséré. Le terme de représentation, si souvent accolé au terme de graphique3, lequel devient alors un adjectif, concentre les difficultés inhérentes à ce double rapport. Parler des graphiques en termes de « représentations graphiques » inscrit leur étude dans une sémiotique référentielle triviale (on pose sans conditions l’existence des objets soi-disant représentés) et statue d’avance sur les relations intersémiotiques entre texte écrit, graphique et objet. Une telle conception de la fonction sémiotique des graphiques est dommageable à plus d’un titre : elle ne permet pas de rendre compte adéquatement de leur contenu, alors réduit à une fonction vague et invariable, ni de faire état du statut des parties qui les composent, car ce n’est pas nécessairement en n’importe quelle de leurs composantes, et de n’importe quelle manière, que les graphiques sont supposés représenter leur objet.
- Note de bas de page 4 :
-
Algirdas Julien Greimas, Du Sens II, Seuil, 1983, p. 192.
Prenons, à titre d’illustration pour la discussion de ce préalable théorique, un carré sémiotique extrait d’un article de Greimas initialement publié en 19794.
- Note de bas de page 5 :
-
Les titres donnés aux figures sont de mon cru, sauf indication par des guillemets.
Fig. 1 - Carré sémiotique des modalités épistémiques
(in Greimas, Du Sens II)5
Ce graphique entend, selon l’auteur, dégager la structure formelle de la signification d’un article de Georges Dumézil concernant les sciences humaines. Il manifeste une analyse de ce texte et peut, de ce fait, être situé à un niveau métasémiotique vis-à-vis du niveau sémiotique du texte-objet, désignant les formes sémantiques de ce dernier par des termes métasémiotiques et faisant état des relations entre ces formes au moyen de deux doubles flèches entrecroisées. De quelque manière qu’on aborde le rapport que ce graphique entretient avec son texte-objet, on ne saurait se satisfaire d’un rapport de représentation : aucune composante contenue dans ce graphique ne représente le texte de Dumézil, mais toutes contribuent à son analyse. Pas davantage on ne saurait admettre que le graphique représente l’analyse du texte de Dumézil : il la manifeste, seulement. Dans l’article de Greimas, il en est du reste l’unique manifestation. Or, quand bien même des paragraphes verbaux énonceraient, dans cet article ou ailleurs, la même analyse, il n’y aurait pas encore lieu de dire que l’une de ces manifestations sémiotiques est postérieure à l’autre et qu’elle re-présente ce qui a été présenté précédemment. Paragraphes et formats graphiques entretiennent un rapport équivalent vis-à-vis du texte-objet, sans qu’on ait à faire valoir la prévalence des uns sur les autres.
Dans la présente étude, on partira donc du postulat théorique consistant à admettre que le langage graphique possède des constantes de contenu qui lui sont propres. Sans ce postulat, le contenu des graphiques demanderait à être étudié en fonction des objets que ceux-ci sont supposés représenter. Tout au contraire, la démarche qui sera la nôtre consiste à ignorer systématiquement les objets dont les graphiques sémiotiques produisent des analyses, pour nous pencher sur ces analyses elles-mêmes, selon leurs différentes composantes et leur variété. Ainsi, dans le graphique pris en guise d’illustration dans la figure 1, on ne cherchera pas à connaître les raisons qui peuvent être alléguées pour que certitude, probabilité, improbabilité et incertitude soient recevables comme termes métasémiotiques pour les formes sémantiques contenues dans le texte de Dumézil, mais bien à déterminer de quelle manière ces termes participent ici à un agencement graphique, et quel type d’analyse est ainsi manifesté. Si on trouvait aux extrémités d’une des flèches doubles, au lieu de certitude et incertitude, mort et non-mort, et aux extrémités de l’autre, au lieu de probabilité et improbabilité, vie et non-vie, le commentaire à produire dans cette étude pourrait être maintenu identique dans les deux cas. Cela revient à dire que certitude et incertitude, d’un côté, mort et non-mort, de l’autre ne constituent pas les composantes à étudier, mais les simples manifestations variables d’une constante métasémiotique valable pour n’importe quel objet dont le graphique présente l’analyse, que cet objet soit un objet empirique (ce cas ne se rencontre pas dans le corpus de graphiques sémiotiques qui a été rassemblé pour cette étude), un texte, comme dans le graphique de la figure 1, ou encore un objet déjà métasémiotique (ce cas est, quant à lui, assez fréquent dans notre corpus), et pourquoi pas alors lui-même graphique.
Toutefois, la visée de la présente étude se situe au-delà de la vérification du postulat théorique dont il vient d’être brièvement question. Le corpus rassemblé présente en effet la particularité remarquable de constituer une série. Il ne s’agira pas dès lors seulement de rechercher les constantes du plan de contenu graphique mais d’observer, dans un premier temps, de quelle manière ces constantes graphiques ont émergé, puis, dans un second temps, de voir leurs manifestations évoluer jusqu’à provoquer l’apparition de nouvelles constantes. On considérera donc ici que, de Hjelmslev à Zilberberg, en passant par Greimas, chaque nouveau graphique aura été l’interprétation des graphiques antérieurs, quel que soit par ailleurs les objets traités par les uns et les autres.
Convenons d’emblée que cette particularité n’est pas ordinaire et ne se rencontrerait pas dans un corpus élargi. Elle soutient toutefois le postulat théorique évoqué plus haut selon lequel une sémiotique propre peut être dégagée de la pratique des graphiques et est capable de générer des énoncés à partir d’énoncés antérieurs appartenant au même système sémiotique. Elle présente en outre un intérêt spécifique pour l’étude du discours sémiotique : cette particularité va de pair avec la capacité de la sémiotique à produire une autocritique. Ce n’est pas une pratique indifférenciée du langage graphique qui permettra la critique des graphiques proposés successivement par les auteurs de notre corpus, mais bien la pratique sémiotique elle-même, comme nous allons le voir, par sa capacité à générer des graphiques de remplacement dont la légitimité n’a pas à dépasser le cadre de sa réflexion théorique. On considérera donc que les graphiques employés en sémiotique produisent un usage sémiotique propre à cette pratique de recherches et d’écriture, ce qui justifie les syntagmes en miroir proposé pour titre à cette étude.
Hjelmslev
- Note de bas de page 6 :
-
Louis Hjelmslev, « Résumé d’une théorie du langage » [extrait] in Nouveaux essais, Paris, P.U.F., coll. Formes sémiotiques, p. 90.
- Note de bas de page 7 :
-
Ibid., p. 109.
- Note de bas de page 8 :
-
Louis Hjelmslev, Résumé of a Theory of Language, Travaux du cercle linguistique de Copenhague XVI, Copenhague, Nordisk Sprog-og Kulturforlag, 1975, p. 60.
Commençons par constater l’existence nombreuse et régulière des graphiques dans l’œuvre de Hjelmslev : on en trouve dans tous ses ouvrages. Dans le Résumé, les graphiques sont d’abord présentés en note (« N 2 : Représentation graphique de Déf 3 », « N 4 : Représentation graphique de Déf 4 et 5 »6, etc.) mais bientôt ils font partie du corps même des définitions et des règles. Ceci se vérifie en particulier en ce qui concerne la description des classes (« Rg 16 »7), pour laquelle il n’existe pas d’autres relais descriptifs, ainsi que celle des fonctions (« Df 138 »8), dans laquelle sont distribués les symboles attachés aux fonctions selon les différentes classes. Aussi est-il raisonnable de penser que les graphiques constituent un moyen d’expression nullement superflu dans la pensée hjelmslevienne.
- Note de bas de page 9 :
-
Ibid., p. 3 [ma trad.].
Rappelons alors en quelques points ce qui peut être rapporté spécifiquement à la compréhension de la production graphique dans le Résumé, tel que le graphique présenté dans la Note 2 a pu en constituer le départ9.
Fig. 2 - L’analyse (Hjelmslev, Résumé to a Theory of Langage)
- Note de bas de page 10 :
-
Sur l’épivisuel, et sur le concept plus général d’épisémiotique, on renverra à S. Badir, « À quoi servent les graphiques », art. cit. ; Id., Textes et Graphiques, op. cit.
-
Le graphique est accompagné de signes indexicaux (ou d’embrayeurs, comme on voudra bien les nommer) qui sont pour partie eux-mêmes graphiques (flèches et parenthèse) et pour partie linguistiques (syntagmes nominaux). Il importe naturellement d’admettre cette distribution mais elle ne dépend que d’une pratique, selon laquelle le graphique est ordinairement accompagné de tels signes, et d’une lecture capable d’en énoncer la critique, car il est évident que rien dans le graphique ne distingue le niveau supérieur des autres sinon cette parenthèse qui, pourtant, n’en fait pas partie, du moins pas au même titre que les autres éléments. Autrement dit, le graphique fait voir des niveaux différents mais pour opérer un regroupement particulier parmi ceux-ci, il est besoin de moyens graphiques additionnels dont la fonction est en outre confirmée par des syntagmes nominaux. En ce sens, la fonction des signes indexicaux est épivisuelle10 : elle « met le doigt » sur la présentation graphique afin d’attirer l’œil non sur l’un ou l’autre de ses objets mais sur une des particularités de son agencement propre (sur un aspect de son « langage », si l’on veut).
-
Le graphique est fait de cases et de segments linéaires. Chacun de ces éléments distinctifs correspond à un concept théorique : les cases, aux objets ; les lignes, aux dépendances. Il est apparu cependant que les segments linéaires peuvent être interprétés soit comme composés de segments discontinus, comme ils apparaissent effectivement dans ce graphique, soit comme formant un segment continûment divisé, ces interprétations renvoyant respectivement soit à des dépendances distinctes quoique homogènes, soit à une seule dépendance uniforme. Le graphique permet de visualiser ici une difficulté théorique, à savoir le glissement du général au particulier concernant le concept de dépendance (selon la version anglaise du Résumé, on passe de « the uniform dependence », dans la Déf 3, à « a dependence », dans la Déf 6). Il s’agit d’une difficulté parce que ce glissement du général au particulier n’est nullement commenté par Hjelmslev.
-
Le graphique établit des divisions binaires. En cela, il détermine les divisions davantage que ne le fait la définition de l’analyse. Le graphique ajoute donc ici une détermination qui n’est pas contenue dans le texte et, de ce fait, il est en lui-même un levier de questionnement et de découverte pour la réflexion théorique. Ce point est différent du précédent : en ce qui concerne la dépendance, le texte du Résumé est ambigu ; en ce qui concerne l’analyse, il se tient seulement en retrait. Dans le point précédent, la critique devait se reporter au texte, même si c’est le graphique qui en faisait ressortir la nécessité ; dans le cas présent, elle peut porter directement sur la présentation graphique.
-
Enfin, le graphique présente une distribution absolument régulière entre les segments et les cases, c’est-à-dire entre les objets et leurs dépendances. Bien que cette régularité devrait elle aussi être interrogée (ce qui nous ramènerait au point précédent), il apparaît que sa visualisation accomplit une synthèse d’une très grande portée pour la compréhension de la théorie du langage. En dépit de l’enchaînement des définitions et de la complexité conceptuelle qui s’ensuit, il devient en effet possible de se rapporter toujours à un seul et même graphique pour la compréhension des concepts hjelmsleviens. Cherchez-vous à visualiser une syntagmatique ? Le graphique de l’analyse doit y pourvoir, étant donné qu’une syntagmatique est un objet soumis à une analyse. Voulez-vous une somme ? Continuez de vous y reporter, puisqu’une somme est également un objet d’analyse. Qui plus est, le graphique contient en puissance l’ensemble des concepts hjelmsleviens, puisque leur enchaînement est établi au travers de leurs définitions à partir de la définition de l’analyse. Dans un seul graphique, vous pouvez donc visualiser le plan de l’expression et le plan du contenu d’une sémiotique, la paradigmatique ou la syntagmatique congruente à chacun de ces plans, les constantes et les variables qui les analysent jusqu’aux invariantes du dernier degré, mais aussi les sémiotiques connotatives et les métasémiotiques dont cette sémiotique constitue l’un ou l’autre plan. Il n’est qu’une seule exception à la synthèse graphique, et cette exception est très éclairante en elle-même : le graphique de l’analyse peut assurément présenter une syntagmatique comme une paradigmatique, mais jamais ensemble ; aucune de ses divisions ne correspond par conséquent à la distribution conceptuelle entre paradigmatique et syntagmatique. À cette exception près, le graphique détient un caractère général par rapport aux concepts hjelmsleviens : il s’applique à chacun d’entre eux, non sans doute avec le même degré d’adéquation, mais tout de même avec la même pertinence. Cela dit naturellement quelque chose sur les concepts eux-mêmes qui n’est pas dit par leurs définitions prises une à une. Précisons que ce pouvoir synthétique est à distinguer du pouvoir graphique énoncé dans le point précédent, lequel était un pouvoir analytique : là, le graphique apporte un élément d’analyse supplémentaire au regard de la définition de l’analyse ; ici, au contraire, il retranche des particularités définitionnelles afin de pouvoir correspondre à n’importe quel concept hjelmslevien (ou à presque n’importe lequel), et même fait-il davantage : il les comprend tous ensemble (paradigmatique et syntagmatique exceptées).
- Note de bas de page 11 :
-
L. Hjelmslev, Prolégomènes à une théorie du langage suivi de La Structure fondamentale du langage (1943), Minuit, coll. Arguments, 2e éd. révisée, 1971, p. 71.
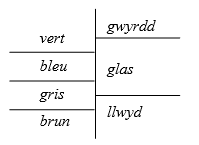
Étant donné que dans la série des graphiques sémiotiques que nous allons étudier la binarité est un élément récurrent, je dois tout de même évoquer deux graphiques, ou plutôt deux sortes de graphiques, qui chez Hjelmslev opposent un démenti au caractère nécessaire de la binarité. Le premier vient des Prolégomènes à une théorie du langage où il connaît deux exemples appliqués au même problème théorique. Hjelmslev l’introduit comme un « tableau schématique faisant voir immédiatement la non-concordance des frontières »11 bien qu’en réalité il s’agisse d’autre chose. Voici le premier d’entre eux :
Fig. 3 - Non-concordance des formes de contenu d’un même paradigme entre deux langues (Hjelmslev, Prolégomènes à une théorie du langage)
- Note de bas de page 12 :
-
Cf. S. Badir, « À quoi servent les graphiques », art. cit.
Contrairement à ce que prétend Hjelmslev, on ne peut considérer sans difficultés que ce graphique est un tableau au sens commun du terme. En effet, les lignes de partage entre formes de contenu au sein d’une même langue (lignes horizontales) ne coïncident pas d’une langue à l’autre (ligne verticale). En outre, les lignes horizontales ne servent pas à classer les objets qu’elles séparent, fonction ordinairement assignée aux tableaux, mais font voir des rapports entre forme et substance différents selon les langues. On reconnaît dans cette fonction un semblant — un semblant, seulement — d’analyse phénoménologique, ainsi que la possibilité théorique en a été observée12 : le graphique invente pour le concept de substance une substance phénoménale, à savoir une étendue circonscrite par les extrémités de la ligne verticale et parcellisée au moyen des lignes horizontales. Par ce semblant d’analyse phénoménologique le graphique permet de présenter de manière visuelle un autre type d’analyse, en l’occurrence une analyse sémiotique.
- Note de bas de page 13 :
-
L. Hjelmslev, Prolégomènes à une théorie du langage, op. cit., p. 72.
- Note de bas de page 14 :
-
« Pur » en ce sens qu’auparavant (L. Hjelmslev, La Catégorie des cas. Étude de grammaire générale, Aarhus, Acta Jutlandica VII, p. 12 ; 56 ; 64) on aura déjà aperçu des tableaux utilisant les mêmes symboles. Dans le cas présent, il ne s’agit plus de tableaux mais bien de schémas à portée générale.
Doit-on soupçonner de la binarité dans ce graphique ? La ligne verticale en indique une mais elle est contingente, comme le montre le second exemple de graphique de ce type13 où deux lignes verticales démarquent les formes de trois langues différentes. Pour le reste, rien n’appelle la binarité dans le graphique reproduit ci-dessus. Il n’en est pas tout à fait de même de l’autre type des graphiques qu’emploie Hjelmslev pour la présentation de formes de contenu. Il s’agit, dans la Catégorie des cas (ainsi que dans le Résumé), des schémas à trois cases, dont les premiers exemples purs14 se trouvent à la page 100 :
Fig. 4 - Cas du locatif et du nominatif selon la direction (Hjelmslev, La Catégorie des cas)
Certes, tous les schémas de la sorte comportent trois cases mais les symboles qui les accompagnent indiquent clairement une polarité binaire (positif / négatif) à quoi est adjoint un état neutre. En outre, dans le Résumé, ces schémas à trois cases cohabitent avec des schémas à deux cases, et des règles sont établies afin qu’une conversion universelle permette aux objets qu’ils présentent (à savoir des corrélations) de passer de trois à deux champs (chaque case graphique ayant pour objet un champ) et vice versa. Les schémas à trois cases restent néanmoins majoritaires et c’est par eux que sont présentés les graphiques des sept types de corrélats (un corrélat est présenté par un schéma à trois cases avec une ou deux diagonales dans une, deux ou trois de ses cases ; les exemples ci-dessus sont donc des schémas de corrélats).
Greimas
- Note de bas de page 15 :
-
A. J. Greimas « Pour une théorie de l’interprétation mythique » (1966), in Id., Du Sens, Seuil, 1970, p. 196.
Chez Greimas comme chez Hjelmslev les textes combinent des paragraphes verbaux avec des formats graphiques et des formulations symboliques. Mais alors que les formulations symboliques peuvent interrompre un paragraphe sans aucun élément verbal introducteur, les graphiques sont présentés en fin de paragraphe et sont fréquemment introduits ou commentés. Commençons par nous intéresser par ces phrases d’introduction et de commentaire. Considérons par exemple l’introduction verbale du graphique suivant, produit dans un article contemporain de Sémantique structurale15 :
Ainsi, à titre d’exemple, le code alimentaire pourrait être présenté, partiellement, sous forme d’un arbre :
Fig. 5 - Code alimentaire chez Lévi-Strauss (Greimas, Du Sens)
Deux éléments de la formule d’introduction sont à pointer :
- Note de bas de page 16 :
-
L’idée d’arbre n’est en fait que suggérée « verbalement » dans l’Isagoge « mais la tradition médiévale a visualisé le projet » (Umberto Eco, Sémiotique et philosophie du langage (1984), P.U.F., coll. Formes sémiotiques, 1998, p. 98). Cette « visualisation » mériterait une étude approfondie qui reste à faire.
-
le verbe présenter. Le rapport entre le graphique et son objet n’est plus de représentation, comme c’était le cas chez Hjelmslev (à tout le moins dans le Résumé), mais bien un rapport de présentation. Ce n’est pas la première fois, dans l’article, que Greimas aborde la corrélation du cru et du cuit, d’après une lecture de Lévi-Strauss, et par ailleurs le code bénéficie d’une définition dans le paragraphe qui précède le graphique ; celui-ci n’en demeure pas moins la seule présentation d’un « code alimentaire ».
-
le nom attribué à ce graphique : arbre. L’arbre est un graphique dûment répertorié depuis la philosophie de l’Antiquité. Porphyre suggère une interprétation sous cette forme de la doctrine contenue dans les Catégories d’Aristote relative à la définition de l’espèce par le genre et la différence spécifique16. En accolant, au niveau inférieur, des termes en caractères romains mis entre parenthèses avec les termes italiques conformes aux termes employés aux niveaux supérieurs, Greimas semble bien reconduire ici non seulement un mode de présentation graphique mais également la théorie sémantique qu’elle soutient dès l’origine : ainsi, le jaguar (espèce) est du frais (genre) animal (différence spécifique).
- Note de bas de page 17 :
-
A. J. Greimas, Sémantique structurale. Recherche de méthode, Larousse, coll. Langue et langage, 1966, p. 33.
Par contre, dans Sémantique structurale, un graphique à peu près semblable à celui qui est reproduit ci-dessus est assorti du commentaire suivant : « Ce schéma représente […] ce qu’on pourrait appeler le système sémique de la spatialité »17.
- Note de bas de page 18 :
-
Je suis en accord sur ce point avec Umberto Eco (Sémiotique et philosophie du langage, op. cit., pp. 86-87), quoique celui-ci l’entende comme une critique à l’endroit de la figure hjelmslevienne.
On le voit, Greimas ne se tient pas à une seule terminologie, ni pour la fonction graphique (présenter ou représenter), ni pour le type de graphique (arbre, schéma et, en guise de formule d’introduction pour le même graphique, tableau), et pas davantage pour l’objet (code ou système sémique). Si l’on ne peut guère tirer de conclusion de ce flou terminologique, en revanche il éclaire a contrario certains des graphiques hjelmsleviens. Le graphique de l’analyse reproduit plus haut (Fig. 2) n’est pas, quant à lui, un arbre selon la tradition instituée par Porphyre18. Il y a deux raisons à cela : primo, nous avons vu qu’à chaque élément graphique correspond un objet, en ce compris les segments linéaires qui « représentent » la dépendance (ou des dépendances), alors que dans un arbre de Porphyre les segments linéaires ne sont pas conceptualisés ; secundo, il ne saurait y avoir, au niveau inférieur du schéma hjelmslevien, deux termes adjoints à une même case.
Toutefois, en dépit de ces différences, il est manifeste que les schémas de Greimas cherchent à imiter ceux de Hjelmslev, tant par leur expression que par leurs objets. Chez les deux auteurs, en effet, les graphiques sont à même de présenter, par une hiérarchie à embranchements binaires successifs, une analyse des formes d’un contenu linguistique. C’est là leur rôle déclaré chez Greimas ; chez Hjelmslev, le graphique du concept d’analyse (Fig. 2) doit pouvoir répondre d’une analyse particulière (même si nous avons reconnu qu’à d’autres endroits de son œuvre ces analyses particulières apparaissent sous des formes graphiques différentes). Or, si l’on a pu constater que, dans le cas de l’analyse particulière des formes de contenu, la binarité n’était pas nécessairement présente dans les analyses hjelmsleviennes, chez Greimas elle va au contraire s’accentuer de transposition en transposition.
Penchons-nous ainsi à présent sur les graphiques greimassiens proprement dits. Et laissons-nous le temps de les découvrir sans préjuger ce qu’il y a à en dire. Certes, la binarité va servir de fil rouge mais il ne me paraît pas judicieux d’en limiter la problématique, chez Greimas, à la seule relation qui lie ses travaux à la pensée de Hjelmslev. Il est évident au contraire que Greimas subit également l’influence d’autres théoriciens, et on ne compte évidemment pas pour rien la poursuite d’intérêts propres à l’auteur. Apprêtons-nous dès lors à un parcours sinueux parmi cette œuvre.
- Note de bas de page 19 :
-
A. J. Greimas, Du Sens, op. cit., p. 212.
- Note de bas de page 20 :
-
Par format, j’entends une forme prégnante, un agencement actualisable dans une production sémiotique englobante ; le paragraphe d’écriture verbale, l’arbre, le tableau, la formule de notation symbolique sont des formats.
- Note de bas de page 21 :
-
La formule est un des formats de base des langages symboliques ; il se combine généralement avec d’autres formats (en particulier, avec des paragraphes) et peut comprendre des formants autres que les symboles (notamment des éléments verbaux).
- Note de bas de page 22 :
-
L’emploi d’un symbole n’est au demeurant que l’élément le plus évident de cette formule ; il faudrait, pour être complet, souligner également l’usage des italiques et la mise en place de blancs équidistants entre les termes.
Le graphique qui a été reproduit plus haut (Fig. 5) est intégré dans un article qui en compte neuf autres : sept tableaux, un graphique hybride à mi-chemin entre le tableau et le diagramme19 et un autre graphique hybride à mi-chemin entre le tableau et le schéma, qui sera reproduit plus bas (Fig. 12), ce dernier graphique contenant, comme on va pouvoir le constater, l’ébauche du carré sémiotique. Chacun de ces graphiques correspond à un format20 — à plusieurs, dans le cas des hybrides — attesté de graphique mais comporte également des éléments qui ne relèvent pas seulement de la sémiotique graphique (la très grande majorité des graphiques réalisés étant, comme attendu, polysémiotiques). Les éléments non graphiques sont de deux sortes : des éléments verbaux et des symboles, lesquels entrent également dans la composition d’autres formats, qui peuvent être ou bien imbriqués dans les graphiques, ou bien accolés avec eux dans l’unité de réalisation qu’est l’article en question. Ces formats autres que graphiques sont les suivants : des paragraphes, des listes (éléments verbaux numérotés), des scripts (éléments verbaux numérotés et hiérarchisés), enfin des formules21. Je prends la peine de décrire ce corpus parce que la transposition que nous avons à considérer fait intervenir deux sortes de formats : le graphique et la formule. Le format formulaire sert d’ailleurs chez Greimas d’interface entre le graphique et le paragraphe puisqu’on trouve des formules aussi bien insérées à l’intérieur d’un paragraphe (par le moyen des parenthèses) que contenues dans les cases d’un tableau. Il est du reste à noter que l’arbre (Fig. 5) présente lui-même un format hybride : au niveau supérieur, cru est mis en rapport avec cuit, non par un moyen graphique, mais bien par un moyen formulaire (utilisation du symbole vs)22.
- Note de bas de page 23 :
-
Le symbole employé par Greimas, inconnu de la police de caractères employées pour cet ouvrage, juxtapose horizontalement un tilde avec une seule des barres droites du symbole de l’égalité. J’ose espérer qu’on acceptera que je lui substitue sans falsification le symbole ≅.
- Note de bas de page 24 :
-
A. J. Greimas, Sémantique structurale, op. cit., p. 196 et 198.
Deux symboles servent abondamment dans les formules comme dans les graphiques ; il s’agit d’un symbole d’opposition — vs (versus) — et d’un symbole de corrélation — ≅ 23. Il est intéressant d’observer qu’ils sont placés dans des situations semblables et que Greimas ne cherche ni à en différencier les usages ni à expliquer les rapprochements qu’ils induisent. Ceci apparaît très nettement dans Sémantique structurale où, à deux pages d’intervalle, on trouve deux formules ne se différenciant que par l’emploi de l’un ou l’autre symbole (les autres différences, dans le choix du symbole alphabétique et dans l’ordre syntagmatique des rapports, pouvant être tenues pour non significatives)24.
Fig. 6 & 7 - Deux structurations narratives (Greimas, Sémantique structurale)
- Note de bas de page 25 :
-
Ibid., p.196.
Certes, les symboles alphabétiques renvoient à des éléments verbaux qui imposent de considérer leurs objets respectifs comme distincts. La première formule présente un système sémique « où chacun des termes manifeste […] une articulation catégorique »25 ; dans la seconde, les symboles alphabétiques renvoient à des fonctions narratives (différenciées elles aussi selon des articulations catégoriques). Il n’empêche que, hors recours aux commentaires verbaux, le rapprochement entre les formules est éloquent. Dans les deux cas, elles sont entièrement dévolues à exprimer la binarité : parce qu’elles établissent soit une corrélation proportionnelle soit une opposition, et parce que les éléments qu’elles mettent ainsi en rapport sont déjà en eux-mêmes le résultat d’une double dichotomisation.
- Note de bas de page 26 :
-
Exemple : « pourri ≅ eau mortelle » (A. J. Greimas, Du Sens, op. cit., p. 219).
- Note de bas de page 27 :
-
Exemple pair :
« contenu topique vs contenu corrélé
contenu posé vs contenu inversé » (Ibid., p. 198).
L’alignement du symbole souligne la juxtaposition des deux formules. - Note de bas de page 28 :
-
Ibid., p. 214.
Pour revenir au corpus de l’article examiné, on y constate que les formules où apparaissent des signes de corrélation n’établissent pas toujours de proportion26 et, en retour, que les formules où apparaissent des signes d’opposition sont quant à elles souvent présentées par groupes (mais pas toujours par paires)27. Or il n’est sans doute pas indifférent qu’une corrélation est définie par Hjelmslev comme une fonction paradigmatique, dont l’opposition (en terme hjelmslevien : la complémentarité) et la catégorisation (la spécification) sont des espèces particulières. La majorité des tableaux présentés par Greimas associent ces deux types de fonctions paradigmatiques. Considérons pour sa simplicité le tableau suivant28 :
Alimentation
|
animale (en haut) |
végétale (en bas) |
||
|
échec |
réussite |
échec |
réussite |
Fig. 8 - Structure d’un récit Bororo (Greimas, Du Sens)
De ce tableau, on déduit aisément des rapports d’opposition (entre animale et végétale, d’une part, entre échec et réussite, d’autre part), mais aussi des rapports de catégorisation (entre les termes de la première opposition et ceux de la deuxième). Si le tableau n’avait pas pour objet un parcours narratif relatif à une quête alimentaire, il pourrait aussi bien être présenté selon une hiérarchie qui inverse le rapport entre les deux oppositions. Soit :
|
échec |
réussite |
||
|
animale |
végétale |
animale |
végétale |
Fig. 9 - Permutation de la hiérarchie contenue dans Fig. 8
C’est dire que les corrélations ne sont pas nécessairement orientées mais qu’elles sont susceptibles d’établir, à un certain niveau de généralité descriptive, une corrélation proportionnelle entre deux oppositions, quelle que soit l’organisation des termes au sein de cette corrélation.
- Note de bas de page 29 :
-
Corrélation sert à introduire les formules où apparaît le symbole ≅ . Par exemple « Une corrélation existe ainsi entre les deux plans » introduit une formule de corrélation proportionnelle (Ibid., p. 187). À certains endroits, l’embrayage est équivoque et semble permettre la confusion entre ≅ et vs : « l’analyse sémique permettra de voir en lui, en corrélation avec l’avant vs l’après narratifs, comme consommateur », à la suite de quoi est produite une formule où avant et après ne sont pas en rapport d’opposition (symbole vs) mais entrent eux-mêmes dans une corrélation proportionnelle (symbole ≅) (Ibid., p. 194). À d’autres endroits, il est clair que les corrélations ne sont pas toujours proportionnelles et que leur correspondent des formules où le symbole ≅ se place entre deux termes au lieu d’être placé entre deux rapports, comme c’est le cas dans les corrélations proportionnelles ; exemple : « […] ce qui permet de supposer la corrélation du père et de l’eau malfaisante » (Ibid., p. 208). Il faut noter enfin que A. J. Greimas et Joseph Courtés (Sémiotique. Dictionnaire raisonné de la théorie du langage (1979), Hachette, coll. Université, 1993, p. 75) donnent à l’entrée de corrélation deux acceptions ; la première est l’acception hjelmslevienne tandis que selon la seconde « le mot de corrélation désigne le plus souvent en sémiotique la relation entre des relations, ces dernières pouvant être constitutives soit de paradigmes, soit de syntagmes ». Comme, dans l’article examiné, on trouve des corrélations qui ne sont pas des relations entre relations, il n’est pas permis de trancher en faveur de cette seconde acception. Aussi, le doute demeure.
Il n’est pas certain toutefois que Greimas, en employant le terme de corrélation dans cet article29, se réfère à la définition qu’en donne Hjelmslev. Le symbole utilisé dans les formules qui se rapportent auxdites « corrélations » tendrait plutôt à indiquer un emprunt auprès de Lévi-Strauss, chez qui l’on trouve des formules telles que
F x (a) : F y (b) ≅ F x (b) : F a-1 (y)
- Note de bas de page 30 :
-
Claude Lévi-Strauss, Anthropologie structurale (1958), Plon, 1974, p. 252.
Fig. 10 - Relations canoniques (Lévi-Strauss, Anthropologie structurale30)
Il est intéressant de signaler en outre que Nicolas Ruwet, dans la traduction de l’article de Jakobson & Halle « Phonologie et Phonétique » parue en 1963, est amené à rédiger une note justifiant par un emprunt à Lévi-Strauss une notation formulaire :
- Note de bas de page 31 :
-
In Roman Jakobson, Essais de linguistique générale, Éditions de Minuit, 1963, p. 104. On trouverait dans les Selected Writings (La Haye, Mouton, 1962), à l’instar de ce nous avons remarqué dans Anthropologie structurale, des symboles de substitution à : : , en particulier le signe de l’égalité ( = ). Jakobson présente les formules sous des expressions telles que « jeu de rapports » [set of ratios] (ibid., p. 420), « équivalence » (ibid., p. 518), ou encore il cite Reformatskij les désignant comme des « relations mutuellement proportionnelles » (ibid., p. 644).
NDT : Nous reprenons cette notation à Cl. Lévi-Strauss (cf. « La Geste d’Asdiwal », Les Temps Modernes, mars 1961) : A : B : : C : D doit se lire A est à B comme C est à D31.
- Note de bas de page 32 :
-
Par exemple dans C. Lévi-Strauss, Mythologiques, 1 : Le cru et le cuit, Plon, 1964, p. 102.
Et l’on trouve bien, en effet, dans d’autres ouvrages, des formules où un couple de deux-points ( : : ) se substitue en lieu et place de ≅32.
- Note de bas de page 33 :
-
A. J. Greimas, Du sens, op. cit., p. 129.
La même année, dans un article en hommage à Dumézil (« La mythologie comparée ») où peine est prise de préciser d’emblée qu’il est antérieur à la parution des Mythologiques de Lévi-Strauss, Greimas emploie déjà le symbole ≅, mais il utilise également, distinctement, un tilde isolé — ~ — comme symbole de comparaison, comparaison qui s’effectue aussi bien entre termes qu’entre rapports33 :
Fig. 11 - « Série comparative » du contrat social dans trois récits mythiques (Greimas, Du Sens)
Aussi la présente formule peut-elle se lire exactement à la manière dont Ruwet présente les proportions de Jakobson : Vena est à Prthu comme Tarquin est à Servius et comme Bress est à X. Une question pendante serait de savoir comment lire distinctement les formules où le symbole ≅ remplace le symbole ~ .
- Note de bas de page 34 :
-
À noter qu’en logique ce symbole peut, aux côtés de ≡ et ⇔, désigner une équivalence. Toutefois, et en dépit d’une manifestation de ce terme (Sémantique structurale, op. cit., p. 156), Greimas ne mentionne pas qu’il emploie ce symbole selon la fonction que celui-ci connaît en logique.
- Note de bas de page 35 :
-
A. J. Greimas, Du Sens, op. cit., p. 228.
Dans ce parcours à travers quelques-uns des premiers textes de Greimas, on se sera ainsi aperçu que la modélisation traverse trois formes sémiotiques — le langage verbal, le langage symbolique et le langage graphique. Deux formats — le graphique et la formule — sont utilisés dans le but de mettre en place un moyen de réflexion (une pensée et une expression pour cette pensée) propre à l’approche sémiotique. Chemin faisant, plusieurs symboles entrent en concurrence recherche — symboles d’opposition (vs), de comparaison (~) et un troisième qui, faute de détermination verbale, sera provisoirement qualifié de « corrélation » (≅)34. Cette concurrence se retrouve dans la multiplicité des références aux théories antérieures, et s’explique en partie à partir d’elle : Hjelmslev fournit notamment à Greimas un modèle graphique d’analyse formelle du contenu ainsi qu’une théorie des rapports ; Lévi-Strauss, des domaines d’application déjà largement travaillés dans le sens de sa propre réflexion ; Jakobson, des présentations formulaires et une théorie des oppositions. Tout cela concourt à la présentation d’un graphique qui connaîtra un impact notable sur la sémiotique. Il s’agit donc d’un premier carré sémiotique, à tout le moins d’une première esquisse de ce carré35 :
Fig. 12 - Structuration de la culture « naturelle » des Bororo (Greimas, Du Sens)
Commençons par observer que l’objet mis sous nos yeux est effectivement un graphique : il comporte des cases dont le format carré n’est pas insignifiant et des flèches qui ne peuvent pas être rapportées à des symboles logiques mais qui sont placées de manière à présenter sur la page une relation entre deux termes, la relation étant elle-même à chaque fois nommée. Il comporte en outre des symboles alphabétiques et des éléments verbaux non syntagmatisés (non syntagmatisés, veux-je dire, suivant les règles syntagmatiques de la langue écrite). Par ailleurs, ce graphique n’est pas un tableau, car il n’enregistre en ses lignes ni en ses colonnes de dénominateur commun à ses cases. Les éléments graphiques employés, les flèches en particulier, permettent de le ranger dans la catégorie des schémas. Son motif essentiel, toutefois, ne réside pas dans les fonctions les plus couramment affectées aux schémas. Ce qui importe, en effet, dans le présent graphique, ce qu’il fait voir instantanément, c’est le nombre de ses cases. Pour cette raison, le graphique auquel il pourrait être le plus apparenté, dans le corpus étudié jusqu’à présent, est le schéma à trois cases de Hjelmslev (Fig. 3). Cet apparentement est bien sûr d’une importance certaine pour le parcours de la réflexion sémiotique. De fait, il apparaîtra bientôt que, élevés au statut de modèles généraux, le schéma à trois cases de Hjelmslev et le carré sémiotique esquissé par Greimas portent sur le même objet, à savoir la structure formelle du sens ; et que, de ce fait, il y a continuité, et transformation apportée dans cette continuité, l’une comme l’autre nettement perceptibles, de la théorie hjelmslevienne à la théorie greimassienne.
Je me borne à pointer pour le moment un seul aspect de la transposition entre les deux théories. Elle concerne, ainsi que l’avait annoncé l’examen des graphiques hjelmsleviens, la binarité. Dans le présent carré sémiotique, la binarité est omniprésente :
-
dans les oppositions duelles de M et non M, et de V et non V, oppositions marquées à la fois par l’emplacement graphique de ces termes et par leurs corrélations en tant qu’éléments de langue : sur le plan de contenu, M reçoit par catalyse un sème de positivité ; sur le plan de l’expression, la présence ou l’absence de non est un marqueur de binarité ;
-
dans la dichotomisation graphique de ciel et eau, et de ciel et terre, alors qu’en langue leur opposition deux à deux n’est pas fortement marquée sur le plan du contenu (et nullement sur le plan de l’expression) ; cette dissociation entre l’effet dichotomisant du graphique et une corrélation non dichotomisante en langue, au lieu de créer une équivoque, renforce le travail de binarisation mis en œuvre ;
-
par la présence de deux termes opposés (conjonction et disjonction) et par leur juxtaposition syntagmatique (qui les montre comme opposés) ;
-
par la présence exclusive, par paires d’identiques, de flèches doubles.
Cependant, par rapport à tous les autres graphiques et formules du corpus que nous avons pas à pas découvert, le graphique du carré sémiotique ne se contente pas de présenter la binarité : bien davantage il l’exprime tout entier, il la fait voir, et même peut-on dire qu’il la ceinture. En vertu de la disposition de quatre cases carrées disposées de telle manière à former ensemble un grand carré, les rapports entre ces cases sont duels dans toutes les directions — à l’horizontale, à la verticale et en diagonales. Et les flèches qui encadrent ce carré accentuent encore sa quadrature. Ainsi ce graphique résout le problème que posaient tant les formules, où sont utilisés soit le symbole vs soit le symbole ≅, que les graphiques de type arbre ou de type tableau : la binarité qui y est présentée ne peut plus dégénérer en série ouverte. Il ne montre au contraire que deux niveaux (supérieur et inférieur, ou gauche et droit), à l’intérieur de chacun desquels règne la loi de la binarité. En outre, comparé au schéma à trois cases de Hjelmslev, il est manifeste que le carré sémiotique fait bien mieux voir son objet, les moyens graphiques s’accordant aux corrélations entre les éléments verbaux que le graphique contient, et même pouvant s’imposer à ceux-ci quand la binarité de leurs corrélations n’est pas assurée (le cas de ciel et eau).
Remarque : il ne s’agit évidemment pas ici de prétendre que la théorie greimassienne se montre supérieure à la théorie hjelmslevienne, mais seulement que les moyens graphiques qu’elle met en œuvre le sont, eux, supérieurs, en raison de leur plus grande adéquation au regard de l’objet théorique qu’ils présentent.
Greimas & Rastier
- Note de bas de page 36 :
-
Repris dans A. J. Greimas, Du Sens, op. cit.
Une transposition de la formule de corrélation proportionnelle vers le carré sémiotique est établie explicitement dans l’article écrit « en collaboration avec François Rastier » où s’instaure une modélisation théorique à portée générale (« Les jeux des contraintes sémiotiques », de 196836). La formule est en outre introduite par une phrase qui apporte un supplément à sa qualification :
- Note de bas de page 37 :
-
Ibid., pp.137-138.
Celle-ci [la structure déjà présente, mais différemment, dans le carré sémiotique] apparaît alors comme la mise en corrélation de deux catégories couplées, la corrélation elle-même se définissant comme une relation de contradictions homologuées37 :
Fig. 13 - Structure d’homologation (Greimas, Du sens)
- Note de bas de page 38 :
-
Ibid., p. 150.
Dans l’appareil définitionnel de Hjelmslev, la corrélation (paradigmatique) était distincte de la relation (syntagmatique). On voit que la seconde acception du terme de corrélation rapportée dans le dictionnaire Sémiotique (et reproduite ici dans la note 28), où la corrélation est d’application tant dans les paradigmes que dans les syntagmes, doit finalement être privilégiée, bien que le rapprochement graphique que nous avions aperçu entre le schéma à trois cases et le carré sémiotique (son esquisse) pouvait se fonder sur une définition commune de la corrélation chez les deux auteurs (le doute était donc lui-même fondé). Pour autant, l’application de cette seconde acception ne laisse pas de faire difficulté, même au sein du seul article de 1968. Car on y trouve des symboles de corrélation qui ne sont pas posés entre des contradictions, c’est-à-dire qui ne présentent pas des relations de relations, mais qui sont posés entre des symboles alphabétiques (des termes), qui plus est nullement présentés comme des contradictoires, tel par exemple, à l’intérieur d’un paragraphe : « c1 ≅ p2 »38. Aussi l’élément réellement neuf de la qualification apportée par la phrase d’introduction citée est-il le terme d’homologation. Une corrélation ne peut être qu’une relation d’homologation, car les contradictions homologuées ne le sont qu’en vertu de cette relation. De plus, la détermination de la corrélation par l’homologation permet de suspendre la difficulté qui vient d’être évoquée : une homologation peut aussi bien jouer entre des relations qu’entre des relata. On tiendra donc à présent pour établi que la fonction à laquelle renvoie le symbole ≅ est la fonction d’homologation. Or il y a quelque chose d’intéressant à signaler à propos de l’homologation (et de son symbole) : c’est que, contrairement à toutes les autres fonctions qui ont servi dans les formules proposées jusqu’ici par Greimas, celle-ci ne connaît pas d’usage en logique. Si la fonction d’homologation doit être consacrée, ce ne pourra être que par le fait de la théorie sémiotique.
Il importe alors de préciser si elle est entièrement due à l’inventivité de Greimas ou si elle peut être comprise dans un parcours d’élaboration théorique plus étendu que la seule œuvre, commençante, de Greimas. À cette question, Greimas apporte lui-même un début de réponse, en présentant la structure d’homologation comme un modèle applicable à des travaux antérieurs. Le paragraphe suivant la formule déjà reproduite ci-dessus mérite d’être cité intégralement :
- Note de bas de page 39 :
-
Ibid., p. 138.
Cette nouvelle présentation permet de voir que la structure qui permet de rendre compte du mode d’existence de la signification trouve son application, en tant que modèle constitutionnel des contenus investis, dans des domaines fort variés : c’est, en effet, aussi le modèle du mythe proposé par Lévi-Strauss, et la forme de l’articulation achronique du conte populaire, et encore le modèle justifiant un certain nombre d’univers sémantiques particuliers (Bernanos, Mallarmé, Destutt de Tracy). Il est réconfortant pour le sémioticien de constater qu’une démarche déductive rencontre sur son chemin des modèles construits empiriquement pour rendre compte de corpus limités39.
- Note de bas de page 40 :
-
In Vladimir Propp, Morphologie du conte, Seuil, coll. Points, 1970, p. 221. Il ajoute à la suite que « dans son analyse du mythe, au contraire, il part de Lévi-Strauss, en le complétant par la théorie de Propp », mais ce complément ne prend nullement l’aspect d’une modélisation. Il n’y a pas de symétrie dans les emprunts faits par Greimas à ces deux auteurs.
Greimas s’est ainsi trouvé des contributeurs pour l’élaboration de ce modèle d’homologation, et l’un d’entre eux au moins, Vladimir Propp, pourrait l’être à titre de précurseur. Mais les différences perceptibles entre les formulations verbales qui se rapportent à l’un ou à l’autre de ces contributeurs sont significatives. Quant à Lévi-Strauss, Greimas reconnaît explicitement que sa démarche est analogue à celle de l’anthropologue. C’est ce que nous avons pu vérifier : le modèle d’homologation est bel et bien présent dans l’œuvre de Lévi-Strauss (cf. Fig. 10), quoique Greimas l’interprète diversement selon les cas, soit comme un modèle de « série comparative » (symbole ~) soit comme ledit modèle d’homologation (symbole ≅). Par contre, en ce concerne Propp, Greimas ne dit pas que celui-ci soit parvenu à une modélisation analogue, mais que les formes de son objet empirique peuvent correspondre à cette modélisation. De fait, si l’on trouve un certain nombre de graphiques et de formules dans Morphologie du conte, aucun d’entre eux ne présente une structure d’homologation ou quoi que ce soit qui s’y apparenterait. Comme l’écrit E. Mélétinski en postface à la traduction française : « Dans son analyse du conte, Greimas prend pour base Propp, en le complétant et en le ‘corrigeant’ par la théorie de Lévi-Strauss »40. Ceci s’applique a fortiori lorsque le modèle permet de « justifier » des univers sémantiques préalablement étudiés. Ces études ne renvoient d’ailleurs qu’à des travaux antérieurs de Greimas (pour Bernanos) et de Rastier (pour Destutt de Tracy) ainsi, sans doute, qu’à L’Univers imaginaire de Mallarmé de Jean-Pierre Richard. Ainsi, en dehors de l’influence à Lévi-Strauss, déjà examinée plus haut, l’homologation et sa formule générale sont bien dues à Greimas et ne peuvent pas véritablement être rattachées à une tradition théorique.
Il reste à déterminer si cette structure d’homologation a connu des modifications d’un texte à l’autre. Il suffit de comparer les figures 7 et 13 pour s’en aviser. Certes, les deux figures ne prétendent pas présenter le même objet : dans Fig. 7, le symbole p a pour objet une fonction narrative particulière (i.e. fonction de retour du héros dans le conte populaire russe), tandis que dans Fig. 13 le symbole s1 a pour objet un sème, déterminé (s1 appartient à l’axe sémantique S) mais général (s1 comme S renvoient à des concepts). Pour autant, rien n’empêche de se demander si leur structure d’homologation est identique. L’est-elle ? Seulement à condition de donner s2 pour équivalent à non p. De Fig. 7 à Fig. 13, il y a donc une perte, qui réside dans la qualification du rapport entre s1 et s2, Fig. 13 se bornant à établir ce rapport (par l’adjonction d’indices numériques distincts à un même symbole alphabétique) sans le qualifier, alors que non, dans le symbole « non p » manifesté dans Fig. 7, a naturellement un signifié isolable. C’est au texte qu’il revient de combler ce manque : s1 et s2 sont établis comme des sèmes contraires, par quoi il est aisé de reconnaître que s2 est bien équivalent à non s1.
- Note de bas de page 41 :
-
A. J. Greimas, Du Sens, op. cit., p. 137.
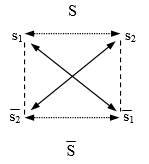
On en vient alors au carré sémiotique qui, dans l’article de Greimas & Rastier, aura été présenté d’abord41 :
Fig. 14 - « Structure élémentaire de la signification » (Greimas, Du Sens)
La relation de contrariété existant entre s1 et s2 est présente dans le graphique que constitue le carré sémiotique grâce à la présence d’une double flèche en pointillé. La relation de contradiction existant entre s1 et 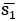 , d’une part, s2 et
, d’une part, s2 et 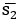 , d’autre part, est manifestée quant à elle deux fois : par l’usage d’un symbole spécifique ( – , soit une petite barre horizontale placée au-dessus du symbole alphabétique) et par une double flèche (en ligne pleine). Ces relations sont également établies dans la structure d’homologation et, selon Fig. 7, elles sont toutes deux manifestées dans le format formulaire (la formule de Fig. 13 ne présentant, pour sa part, que la relation de contradiction). Il se confirme ainsi que le carré sémiotique est une transposition dans un format graphique d’une structure présentée d’abord selon un autre format.
, d’autre part, est manifestée quant à elle deux fois : par l’usage d’un symbole spécifique ( – , soit une petite barre horizontale placée au-dessus du symbole alphabétique) et par une double flèche (en ligne pleine). Ces relations sont également établies dans la structure d’homologation et, selon Fig. 7, elles sont toutes deux manifestées dans le format formulaire (la formule de Fig. 13 ne présentant, pour sa part, que la relation de contradiction). Il se confirme ainsi que le carré sémiotique est une transposition dans un format graphique d’une structure présentée d’abord selon un autre format.
- Note de bas de page 42 :
-
On trouve, il est vrai, dans l’article de 1966, mais seulement dans le commentaire qui suit l’esquisse de carré sémiotique, une notation formulaire « non M M » paraphrasée comme une « relation de subordination culturelle » (ibid., p. 228). Aucune précision ne vient préciser la place théorique de cette relation pour le reste inédite.
- Note de bas de page 43 :
-
Jacques Fontanille & Claude Zilberberg (Tension et signification, Liège, Mardaga, 1998, p. 48) font une hypothèse légèrement différente, mais entièrement compatible, en renvoyant au dernier chapitre de l’ouvrage, c’est-à-dire probablement, et plus précisément, au « modèle constitutionnel » que représente la formule produite à la page 233, laquelle est pratiquement identique à celle de la page 198 (seules les lettres y sont différentes, ainsi que leur disposition).
Mais, par ailleurs, le carré sémiotique présente une relation qui n’était apparue nulle part ailleurs42 : une relation d’implication existant s1 et 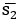 , d’une part, s2 et
, d’une part, s2 et 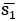 , d’autre part. Dans une remarque qui suit la présentation du carré sémiotique, Greimas & Rastier insèrent une remarque stipulant que « le modèle ci-dessus n’est qu’une reformulation remaniée de celui qui a été proposé antérieurement (Greimas, Sémantique structurale, 1966, Larousse) » mais l’on se trouve bien en peine, faute de renvoi à une page précise, de savoir où chercher exactement ce modèle, Sémantique structurale ne présentant aucun graphique ressemblant au carré sémiotique. L’hypothèse à laquelle nous invite la formule présentée à la suite du carré (notre Fig. 13) renverrait alors justement à la formule contenue à la page 198 de cet ouvrage, celle dont il vient encore d’être question ici (c’est notre Fig. 7)43. Sémantique structurale, sauf erreur de ma part, ne parle jamais de relation d’implication entre termes d’un système sémique. On peut y lire en revanche qu’une relation d’implication existant entre fonctions narratives (non s → s)
, d’autre part. Dans une remarque qui suit la présentation du carré sémiotique, Greimas & Rastier insèrent une remarque stipulant que « le modèle ci-dessus n’est qu’une reformulation remaniée de celui qui a été proposé antérieurement (Greimas, Sémantique structurale, 1966, Larousse) » mais l’on se trouve bien en peine, faute de renvoi à une page précise, de savoir où chercher exactement ce modèle, Sémantique structurale ne présentant aucun graphique ressemblant au carré sémiotique. L’hypothèse à laquelle nous invite la formule présentée à la suite du carré (notre Fig. 13) renverrait alors justement à la formule contenue à la page 198 de cet ouvrage, celle dont il vient encore d’être question ici (c’est notre Fig. 7)43. Sémantique structurale, sauf erreur de ma part, ne parle jamais de relation d’implication entre termes d’un système sémique. On peut y lire en revanche qu’une relation d’implication existant entre fonctions narratives (non s → s)
peut être transformée, du fait de l’existence, dans le contenu sémique des fonctions couplées, d’une relation de disjonction, en
s vs non s,
- Note de bas de page 44 :
-
A. J. Greimas, Sémantique structurale, op. cit., p. 204 ; la présentation formulaire est de Greimas ; par contre c’est moi qui souligne : le syntagme souligné est identique au titre de la section où est présenté le carré sémiotique dans l’article de Greimas et Rastier.
permettant la saisie du couple fonctionnel en tant que structure élémentaire de la signification »44.
Le carré sémiotique apparaît ainsi comme un moteur de découverte théorique. On peut en effet faire raisonnablement l’hypothèse que c’est la disposition graphique, et la présence des relations préexistantes de contrariété et de contradiction, qui a permis l’émergence de la relation d’implication. Cette hypothèse va recevoir une série de confirmations.
D’abord, la comparaison du carré sémiotique avec son esquisse (Fig. 12) dénote l’approfondissement d’une pensée inhérente à la présentation graphique. Les flèches, dans l’esquisse, restaient sous la coupe d’une indexation verbale et n’étaient pas elles-mêmes différenciées. Cette indexation verbale présupposait ainsi une argumentation non contenue dans le graphique et seule susceptible d’établir que le rapport désigné par ces flèches fût de « disjonction – conjonction », de « conjonction – disjonction », ou de « disjonction » seulement (et un passage verbal vient d’être cité, dans le paragraphe précédent, où transparaît cette argumentation). Dans le présent carré sémiotique, les flèches sont au contraire différenciées par des moyens graphiques et renvoient de ce fait en elles-mêmes à des objets distincts (i.e. à trois types de relations). Or c’est bien le graphique qui suscite cette différenciation : la binarité pousse à ce que chaque élément graphique y trouve un seul identique ; ainsi des flèches, mais aussi des indices et des symboles de contradictoire ( – ). L’approfondissement de la pensée graphique présuppose évidemment que celle-ci soit reconnue en tant que telle — et nous trouvons ainsi une première preuve de l’effectivité de la modalité épisémiotique à l’œuvre dans les graphiques. Dans le cas présent, c’est ce que j’ai appelé le « bouclage » de la binarité — bouclage qui n’est manifesté que dans et par les graphiques, jamais dans les formules, encore moins dans les propositions verbales — qui, par son maintien d’un graphique à l’autre, est l’indice d’un faire auto-présentatif. J’entends par là qu’en présentant son objet (la structure élémentaire de la signification) le carré sémiotique se présente comme étant devenu la forme même de cette structure.
- Note de bas de page 45 :
-
A. J. Greimas, Du Sens, op. cit., p. 139.
Ensuite, les relations d’implication, telles qu’elles sont présentées par des flèches dans le carré sémiotique, affranchissent celui-ci de difficultés théoriques auxquelles avaient conduit les emprunts de Greimas à ses prédécesseurs. En particulier, elles suspendent la difficulté théorique qu’il y aurait à concilier les propositions greimassiennes avec les définitions hjelmsleviennes. Nous avons vu que les usages du concept de corrélation par Greimas n’étaient pas entièrement compatibles avec l’acception hjelmslevienne de ce concept, bien que Greimas ait cherché à les y rapporter. L’homologation apparaissait alors comme le moyen de suspendre, dans les formules, cette difficile conciliation. Une difficulté similaire apparaît à présent pour la contrariété. Dans Sémantique structurale, celle-ci ou bien est liée à une opposition ou bien entre dans une corrélation, c’est-à-dire qu’elle est associée à des fonctions paradigmatiques. Dans l’article de Greimas & Rastier, elle est au contraire explicitement définie comme une relation, et les auteurs ajoutent que « dans les termes de Hjelmslev, elle peut être identifiée comme la solidarité, ou double présupposition »45, c’est-à-dire que la contrariété devient une fonction syntagmatique. Or le carré sémiotique permet d’affranchir la contrariété d’une détermination paradigmatique ou syntagmatique ; partant, il permet de dépasser la possibilité d’une contradiction, à tout le moins d’une difficulté théorique. Il permet en outre de considérer trois types de « rapport », dont deux peuvent être raisonnés par la typologie hjelmslevienne des relations syntagmatiques (contrariété et implication, respectivement, en termes hjelmsleviens : solidarité et sélection) mais certainement pas le troisième (la contradiction) qui, si elle est considérée comme relation (et tel est bien le cas), ne peut pas l’être par recours à la théorie de Hjelmslev. Le rapport de contradiction demande alors la constitution d’une autre typologie, où il peut être distingué, selon un autre critère, de l’implication et / ou de la contrariété. Ce critère, le texte ne le fournit pas. Le carré sémiotique permet en effet de s’en passer : trois types de rapport sont établis tout simplement parce qu’il y a dans le carré trois directions pour relier un terme à un autre.
- Note de bas de page 46 :
-
Oserait-on dire que la sémiotique et la logique sont en relation de contrariété ? Il faudrait pour cela que la logique « ait besoin » d’une sémiotique distincte d’elle-même, ce qu’elle conteste.
Naturellement, le rapport d’implication, et sa détermination en tant que tel, ne sortent pas de nulle part. Le carré sémiotique a, on le sait, un ascendant dans une discipline dont la sémiotique aura constamment cherché à se distinguer46 ; je veux évidemment parler du carré logique :
- Note de bas de page 47 :
-
Th. De Praetere, Théorie de l’argumentation et éléments de logique [en ligne], 1998, <http://www.icampus.ucl.ac.be/DROI1111/document/logique/4bINFI.htm>
Fig. 15 - Carré logique (De Praetere, Théorie de l’argumentation et éléments de logique47)
- Note de bas de page 48 :
-
A. J. Greimas, Du Sens, op. cit., p. 137.
- Note de bas de page 49 :
-
Au demeurant, il est piquant d’observer que la recommandation de comparaison, en ce qui concerne la discipline de la logique, mentionne un hexagone, alors que la carré logique offre évidemment bien plus de points possibles de rapprochement. Il n’y a sans doute là guère davantage qu’une manœuvre rhétorique dans l’argumentation de Greimas & Rastier… à moins que les auteurs aient retenu l’hexagone de Blanché parce qu’une relation y est désignée sous le terme d’implication, quoique celle-ci se manifeste six fois, sans rapprochement plausible avec la relation d’implication stipulée dans le carré sémiotique.
Il est clair que les symboles A, E, I, O n’ont pas en logique les mêmes objets que ceux présentés par les symboles utilisés dans le carré sémiotique. Ils ne présentent non plus entre eux de rapport symbolique, alors qu’un tel rapport, et même plusieurs d’entre eux, peuvent être trouvés, en fonction des indices et des symboles de contradictoire, entre les symboles alphabétiques du carré sémiotique. Néanmoins, la disposition en carré, la présence de rapports schématiques (ici présentés par des éléments verbaux disposés de manière linéaire entre les symboles alphabétiques) et l’indexation identique de deux de ces rapports (contraires et contradictoires) suffisent à rendre effectif le rapprochement. De quel ordre exactement est alors ce rapprochement ? Il repose pour l’essentiel sur l’expression graphique, non sur les objets présentés. Sur le plan du contenu, il confirme l’observation générale que ce que font voir les graphiques sémiotiques, c’est précisément le caractère sémiotique de leurs objets. Le rapprochement entre le carré logique et le carré sémiotique implique en effet que les relations, et la structure qu’elle instaure, sont plus fondamentales que les relata, ce qui est le credo de toute approche structuraliste, en général, et celui de la sémiotique continentale en particulier. Le carré sémiotique ne fait pas voir autre chose que cette structure. Et, lorsque Greimas & Rastier recommandent de comparer le carré sémiotique à l’ « hexagone logique de R. Blanché […] ainsi qu’aux structures désignées en mathématiques, comme groupe de Klein, et, en psychologie, comme groupe de Piaget »48, ce qui est immédiatement comparable est bien encore, comme ils l’écrivent, la structure de ces conceptualisations théoriques, dont l’un des comparants est d’ailleurs désigné d’après son format graphique (un hexagone49).
- Note de bas de page 50 :
-
Rappelons qu’il est arrivé à Greimas de parler précédemment de relation de subordination (cf. note 28).
Pour revenir à la relation d’implication, on remarque qu’elle est absente du carré logique, qui instaure en sa place une relation de sulbalternation50. Une chose est à noter quant à cette relation logique : elle n’est pas réciproque, mais elle ne propose pas non plus un seul parcours. Selon la logique des propositions, la relation peut se faire en effet dans l’un et l’autre sens, mais non pour le même type d’assertion. Des schémas permettent de visualiser ces deux parcours :
Fig. 16 & 17 - Inférences valides de sulbalternation (De Praetere, Théorie de l’argumentation et éléments de logique)
- Note de bas de page 51 :
-
A. J. Greimas, Du Sens, op. cit., p. 137, n. 1.
Ainsi, par exemple, dans le premier schéma, A → I peut se lire : S’il est vrai que tout S est P, alors il est vrai que quelque S est P, tandis que, dans le second schéma, E ← O se lira : S’il est faux que quelque S n’est pas P, alors il est faux qu’aucun S n’est P. De Praetere fait remarquer que « la fausseté monte et la vérité descend », ce qui fera peut-être sourire le sémioticien sensible à l’analyse des connotations. Or, dans une note relative à la relation d’implication, Greimas & Rastier reconnaisse que « si l’existence de ce type de relation paraît indiscutable, le problème de son orientation (s1 → 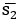 ou
ou 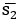 → s1) n’est pas encore tranché. On s’abstiendra d’en parler, sa solution n’étant pas exigée par la suite de la démonstration »51. Nous nous trouvons à nouveau devant une difficulté que le graphique permet non seulement de découvrir, mais également de suspendre dans le temps même de sa découverte. De la présentation des autres relations par des flèches découle naturellement, suivant une pensée graphique, la découverte d’une possibilité d’orientation de la relation d’implication. Or, quelle doit être cette orientation ? Faute de pouvoir le déterminer par la réflexion sémiotique en l’état de sa recherche, faute aussi de pouvoir s’en faire une idée à partir du carré logique, la détermination de l’orientation de l’implication est suspendue, ce que le moyen graphique retenu dans le carré sémiotique fait voir de manière immédiate et évidente.
→ s1) n’est pas encore tranché. On s’abstiendra d’en parler, sa solution n’étant pas exigée par la suite de la démonstration »51. Nous nous trouvons à nouveau devant une difficulté que le graphique permet non seulement de découvrir, mais également de suspendre dans le temps même de sa découverte. De la présentation des autres relations par des flèches découle naturellement, suivant une pensée graphique, la découverte d’une possibilité d’orientation de la relation d’implication. Or, quelle doit être cette orientation ? Faute de pouvoir le déterminer par la réflexion sémiotique en l’état de sa recherche, faute aussi de pouvoir s’en faire une idée à partir du carré logique, la détermination de l’orientation de l’implication est suspendue, ce que le moyen graphique retenu dans le carré sémiotique fait voir de manière immédiate et évidente.
Moteur de découverte, le graphique est ainsi un moyen de pensée pour la sémiotique. Qui plus est, ce qu’il permet de découvrir achemine la recherche sémiotique vers sa spécificité, en permettant par la même occasion de suspendre les problèmes auxquels la confrontent ses emprunts à des sources diverses, et finalement de s’affranchir vis-à-vis de ces sources, non complètement bien sûr, mais suffisamment pour déterminer une approche qui lui soit propre.
Remarque : je tiens à préciser à nouveau que ces observations sur les graphiques sémiotiques, et sur leur impact pour la pensée sémiotique, n’impliquent aucun jugement permettant d’infirmer ou de confirmer la validité des théories sémiotiques et des concepts qui les soutiennent. Tout au plus disent-elles quelque chose sur la légitimité d’une pratique.
Greimas & Courtés
- Note de bas de page 52 :
-
A. J. Greimas & J. Courtés, Sémiotique. Dictionnaire..., op. cit., p. 31.
Il n’y aurait pas matière, face à l’entrée « Carré sémiotique » de Sémiotique. Dictionnaire raisonné de la théorie du langage, à ouvrir une section nouvelle dans cette étude, si ce n’est afin de poser un jalon situé chronologiquement à mi-chemin entre le texte de la section précédente et celui qui fera l’objet de la section suivante. On remarquera néanmoins que la « représentation » y est donnée pour « définitive ». La voici52 :
Fig. 18 - Carré sémiotique (Greimas & Courtés, Sémiotique. Dictionnaire raisonné de la théorie du langage)
- Note de bas de page 53 :
-
A. J. Greimas, Du Sens, op. cit., p. 139.
- Note de bas de page 54 :
-
Ibid. À leurs entrées respectives, le (terme) complexe et le (terme) neutre correspondent bien toutefois aux axes nouvellement déterminés, à cette précision près apportée par les auteurs que des « opérations syntaxiques préalables » auront joué sur eux (A. J. Greimas & J. Courtés, Sémiotique. Dictionnaire..., op. cit., p. 55 et 251).
Par rapport à la précédente version du carré (fig. 14), on observe quelques changements notables. Premièrement, là où Greimas & Rastier avaient suspendu la question soulevée par l’orientation de la relation d’implication, Greimas & Courtés ont quant à eux tranché, et tranché dans le sens d’une montée en force de la fausseté — je plaisante. Deuxièmement, la relation entre s1 et s2 n’est plus reproduite entre 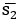 et
et 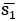 . Une troisième modification intervient dans la légende pour confirmer la deuxième : l’axe
. Une troisième modification intervient dans la légende pour confirmer la deuxième : l’axe 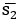 –
– 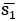 y est tenu pour l’axe des subcontraires, alors que Greimas & Rastier les tenaient dans une relation de contrariété, à l’instar de s1 et s2. Une quatrième modification présente tant dans la figure graphique que dans la légende connaît une certaine répercussion dans la théorie : S et
y est tenu pour l’axe des subcontraires, alors que Greimas & Rastier les tenaient dans une relation de contrariété, à l’instar de s1 et s2. Une quatrième modification présente tant dans la figure graphique que dans la légende connaît une certaine répercussion dans la théorie : S et 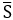 disparaissent, et les axes qu’ils avaient pour objet prennent une toute autre détermination sous la désignation de s1 – s2 et
disparaissent, et les axes qu’ils avaient pour objet prennent une toute autre détermination sous la désignation de s1 – s2 et 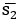 –
– 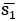 . L’axe s1 – s2 est désormais connu comme axe des contraires, alors qu’il était déterminé comme « axe du complexe » sous la dénomination S53 ; l’axe
. L’axe s1 – s2 est désormais connu comme axe des contraires, alors qu’il était déterminé comme « axe du complexe » sous la dénomination S53 ; l’axe 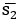 –
– 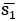 est quant à lui, on vient de le rappeler, l’axe des subcontraires, alors que
est quant à lui, on vient de le rappeler, l’axe des subcontraires, alors que 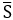 était l’axe du neutre54. Il reste à signaler une dernière modification, si évidente que j’ai failli l’omettre, et dont l’importance ne pourra être mesurée que plus tard : le carré est devenu un rectangle.
était l’axe du neutre54. Il reste à signaler une dernière modification, si évidente que j’ai failli l’omettre, et dont l’importance ne pourra être mesurée que plus tard : le carré est devenu un rectangle.
Si la binarité a pu être verrouillée par le carré sémiotique, il revient également à celui-ci de montrer le moyen de la déverrouiller. Les modifications observées vont toutes dans ce sens. De façon analogue, les questions qu’il permettait de laisser en suspens dans sa précédente version trouvent réponse dans la nouvelle : la relation d’implication y a trouvé son orientation, et la relation de contrariété n’y est plus seulement posée en miroir des relations relevant d’autres types, de sorte que les déterminations syntagmatique et paradigmatique n’ont plus à jouer un rôle distinctif entre elles. Le graphique demeure ainsi un moyen privilégié pour accomplir la pensée sémiotique et pour saisir son cheminement.
Greimas & Fontanille
- Note de bas de page 55 :
-
J’ai compté également 8 formules, quoique certaines d’entre elles fassent jouer des ressorts dont on pourrait argumenter qu’ils appartiennent plutôt aux graphiques (l’allongement des flèches, par exemple).
C’est à nouveau le carré sémiotique que l’on retrouve majoritairement dans Sémiotique des passions. Sur un total de 32 graphiques55, 22 sont des carrés, répartis à peu près équitablement sur les trois chapitres que compte l’ouvrage. Deux types de variantes vont retenir notre attention.
- Note de bas de page 56 :
-
A. J. Greimas & J. Fontanille, Sémiotique des passions, Seuil, 1991, p. 127.
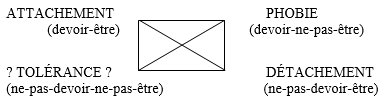
Lorsque les carrés ont pour objet une analyse sémiotique, au lieu d’une analyse métasémiotique (comme c’était le cas dans les exemplaires précédemment examinés ici), les symboles alphabétiques font place à des termes verbaux. Toutefois, on voit alors apparaître quelquefois, en cette place, des points d’interrogation. Ainsi, par exemple56 :
Fig. 19 - « Microsystème sémantique » de l’avarice (Greimas & Fontanille, Sémiotique des passions)
- Note de bas de page 57 :
-
Ibid., p. 132.
Des moyens graphiques, le présent carré sémiotique a réduit l’expression à deux lignes diagonales donnant lieu à une disposition géométrique de termes verbaux à ses extrémités. La figure s’est cependant enrichie par ailleurs de quatre arbres dont chaque terme du carré constitue un des « sommets » (un premier niveau hiérarchique). C’est aux derniers niveaux de ces arbres que l’on trouve, à trois reprises, des points d’interrogation. L’un de ceux-ci disparaît dans le graphique suivant, graphique dont l’objet est identique au précédent57 :
Fig. 20 - Remplissage de la fig. 19 (Greimas & Fontanille, Sémiotique des passions)
- Note de bas de page 58 :
-
Sur les fonctions grammatologiques de l’écriture, voir Jean-Marie Klinkenberg, Précis de sémiotique générale, Bruxelles, De Boeck, 1996, pp. 173-175 et Id., « Vers une typologie générale des fonctions de l’écriture. De la linéarité à la spatialité », Bulletin de la Classe des Lettres XVI-1/6, 2005, pp. 157-196.
Un nota bene précise que « les figures de l’excès sont en italique et les figures de la mesure sont en gras », ce qui permet d’économiser un niveau hiérarchique (le niveau intermédiaire) dans les arbres et de gagner en lisibilité grâce à un moyen grammatologique du langage écrit58. De ce fait, la figure ajoute encore à la polysémioticité des graphiques. On comprend aussi, en comparant les deux graphiques, que l’interrogation stipulée dans la figure 19 par la place circonscrite, aux niveaux supérieurs, grâce à la catégorie d’un « laisser mesuré » a été comblée dans la figure 20 par trois nouveaux termes verbaux, tandis que la catégorie du « donner mesuré » s’est vue quant à elle augmentée, au dernier niveau, d’un deuxième terme verbal (« générosité 1 ») dont le besoin n’avait nullement été pressenti à travers le premier graphique.
- Note de bas de page 59 :
-
A. J. Greimas & J. Fontanille, Sémiotique des passions, op. cit., p. 217 et 222.
D’autres graphiques, dans la troisième partie, sont soumis à des interrogations similaires59 :
Fig. 21 - Microsystème sémantique de la dimension fiduciaire (Greimas & Fontanille, Sémiotique des passions)
Fig. 22 - « Microsystème de l’attachement » (Greimas & Fontanille, Sémiotique des passions)
Par ses mentions entre parenthèses, la dernière figure atteste, au cas l’on en douterait, que ces graphiques sont bien des variantes de carré sémiotique, reliant le terme situé à l’extrémité supérieure gauche aux autres extrémités par deux formes de négation, ainsi que le prescrit le modèle métasémiotique. On repère dans chacun d’eux des points d’interrogation. Que signalent-ils ? Ils indiquent que la place structurelle est présupposée, et le terme susceptible de l’occuper, présupposant. Entre la place structurelle et le terme à tester, plusieurs cas sont envisageables : (i) la structure appelle une réflexion sémiotique qui aboutit à l’adéquation d’un objet désigné par un terme verbal, comme dans la figure 20 ; (ii) la structure laisse une place pendante, occupée artificiellement (c’est-à-dire, sans objet attesté) par un néologisme (figure 21) ; (iii) la structure fait coïncider une place avec un objet, tout en laissant subsister un doute sur leur adéquation l’un vis-à-vis de l’autre (l’adéquation pouvant en effet s’éprouver dans les deux sens : du concept structurel à l’objet attesté, ou de l’objet vers le concept) ; ce dernier cas est celui que rencontre la figure 22. On reconnaît dans les trois cas le principe de découverte mis à l’œuvre dans et par les graphiques.
On reconnaît même davantage : que la structure connaît une existence graphique, conceptuellement graphique, pouvant se passer d’éléments à structurer. Cette capacité des graphiques à présenter une structure sans ses éléments, une relation sans ses relata, fait défaut à la langue verbale, avec tous les problèmes que cela occasionne pour tous ceux, du philosophe au linguiste, qui cherchent à décrire de telles structures et relations. Je ne sais si cette observation suffit à réfuter l’hypothèse faite par Hjelmslev, et souvent relayée depuis, que la langue sert de métalangage universel. Elle incite en tout cas à la nuance. Les graphiques sont capables de nous faire voir des choses que la langue arrive difficilement, ou avec hésitation, à exprimer.
- Note de bas de page 60 :
-
Ibid., p. 219.
L’autre type de variante du carré sémiotique qui doit retenir notre attention n’est manifesté dans Sémantique des passions que par un seul exemplaire, mais il sera amené, par la suite, à connaître un développement considérable. En bref, disons que ce qui se met alors en place va bientôt contribuer pleinement à l’évolution de la réflexion sémiotique entamée par le carré sémiotique. Voici cet exemplaire60 :
Fig. 23 - Parcours de la jalousie (Greimas & Fontanille, Sémiotique des passions)
La figure 21 peut en témoigner : cette nouvelle figure découle bien d’un carré, dont elle conserve trois éléments verbaux et deux lignes, lignes auxquelles elle ajoute des directions (ce sont à nouveau des flèches) et dans lesquelles elle insère des éléments verbaux qui ne sont manifestement pas des index (puisque deux de ces éléments se rapportent à une seule flèche). Le graphique a pour objet un parcours, qu’il fait voir en effet, selon les normes standard de lecture (c’est-à-dire en partant de l’élément verbal situé le plus à gauche dans la zone supérieure) et selon des moyens schématiques simples (deux flèches), et au cours duquel des éléments verbaux sont donnés à lire.
- Note de bas de page 61 :
-
Cette diversité est sans doute imputable au caractère collectif de l’ouvrage, considération qui n’entre pour rien dans la présente analyse (il ne s’agit que d’y constater des possibles, non d’y expliquer des faits).
La coïncidence entre la disposition des éléments qu’elle emprunte au carré sémiotique et celle de ces mêmes éléments dans ledit carré n’est assurément pas fortuite, mais elle n’est pas non plus nécessaire à son objet. Dans d’autres cas, en effet, à partir d’un carré sémiotique, les auteurs ont préféré présenter le parcours sous l’aspect d’une formule61, telle par exemple :
- Note de bas de page 62 :
-
A. J. Greimas & J. Fontanille, Sémiotique des passions, op. cit., p. 142.
Fig. 24 - « Parcours existentiel » du sujet passionné (Greimas & Fontanille, Sémiotique des passions62)
où la présentation formulaire accuse, il est vrai, une tendance au formatage graphique (allongement des flèches et des espaces, juxtaposition de deux lignes d’éléments verbaux à la manière d’un tableau). La seconde ligne explicite le contenu structurel de l’objet, conforme à un carré sémiotique présenté à la page précédente. Le lien avec un carré sémiotique reste donc fort, mais il n’est pas marqué par la présentation qui en est faite.
Par comparaison, dans la figure 23, il y a, pour ainsi dire, « rémanence » du carré sémiotique, ainsi qu’on le dit d’une figure qui s’imprime sur une surface après qu’il a été exposé à une forte lumière. La raison d’une telle impression est simple : le carré sémiotique est devenu un format graphique à part entière. Il en possède désormais tous les attributs : (i) il est analysable en éléments graphiques (des formants) ; (ii) il est immédiatement reconnaissable ; (iii) il se manifeste par des variantes en vertu desquelles il est éprouvé comme une constante (si l’on préfère : comme un type) ; (iv) il est réalisé par des figures où les formants graphiques composent avec des formants appartenant à d’autres sémiotiques. Plusieurs circonstances permettent d’expliquer cette promotion : la fréquence de ces réalisations, son éloignement des formats graphiques disponibles (jusqu’ici il avait été tenu, faute de mieux, pour un schéma), une désignation et une référenciation verbale récurrentes en tant que carré sémiotique, une puissance épisémiotique éprouvée, enfin une variabilité de manifestations suffisamment large pour mettre en valeur la « rémanence » d’un type.
- Note de bas de page 63 :
-
On notera que la distinction entre sens et direction s’avère ici nécessaire : le sens se détermine d’un point vers un autre point, la direction par une ligne (par rapport à d’autres lignes).
La variante examinée est toutefois si éloignée des variantes ordinaires du carré qu’il devient possible et légitime de se demander si une limite n’a pas été franchie au-delà de laquelle la possibilité d’un autre format en devenir est ouverte. La logique graphique à l’œuvre dans la présentation d’un parcours oblige en effet à modifier celle du carré. Dans le carré, les relations entre les termes, même à admettre qu’elles seraient des relations syntagmatiques, ne sont pas temporalisées ; elles demeurent catégorielles, c’est-à-dire qu’elles instaurent une hiérarchie. Avec la figure 23, en revanche, nous nous trouvons devant des relations où le facteur temporel entre en compte, et dans l’objet présenté (il s’agit d’un parcours), et dans sa présentation (selon les normes évoquées plus haut). Ce temps est, certes, purement intellectuel, il n’impose qu’une chronologie, du moins en ce qui concerne l’objet. Il n’en reste pas moins que, suivant cette chronologie, les flèches à double sens sont caduques et font place à des flèches qui ne vont plus que dans un seul sens63 et qui doivent pouvoir s’enchaîner les unes aux autres. Or, la chronologie ne se substitue pas simplement à la logique hiérarchique du carré ; elle s’y ajoute. Ainsi, dans la figure 23, la détermination d’un parcours entre la confiance et la défiance n’annule pas la relation de contradiction existant entre ces termes. Le parcours s’en nourrit au contraire afin de se constituer en parcours de transformations, ce dont témoignent également les indices et les signes, plus loin les preuves, qui le jalonnent. Quant à l’enchaînement des flèches dans ce parcours, et des relations qui sont leurs objets, il ne participe pas davantage à la logique initiale du carré, et même contraint-il à reconsidérer les relations entre les relations elles-mêmes, selon les diverses possibilités d’une « chronologie ».
Fontanille & Zilberberg
- Note de bas de page 64 :
-
Ce qui ne signifie pas que Tension et Signification soit le premier essai sémiotique où il apparaît.
Le travail entrepris sur les limites de la logique graphique du carré sémiotique trouve son accomplissement dans Tension et Signification. Deux nouveaux types de graphiques y sont présentés. D’une part, un nouveau type de variante du carré sémiotique ; d’autre part, un graphique resté encore inaperçu dans notre corpus64, que l’on appellera un quadrant. Leur représentation dans l’ouvrage est massive : 20 carrés sémiotiques appartenant à la même variété, 17 quadrants, à quoi s’ajoutent 18 tableaux à quatre cases, les autres types de graphiques se produisant en nombre plus réduit (une dizaine de tableaux à plus de quatre cases et une dizaine de schémas autres que les carrés susmentionnés) ; les formules sont également nombreuses, mais très simples (elles se bornent, le plus souvent, à manifester, entre deux éléments verbaux, un symbole logique, tels une flèche d’implication, une flèche d’équivalence, ou encore un symbole d’égalité) et souvent insérées dans un paragraphe (c’est-à-dire, sans faire état d’un format spécifique).
- Note de bas de page 65 :
-
J. Fontanille & C. Zilberberg, Tension et signification, op. cit., p. 163.
La variété de carré sémiotique présente dans l’ouvrage ne donne lieu elle-même pratiquement à aucune variation. À peine peut-on observer que les termes placés aux extrémités sont quelquefois constitués, de part et d’autre de l’axe vertical, en niveau inférieur d’arbres à deux niveaux. Aussi cette variante accuse-t-elle, elle aussi, une tendance au formatage. En voici un spécimen65 :
Fig. 25 - « Procès des passions élémentaires sous-tendant les formes de vie » (Fontanille & Zilberberg, Tension et Signification)
- Note de bas de page 66 :
-
J’aurais dû parler, dans tout ce qui précède, de « ligne fléchée » au lieu de « flèche » car, je m’en avise à présent, la précision importe. Je me retiens pourtant d’amender le texte en ce sens, persuadé que le lecteur s’en sera avisé en même temps que moi.
Cette variante donne à voir un intéressant compromis graphique entre le parcours institué dans Sémiotique des passions et le carré sémiotique standard (celui que Sémiotique tient pour « définitif »). En comparaison avec la figure 23, la figure reproduite ci-dessus, d’une part, présente deux parcours au lieu d’un, d’autre part, unifie chacun de ces parcours en le présentant par une ligne fléchée unique (comportant un angle) au lieu de deux66. Elle semble de ce fait étendre et approfondir le travail graphique exercé par la figure 23 sur le carré sémiotique standard. Dans le même temps, elle se rapproche de celui-ci : elle restaure ses quatre extrémités ; de plus, elle présente tous les parcours prévus par la théorie, de sorte qu’une structure se dégage à nouveau de sa composition.
- Note de bas de page 67 :
-
Les procès seraient-ils, pour cette raison, également contradictoires ? La théorie sémiotique gagnerait à s’emparer de cette question.
Là encore, il importe de bien comprendre que c’est par l’entremise des moyens graphiques qu’est mis en avant cet aspect de l’analyse sémiotique pourvue par leur objet, aspect qui n’est nullement explicite dans le commentaire, ni d’ailleurs, me semble-t-il, parfaitement théorisé par les auteurs. En conformité avec les propositions de Greimas, Fontanille & Zilberberg affirment que le carré sémiotique, y compris la variante qu’ils en proposent, a pour objet des procès, c’est-à-dire des relations syntagmatiques établies entre des relata. Mais le carré sémiotique, en réalité, montre davantage que des relations syntagmatiques ou supposées telles ; il fait état également, par ses moyens graphiques, de corrélations paradigmatiques posées entre ces relations ainsi que de relations syntagmatiques entretenues par ces mêmes relations ; bref c’est bien une structure de procès qu’il fait voir. L’analyse paradigmatique de la variante du carré actuellement en examen dégage, primo, que le paradigme des procès compte deux membres et, secundo, eu égard à la symétrie (sur l’axe vertical) de leur présentation graphique, que ces procès sont des contraires. L’analyse syntagmatique ajoute que ces procès ont deux relata en commun et qu’en outre, eu égard à leur croisement graphique, ils inversent la chronologie de ces relata communs67. Des tests graphiques permettent de démontrer, si nécessaire, que ces propriétés sont bien distinctes les unes des autres :
Fig. 26 et 27 - Tests pour l’analyse de la fig. 25
La figure 26 correspond à l’analyse paradigmatique de la figure 25 sans rien avoir en commun avec son analyse syntagmatique. La figure 27 partage avec la figure 25 l’analyse paradigmatique et une partie, mais une partie seulement, de l’analyse syntagmatique. Une adéquation structurelle relie donc le carré — à tout le moins le parallélogramme reconnu pour être une manifestation du format graphique appelé « carré sémiotique » — à son objet : seul un carré est capable de faire voir les propriétés paradigmatiques et syntagmatiques qui structurent son objet. À cet égard, malgré le franchissement d’une limite théorique due à l’introduction d’un facteur temporel absent du carré sémiotique standard, la variante qui vient d’être examinée est en tous points conforme à la pensée graphique initialement mise en œuvre dans le carré de Greimas & Rastier (Fig. 14).
- Note de bas de page 68 :
-
J. Fontanille & C. Zilberberg, Tension et signification, op. cit., p. 96.
- Note de bas de page 69 :
-
Ibid.
La conformité graphique de la variante au carré standard n’implique pas cependant que l’objet de cette variante soit automatiquement conforme à l’objet du carré sémiotique. Autrement dit, rien ne permet de dire que la structure dégagée par la variante soit une structure élémentaire du sens telle qu’a permis de la théoriser le carré sémiotique. Dans le cas examiné, il s’avère qu’elle ne l’est pas. Les auteurs assument cette non-coïncidence, eux qui reconnaissent (à propos d’une figure que notre figure 25 reproduit à travers les termes verbaux qu’elle met en italique) que le carré est « homogène mais non canonique »68. Nous pouvons raisonnablement mettre sur le compte de l’adéquation graphique la propriété d’ « homogénéité » reconnue par les auteurs à leur variante au regard du carré sémiotique standard, propriété qui, d’après ce qui vient d’être développé plus haut, se vérifie pour n’importe quelle variante. Resterait à déterminer — ce que les auteurs ne prennent pas la peine de faire de manière explicite — en quoi ladite variante peut être ou non « canonique ». Il faut, pour saisir l’enjeu de cette détermination, se référer à un tableau qui, dans Tension et Signification, est présenté juste avant la figure du carré « non canonique »69 :
|
Visée tonique |
Visée atone |
|
|
Saisie tonique |
Plénitude |
Inanité |
|
Saisie atone |
Manque |
Vacuité |
Fig. 28 - Réseau des relations entre sujet et objet tensifs (Fontanille & Zilberberg, Tension et Signification)
Pour que la structure présentée dans le tableau concorde avec celle présentée dans la figure 25, il faut, premièrement, que le tableau dispose en colonnes des contradictoires (Plénitude ≅  ; Manque ≅
; Manque ≅ 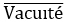 ) et en lignes des contraires (Plénitude ≅ non-Manque ; Inanité ≅ non-Vacuité) et, secondement, que le carré puisse disposer ses termes et ses relations, comparativement à la figure standard, en fonction d’un retournement symétrique sur l’axe diagonal s1 –
) et en lignes des contraires (Plénitude ≅ non-Manque ; Inanité ≅ non-Vacuité) et, secondement, que le carré puisse disposer ses termes et ses relations, comparativement à la figure standard, en fonction d’un retournement symétrique sur l’axe diagonal s1 – 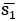 . A priori, aucune de ces opérations n’est illégitime. Les tableaux et les carrés sémiotiques, tout de même que les arbres et les formules d’homologation, sont des formats qui peuvent subir des transformations symétriques en fonction de n’importe quel axe orthogonal ou diagonal sans que la structure de leurs objets en soit affectée. Simplement, au lieu de lire les relations d’implication de bas en haut, comme on a l’habitude de le faire, il faudrait dans la figure 25 les lire de la droite vers la gauche. Les procès qu’elles présentent iraient en ce cas d’un terme à son contradictoire puis au contraire (ou, le cas échéant, au subcontraire) de ce contradictoire.
. A priori, aucune de ces opérations n’est illégitime. Les tableaux et les carrés sémiotiques, tout de même que les arbres et les formules d’homologation, sont des formats qui peuvent subir des transformations symétriques en fonction de n’importe quel axe orthogonal ou diagonal sans que la structure de leurs objets en soit affectée. Simplement, au lieu de lire les relations d’implication de bas en haut, comme on a l’habitude de le faire, il faudrait dans la figure 25 les lire de la droite vers la gauche. Les procès qu’elles présentent iraient en ce cas d’un terme à son contradictoire puis au contraire (ou, le cas échéant, au subcontraire) de ce contradictoire.
Fig. 29 - Interprétation de l’objet de fig. 25 en concordance avec l’objet de fig. 28
Il est douteux que cette interprétation rencontre les intentions des auteurs. Rien en effet ne permet de supposer que ceux-ci fassent jamais recours aux propriétés de symétrie des graphiques qu’ils utilisent. Pour cette raison, on ne pourra pas déterminer avec certitude ce qu’ils entendent par carré « non canonique » : il se peut que la propriété du « non canonique » renvoie aux possibilités de transformation symétrique du carré ; une hypothèse plus plausible serait cependant que le carré présenté dans la figure 25 corresponde bien à la disposition du carré standard, en dépit de la contradiction, alors inévitable, qu’expose la confrontation de cette figure avec le tableau de la figure 28. En revanche, il me semble qu’on entrevoit quel enjeu la difficulté soulevée peut avoir pour la pensée graphique mise en œuvre en sémiotique, et pour la pensée sémiotique elle-même.
Jusqu’à présent, ce que l’examen des graphiques sémiotiques a pu mettre en avant, à titre de caractère sémiotique de leurs objets, c’est la structure de ces objets. Et qu’est-ce qu’une structure dans une présentation graphique ? Grosso modo, on l’a caractérisée comme une organisation de relations entre relata. Une structure ainsi conçue est mise en avant, avec plus ou moins de succès, par chacun des formats que nous avons examinés : le schéma arborescent de Hjelmslev (fig. 2), le schéma à trois cases du même (fig. 4), la formule d’homologation de Greimas (fig. 7), le carré sémiotique de Greimas & Rastier (fig. 14) et la variante « processuelle » de ce carré par Fontanille & Zilberberg (fig. 25). Si les graphiques ont participé à l’élaboration de la théorique sémiotique, c’est précisément parce qu’ils entrent pour une part dans la conceptualisation de leurs objets. Certes, leurs moyens spécifiques ne permettent pas de présenter l’ensemble des caractéristiques qui les définissent. En revanche, ce qu’ils en présentent, ils le font voir au sein d’un jeu de possibilités et d’impossibilités qui, à chaque fois, a coïncidé avec les propriétés des formats utilisés. En ce sens, les formats graphiques et formulaires ont bel et bien contribué à la transformation des relations structurelles (depuis la dichotomie jusqu’au procès, en passant par l’homologation, la tripartition de la contradiction, de la contrariété et de l’implication, et la détermination syntagmatique ou paradigmatique sous-jacente à toutes ces relations) parce qu’ils ont présenté la structure elle-même sous des jours différents.
J’appellerai « principe structural » le mouvement selon lequel la sémiotique poursuit son évolution théorique en fonction d’une réflexion s’articulant autour de la notion de structure. J’affirme alors que le problème soulevé par l’orientation du carré dans la figure 25 ne relève plus, quant à lui, de ce principe structural mais de ce que je propose d’appeler un « principe figural », et je laisse entendre — il faudrait un cadre plus large que celui d’une étude sur les graphiques sémiotiques pour être plus affirmatif à ce sujet — que son enjeu est de provoquer un infléchissement dans l’évolution de la réflexion sémiotique.
Est-ce seulement par convention que les lignes fléchées sont orientées comme elles le sont dans la figure 25 ? En tout cas, il n’y aurait rien dans la structure de l’objet qui les empêcheraient d’être orientées différemment :
Fig. 30-32 - Changements d’orientation de la fig. 25
Les rapports syntagmatiques et paradigmatiques qui déterminent la présentation graphique de cette structure sont intégralement conservés dans les trois figures ci-dessus. Supposons alors, pour commencer, qu’il s’agisse bien d’une convention, et reconnaissons-en les effets. Le carré subit un figement permettant de ne pas préciser les différents types de relations qui définissent sa structure, ce qui conduit progressivement à laisser ces relations dans un état d’indifférenciation. C’est cette indifférenciation que nous voyons à l’œuvre dans la figure 25, puisque, d’une part, chaque relation établie entre les lignes et les colonnes du tableau à quatre entrées de la figure est interprétable, selon le besoin du carré à construire, soit comme une relation de contrariété soit comme une relation de contradiction, et que, d’autre part, la relation d’implication telle qu’elle est apparaît dans le carré sémiotique standard n’y est pas strictement présentée (c’est-à-dire qu’ou bien elle l’est de façon « non canonique », ou bien elle ne l’est pas du tout). De ce fait, le carré trouve dans cette variante particulière un format graphique nouveau, ou du moins la visée d’un formatage distinct du sien : un format qui ne serait plus, entre autres propriétés, symétrique. Ainsi le figement graphique de la variante tient-il lieu de détermination structurelle. En même temps il permet l’émergence d’un autre type de relations dans le carré : des relations chronologiques.
Risquons-nous à présent à aller au-delà de ce que permet de dire l’aspect conventionnel de la présentation graphique, et supposons que la variante présente quelque chose de son objet qui ne serait pas présent dans le carré sémiotique standard. La supposition semble raisonnable dès que nous admettons de reporter sur elle ce qui avait été dit de la figure 23 (où un seul parcours était présenté). Ce qui apparaît alors, ce sont des figures du sens. J’en présenterai trois :
-
la pliure : le sens paraît devoir toujours être plié, dévié, voire brisé ; la relation sémantique aurait trois endroits remarquables : son point de départ, son point d’arrivée et le point où elle se plie, ces trois points correspondant chacun à la possibilité d’une désignation terminologique ;
-
le croisement : le sens aurait toujours à choisir entre deux parcours possibles et se situerait à la croisée de ces parcours, c’est-à-dire au centre de quatre vecteurs sémantiques qu’opposent deux à deux l’origine et la finalité ;
-
enfin, en tenant compte à la fois de l’orientation des parcours et de la valeur chronologique qui leur est attribuée, il est possible de concevoir le sens comme une pente douce suivie d’une brutale remontée ; le sens serait donc également affaire de changements de vitesse, de décélération et d’accélération, ou de progression et de saut, figure qui fait voir le sens comme une pulsation.
Il n’y a pas à rendre légitimes de telles figures que nul, peut-être, ne songerait à défendre. Il suffit que l’on puisse les voir dans le graphique pour que se pose la question de savoir si le graphique lui-même les fait voir, autrement dit la question de savoir si ces figures peuvent être des éléments de contenu de la sémiotique graphique. Auparavant, nous nous étions tenus à ce qui avait paru nécessaire à l’adéquation du graphique à son objet, à savoir la structure. Puis nous avons dû convenir de la présence d’une convention plus remarquable que d’autres, dont l’effet le plus apparent consistait dans le figement des figures en direction d’un possible formatage. Nous sommes à présent confrontés à la question de savoir si les figures qui apparaissent à la suite de ce figement conventionnel relèvent du pur accident, de la contingence, ou si nous sommes en droit au contraire de leur attribuer une signification selon laquelle ces figures seraient à même de figurer le sens. D’autres présentations graphiques, en employant d’autres moyens, les auraient fait disparaître : la troisième figure mentionnée ne résiste pas aux changements d’orientation des lignes fléchées des Fig. 30-32 ; la seconde, aux tests effectués aux Fig. 26 & 27 ; la première est mise à mal par les Fig. 24 & 28. Ce qui m’incline à tenir pour raisonnable la question portant sur la valeur de leur présence dans les graphiques est que ces figures n’expriment pas la structure de l’objet mais qu’elles n’y contreviennent pas non plus et que, par ailleurs, elles entrent en adéquation avec le fondement chronologique du sens. Je définirai alors le principe figural comme le mouvement selon lequel un objet abstrait, soit pur concept soit pure matière, est appelé à être saisi par une figure.
Remarque : Je réserve pour plus tard le devoir de préciser ce que j’entends par « figure », mais il me semble utile de m’arrêter dès à présent sur l’ambivalence qui est concédée ici à ce mot. Il paraît en effet que le mot « figure » est pris selon deux acceptions : l’une en fait la manifestation de certains formats, dont les graphiques et les formules, mais aussi les dessins et les photographies, et en somme de tout ce qui a trait aux images ; l’autre le lie au principe figural. Je ne pense pas avoir suscité artificiellement leur rencontre, car ces acceptions sont fondées soit par l’usage soit par la dérivation morphologique. Mais je veux faire aussi remarquer que cette rencontre n’est pas fortuite. Une figure, au sein d’un texte, désigne ce qui est figuratif dans l’espace de ses pages, mais aussi ce qui pourrait être considéré conceptuellement comme tel. L’ambivalence du mot « figure » n’est du reste pas très éloignée de celle qui est assumée par le mot « sens » en raison de la présence de ses acceptions « spatiale » et conceptuelle.
Au reste, ce qui pourrait être apparu comme une spéculation un peu vaine va, je l’espère, rencontrer davantage d’adhésion avec l’examen du dernier type de graphique compris dans notre corpus, le quadrant. Les spécimens que j’ai choisi de présenter entrent en correspondance avec la variante « figurale » du carré sémiotique reproduite dans la figure 25. Ils sont d’ailleurs présentés côte à côte dans Tension et Signification sur la même page que cette figure et la correspondance est explicitement établie par les auteurs :
- Note de bas de page 70 :
-
Ibid., p. 163.
Nous avons jusqu’ici considéré le système des passions élémentaires sous-tendant les formes de vie. Abordons maintenant ces mêmes passions du point de vue des procès70.
L’argument de la présente étude a requis que nous suivions un ordre de présentation inverse à celui choisi par les auteurs. Voici donc à présent les graphiques « représentant » (their word) le système :
- Note de bas de page 71 :
-
Ibid. La reproduction des figures s’est efforcée d’être scrupuleuse. J’y ai cependant apporté volontairement une modification parce qu’elle m’a parue devoir entrer, en fonction d’autres graphiques du même type présents dans l’ouvrage, dans les intentions des auteurs : dans Fig. 34, la courbe a été tracée en gras.
Fig. 33 & 34 - « Système des passions élémentaires » (Fontanille & Zilberberg, Tension et Signification)71
J’aurai à commenter dans la section suivante le format du quadrant. Je me contenterai, avant de clore celle-ci, de chercher à cerner la forme d’adéquation que ces figures entretiennent avec leur objet puis d’interroger leur correspondance avec la figure 25.
On commencera par constater la présence de termes contradictoires, tonique vs atone, répartis aux extrémités de chaque axe. Les axes exprimant par leur orthogonalité une certaine opposition, il est également licite de considérer que saisie et visée entrent dans une relation de contrariété. La possibilité de leur opposition se voit confirmée par le tableau reproduit en Fig. 28. La présence de telles relations suffit dès lors à faire l’hypothèse d’un carré sémiotique sous-jacent au graphique :
Fig. 35 - Microsystème sémantique de la perception
En conséquence, on doit convenir que dans le quadrant ce carré a été transposé en une présentation orthogonale. Cependant, ainsi qu’il en est dans la figure 28, saisie et visée ne composent un système que dans le but de servir de paramètres pour de nouvelles oppositions, celle de l’ennui et du bonheur dans la figure 33, celle de la nostalgie et de l’attente dans la figure 34. Or il est patent que les deux figures, pourvu qu’elles correspondent bien au format du quadrant, peuvent être superposées, car leurs axes sont déterminés de façon identique. Ce qui apparaît alors, c’est à nouveau une figure de carré sémiotique. La figure 25 montre du reste que les éléments verbaux de ces oppositions entrent effectivement dans un carré sémiotique. Aussi apparaît-il comme plausible que le quadrant ait pour fonction, en sémiotique, de présenter deux microsystèmes sémiotiques hiérarchisés, dont deux carrés sémiotiques pourraient rendre compte.
Il apparaît cependant que le carré ainsi composé par la superposition des deux quadrants ne correspond pas au carré élaboré avec les mêmes termes que montre la figure 25. Assumerait-on d’y exercer les transformations de symétrie d’application dans les carrés standard que leur concordance n’aboutirait pas mieux. Deux hypothèses concurrentes se présentent pour expliquer cette non-concordance. L’une a un air de plausibilité qui la fait avancer en premier : comme le carré sous-jacent est transposé en axes orthogonaux, il semble juste que les relations du carré hiérarchiquement inférieur soient disposées dans le quadrant autrement qu’elles ne le sont dans le carré standard. Si le point (+, +), ayant en abscisse et en ordonnée la valeur +, correspond à s1, 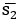 correspondra nécessairement au point (–, –), c’est-à-dire que la relation d’implication entre s1 et s2 sera posée sur un axe diagonal. Suivant ce raisonnement, BONHEUR devrait être en relation d’implication avec ENNUI. Cela est infirmé par le carré de la figure 25 : si Bonheur correspond en effet à s1, par contre c’est Attente qui se trouve en
correspondra nécessairement au point (–, –), c’est-à-dire que la relation d’implication entre s1 et s2 sera posée sur un axe diagonal. Suivant ce raisonnement, BONHEUR devrait être en relation d’implication avec ENNUI. Cela est infirmé par le carré de la figure 25 : si Bonheur correspond en effet à s1, par contre c’est Attente qui se trouve en 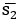 . L’hypothèse ne se vérifie donc pas. Parions alors sur la seconde hypothèse, qui consiste à admettre avec les auteurs que, selon la nature de son objet, système ou procès, un carré sémiotique est susceptible de présenter des dispositions distinctes des termes qui composent cet objet. Hypothèse décevante, car le commentaire accompagnant les graphiques ne justifient pas cette disparité, laquelle demeure ainsi inaccessible au raisonnement graphique.
. L’hypothèse ne se vérifie donc pas. Parions alors sur la seconde hypothèse, qui consiste à admettre avec les auteurs que, selon la nature de son objet, système ou procès, un carré sémiotique est susceptible de présenter des dispositions distinctes des termes qui composent cet objet. Hypothèse décevante, car le commentaire accompagnant les graphiques ne justifient pas cette disparité, laquelle demeure ainsi inaccessible au raisonnement graphique.
Entre la variante figurale du carré et les quadrants, il existe une autre disparité, elle entièrement graphique, et éclatante. C’est que la figure 25 présente des procès, alors que les quadrants pris ensemble ne présentent à eux deux qu’un système. Que les quadrants doivent être considérés comme deux figures distinctes n’est guère contestable : d’autres quadrants présents dans l’ouvrage fonctionnent en solo. À quoi est dû alors que la présentation du système soit scindée en deux graphiques ? Là aussi, on pourrait admettre un motif conventionnel : étant donné que les quadrants sont superposables (un quadrant unique aurait pu s’y substituer), il sera seulement apparu aux auteurs que la dissociation en deux quadrants rende plus lisibles les relations du système. Mais s’agit-il seulement d’une convention ? C’est ce qu’il n’est pas possible, cette fois, de soutenir, car le conventionnel a outrepassé ici sa limite : les graphiques ne font plus voir la structure du système, dès lors qu’ils désarticulent ce dernier en deux composantes.
Que font-ils voir alors ? Des figures : en l’occurrence, des courbes – et des courbes reconnaissables, identifiables, selon d’autres discours (celui des mathématiques et de leurs applications), comme des paraboles et des hyperboles — je reviendrai sur cette identification. Intéressons-nous pour le moment aux valeurs que prête la courbe graphique à son objet. Le sens ne contient plus de pliure, ni de rencontre en son croisement, mais il est assurément encore un parcours, un parcours ascendant ou descendant. La chronologie elle-même est mise en suspens, car il n’y a pas de flèches sur ce parcours ; il n’y a pas dès lors à associer nécessairement telle courbe, mettons celle de la figure 33, avec un parcours particulier, par exemple l’ascendant. La courbe toutefois est sous-tendue par une dynamique de lignes fléchées orthogonales et non enchaînables. C’est pourquoi il est permis de considérer que la courbe est mise « sous tension » : le parcours peut se prolonger, au-delà de la présentation graphique qui en est faite, dans les deux sens. « Tension du sens entre deux sens » : saluons le retour d’une ambivalence lexicale dans l’enjeu de cette nouvelle présentation graphique.
Zilberberg
De la même manière que le carré a pu subir une série de modifications, les unes visant la simplification les autres (quelquefois de concert avec les premières) l’hybridité avec d’autres graphiques, le quadrant va pouvoir être ramené, dans les Éléments de grammaire tensive, à ses éléments essentiels, ou au contraire recevoir de nouvelles déterminations. Les éléments essentiels sont au nombre de trois : les axes orthogonaux, les courbes et les coordonnées.
- Note de bas de page 72 :
-
Cf. Claude Zilberberg, Éléments de grammaire tensive, Limoges, pulim 2006, pp. 207-210.
Les axes constituent la composante inchangée à chaque manifestation graphique. Les objets qu’ils présentent connaissent d’ailleurs la même constance : l’axe vertical correspond toujours à un axe sémantique d’intensité, l’axe horizontal, à un axe d’extensité. Certes, il n’est pas toujours évident de rapporter les déterminations particulières de ces axes, comme elles sont présentées dans les graphiques, selon l’opposition première de l’intensité et de l’extensité ; mais nulle part non plus on ne trouve d’indication explicite contraire à la possibilité de ce report. Pour revenir au langage graphique, on remarquera que ces axes forment un seul angle droit. Jamais il n’est envisagé qu’ils puissent être prolongés de manière à former d’autres quadrants. Si le graphique a une allure diagrammatique, il se distingue par conséquent des diagrammes utilisés dans d’autres discours (en particulier dans le discours des mathématiques) par cette caractéristique que toutes ses données sont contenues dans un seul quadrant. Pour cette raison, je préfère m’en tenir à la désignation de quadrant tensif, bien que Zilberberg présente généralement de tels graphiques au moyen du terme de diagramme72.
Les courbes présentent également un aspect très régulier : il n’y en a que de deux sortes. Elles ont un air de parabole ou d’hyperbole — mais un air seulement. Du fait de la présence d’un quadrant unique, elles ne présentent jamais qu’une moitié de parabole ou d’hyperbole. En outre, pour les désigner de cette façon, il faudrait admettre que leur détermination en tant que telle soit liée à leur présentation graphique, ce qui n’est pas le cas en mathématiques (il existe des hyperboles qui présentent une tout autre orientation par rapport aux axes orthogonaux). D’ailleurs, je ne crois pas que Zilberberg se risque jamais à de telles désignations.
- Note de bas de page 73 :
-
Ibid., p. 208.
À l’entrée « Diagramme » du glossaire, les courbes sont présentées dans des graphiques métasémiotiques sous les désignations de corrélation inverse et de corrélation converse73.
Fig. 36 & 37 - Corrélation inverse et corrélation converse (Zilberberg Éléments de grammaire tensive)
De telles désignations, inverse et converse, impliquent que les valeurs attribuées aux axes le soient de manière homogène, conformément aux déterminations diagrammatiques dans les mathématiques. Autrement dit, une présentation graphique qui inverserait, eu égard au sens des flèches, l’ordre des valeurs n’est jamais envisagée pour les quadrants tensifs :
Fig. 38 - Ceci n’est pas un quadrant tensif (test d’homogénéité des valeurs)
Pour autant il n’est pas possible de confondre le quadrant tensif avec le quadrant des positivités, tel qu’il est en usage dans les mathématiques : au contraire de ce dernier, le graphique sémiotique semble pouvoir réunir dans un seul quadrant les valeurs positives et les valeurs négatives de chacun de ses axes. Ceci sera examiné plus en détail avec la considération du troisième élément essentiel des quadrants tensifs, à savoir les coordonnées.
- Note de bas de page 74 :
-
Ibid., p. 152.
Voyons auparavant ce qu’on peut dire encore sur les courbes. Il avait été noté, à la fin de la précédente section, que les courbes (au contraire des axes) n’avaient pas de sens, et ne présentaient de ce fait aucune chronologie. Ce n’est pas tout à fait exact. Lorsque les quadrants contiennent des points associés à des symboles numériques, ces symboles sont toujours ordonnés en ordre ascendant de la gauche vers la droite. Néanmoins, le parcours qui consiste à lire la courbe de la droite vers la gauche reste possible. Ceci permet de considérer qu’il existe pour chaque courbe un parcours plus « facile » ou plus « naturel » que l’autre (la pertinence de telle ou telle qualification du parcours dépendant du sémantisme de son objet), allant de gauche à droite, et un autre plus « difficile » ou plus « exceptionnel », allant de droite à gauche. Pour une corrélation inverse, le parcours descendant semble ainsi plus naturelle que l’ascendant qui, pour cette raison, sera considéré comme une « remontée », ainsi que l’illustre le graphique suivant74 :
Fig. 39 - Le survenir (Zilberberg, Éléments de grammaire tensive)
- Note de bas de page 75 :
-
Ibid., p. 206.
Pour une corrélation converse, c’est au contraire le parcours ascendant qui se lit par défaut, le parcours descendant pouvant être perçu comme une « régression » ou comme un « recul ». Par ailleurs, les deux courbes elles-mêmes ne sont pas sur une balance en nombre égal. Les quadrants contenant une corrélation inverse sont beaucoup plus nombreux que les quadrants à corrélation converse, disproportion remarquée et assumée par l’auteur sur le plan théorique : « Dans les analyses concrètes, la décadence prévaut largement »75.
Cette dernière citation permet d’observer que la sémantisation différenciative des parcours exprimés par les courbes graphiques entre en adéquation quasi complète (et instantanée) avec la conceptualisation théorique élaborée par Zilberberg entre implication (la règle, le régulier) et la concession (qui fait événement). Il est même délicat de distinguer ici la sémantique graphique et la sémantique des concepts sémiotiques, tant les termes de ceux-ci semblent rendre compte, voire être redevables, de leur visualisation graphique. Je me suis permis de parler, en ce qui concerne la visualisation graphique, de « parcours descendant », au lieu de « décadence », terme qui, me semble-t-il, appelle une justification absente des graphiques ; mais chacun admettra, je suppose, que « descendance » et « décadence » ont un sème spécifique en commun. À cette nuance près, les courbes persévèrent donc, à travers les déterminations susceptibles de les affecter, à faire voir quelque chose de l’analyse sémiotique (qui est leur objet) ainsi qu’elle est théorisée dans les Éléments de grammaire tensive. Or le « quelque chose » qu’elles font voir n’appartient pas au registre de la structure. Cela tient à un aspect de la syntagmatique, plus exactement au parcours sémantique que le sujet producteur ou interprète accomplit dans une syntagmatique. La présentation graphique de ce parcours, ai-je prétendu, relève d’un principe figural. Ceci acquiert à présent une sorte d’évidence : le concept sémiotique d’ascendance est bien présenté par une figure ascendante, celui de décadence par une figure descendante. La norme de lecture, qui conduit à lire les courbes graphiques de la gauche vers la droite, non seulement permet leur distinction, mais suscite en outre la possibilité de lectures plus difficiles et plus rares, des « remontées » et des « régressions » ou « reculs ».
Il est temps d’en venir à ce qu’annonçait la remarque que j’ai été amené à faire concernant les figures et leur ambivalence. Les figures qui manifestent des graphiques, des dessins, des images ne se manifestent pas n’importe où n’importe comment ; ordinairement, elles sont reproduites dans un livre. Qu’est-ce à dire ? D’une part, que les figures voisinent avec des manifestations textuelles (verbales). Dans le livre, on a ainsi à distinguer des éléments textuels non figuratifs et des éléments figuratifs. Il en est de même selon d’autres médias, tels la projection PowerPoint ou l’affichage numérique, où l’utilisation du terme de figure dans cette acception ne semblerait pas déplacé. D’autre part, cela signifie que les figures sont soumises à des protocoles médiatiques de reproduction présupposant un original. Une figure reçoit à ce titre davantage de caractérisation que le concept hjelmslevien de manifestation, dont elle est néanmoins une application. L’original de la figure n’est pas seulement pour elle une forme ; il est pour elle un modèle, empiriquement antérieur, de ressemblance. Ce qui est pris en compte dans la figure, quel que soit le mode de reproduction (et les transformations inhérentes à ce mode) et quelle que soit la nature de l’original (graphique, dessin, photographie…), ce sont des traits de figurativité à travers lesquels on considère que la figure reproduit l’original. C’est par là aussi que je définirai la figure quand elle découle d’un principe figural. Une figure, dans l’un ou l’autre de ses usages (soit en tant que concept soit en tant que manifestation), correspond simplement à ce qui est tenu pour figuratif, par opposition au non figuratif (le textuel, l’abstrait). Et le principe figural trouve alors à se redéfinir, non moins simplement, comme le mouvement par lequel un objet abstrait devient un objet figuratif à travers la figure qui le saisit.
- Note de bas de page 76 :
-
Voir S. Badir, « À quoi servent les graphiques », art. cit.
Quand il est soumis au principe figural, le graphique invente pour son objet une substance phénoménologique dont il présente l’analyse. Le graphique sémiotique retrouve par là la fonction première de tout graphique qui est d’accomplir une analyse phénoménologique de son objet76. L’infléchissement que le principe figural exerce sur la pensée sémiotique, si toutefois on admet d’en faire l’hypothèse, correspond ainsi à une meilleure adéquation de l’instrument graphique à l’égard la théorie, bien à même de valoriser sa modalité épisémiotique, et n’est pas non plus étranger à la réflexion sémiotique qui peut être portée sur ces graphiques, comme son faire autocritique l’y engage.
- Note de bas de page 77 :
-
Louis Hébert, « Le schéma tensif » Signo [en ligne], 2005, http://www.uqar.qc.ca/signo/fontanille/tensif.asp.
Une structure n’avait pas à être figurative. C’est pourquoi sa présentation graphique pouvait connaître des transpositions. Le principe figural implique en revanche que chaque présentation graphique avance une figure de son objet. Il existe certainement une possibilité de variabilité des figures, eu égard à leur statut de manifestations, mais la limite en est tracée par un critère de ressemblance. Ainsi, par exemple, lorsque Louis Hébert, présentant le « schéma tensif » de Fontanille & Zilberberg, donne pour figure de corrélation directe (sic) le schéma suivant77 :
Fig. 40 - « Exemple de corrélation directe » (Hébert, « Le schéma tensif »)
- Note de bas de page 78 :
-
Présenté dans J. Fontanille & C. Zilberberg, Tension et Signification, op. cit.,, p. 19.
il n’est pas sûr qu’il rencontre les intentions des auteurs. La transformation qu’il impose à la présentation de la corrélation, qui de courbe devient droite, interdit en tout cas certainement de tenir sa figure pour identique à la figure du quadrant original78. De manière analogue, on serait en droit d’interroger la théorie de la sémiotique tensive en apportant à la corrélation converse la transformation suivante, jamais envisagée par Zilberberg :
Fig. 41 - Alternative pour la corrélation converse
Les différences de signification entre le quadrant original et les deux quadrants des fig. 40 et 41 sont immédiatement perceptibles : elles concernent la possibilité d’atteindre une limite indépassable dans les valeurs accordées à l’un ou l’autre des axes tensifs. Il me paraît évident que ces différences mériteraient d’être considérée par la théorie sémiotique. De ce que les graphiques présentent des figures, il ne s’ensuit pas qu’ils ne soient plus en mesure d’interroger leur objet, à savoir, rappelons-le une fois encore, l’analyse du sens.
- Note de bas de page 79 :
-
C. Zilberberg, Éléments de grammaire tensive, op. cit., p. 194.
La possibilité de transformation des courbes est néanmoins envisagée au moins une fois par Zilberberg dans un quadrant qui compte aussi trois axes79 :
Fig. 42 - Analyse d’une lecture de Schopenhauer par Nietzsche (Zilberberg, Éléments de grammaire tensive)
On ne saurait considérer que cette figure est la superposition de deux quadrants, comme nous avons envisagé de le faire pour Fig. 33 & 34, car ce qui importe de visualiser dans ce graphique ce sont justement des différences de courbure entre les courbes, ce que deux graphiques isolés ne feraient pas apparaître nettement. Or les courbures de courbes sont réellement prises en charge dans l’analyse de l’objet, étant donné qu’elles sont paramétrées par des valeurs distinctes sur l’axe de l’intensité ; qui plus est, les différences qu’elles font voir sont reprises dans la grammaire tensive par la théorie des intervalles. Ce qu’il faut reconnaître alors, par cette preuve supplémentaire, c’est que les figures de courbes ne sont nullement conventionnelles, elles n’expriment pas seulement une relation structurelle entre deux valeurs, mais font voir par leurs traits de figuration (ici, par le degré de déclivité) quelque chose de l’analyse du sens. Les transformations tentées dans Fig. 40 & 41 expriment à ce titre une pensée graphique participant de plein droit à la théorisation de l’objet. Il est évident que les courbes sémiotiques, en l’absence de toute coordonnée nombrable, ne pourraient pas être rapportées aux fonctions qui les génèrent en mathématiques, mais il n’est pas moins légitime de se demander quelles différences de valeurs sémiotiques produisent les figures de courbes connues en mathématiques pour des demi-paraboles, et aisément identifiables en tant que telles, selon les fonctions carré (à laquelle s’apparente Fig. 37), cubique, ou racine carrée (Fig. 41).
- Note de bas de page 80 :
-
Une interrogation de cet ordre a été menée par François Rastier à propos de la figure circulaire du signe laquelle, chez Saussure, « s’aplatit » en ellipse, laissant « présage[r] peut-être son ouverture vers les signes voisins » (François Rastier, « Le silence de Saussure ou l’ontologie refusée », Saussure, cahier dir. par Simon Bouquet, L’Herne 2003, p. 30).
C’est dans le même ordre d’idées qu’il y aurait lieu de prendre en considération l’aspect rectangulaire du carré sémiotique. Tant que celui-ci est conduit par un principe structural, la forme géométrique qui le fait voir importe peu, pourvu qu’elle soit un parallélogramme. Mais s’il venait à être repris par un principe figural, alors il importerait de se demander, en fonction des différences d’intervalles perçues entre les termes, quelles valeurs peuvent se dégager, pour le microsystème sémantique lui-même, soit d’un carré soit d’un rectangle, ou de toute autre forme qui conserve intacte sa structure80.
Un mot encore sur les figures. Les graphiques ne semblent pas les présenter exactement de la même manière que les structures. Les graphiques « contiennent » les figures : les courbes se tiennent entre deux axes ; les parcours dans la variante figurale du carré sémiotique sont balisés par des termes. Par contre, les graphiques sont constitutifs des structures qu’ils présentent, de sorte, par exemple, que dans Fig. 19 nous avons été amenés à considérer la conjonction de deux formats graphiques, le carré sémiotique proprement dit et quatre exemplaires de l’arbre, au lieu de considérer un nouveau format graphique, spécial ou complexe. Bien que le corpus réuni à l’occasion de cette étude soit trop mince pour tirer des conclusions définitives, il est à parier que cette différence de comportement soit grosse de sens. Quand le graphique exprime une structure, tout ce qui ne relève pas de la constitution de cette structure demeure conventionnel, insignifiant. Au contraire, dans un graphique conduit par un principe figural, chaque élément est amené à faire sens, les composantes variables des figures comme les éléments appartenant au format graphique. Bref, la modalité épisémiotique joue à plein rendement quand les graphiques sont gouvernés par un principe figural : le graphique vibre de ses potentialités et des hypothèses conceptuelles qu’adresse chacun de ses éléments à la réflexion sémiotique.
- Note de bas de page 81 :
-
C. Zilberberg, Éléments de grammaire tensive, op. cit., pp. 73-74.
J’aborde à présent, brièvement, la troisième composante essentielle du quadrant tensif : ses coordonnées, par quoi j’entends les valeurs qui paramètrent tant les axes que les « points » (en fait : des symboles alphabétiques ou des expressions verbales) repérés ou simplement disposés dans le quadrant. D’abord, on peut remarquer que cette composante n’est pas présente dans chaque figure de quadrant, le quadrant tensif connaissant des figures simplifiées. Pour autant, on ne doit pas tenir les coordonnées pour inessentielles, car elles sont nécessaires à l’intelligibilité de tout quadrant, quel qu’il soit, ainsi que le prouve a contrario la Fig. 38. Ceci dit, il existe une grande latitude dans le choix de ces valeurs. La tension qu’elles expriment peut être de type numérique (0 ↔ 1), algébrique (1 ↔ n + 1 ; 1 ↔ n > 1), symbolique (v1 ↔ v2 ; + ↔ –), verbale (faible ↔ fort ; concentré ↔ diffus). Il se peut même que le type de tension sémantique qu’elles expriment diffère pour chacun des axes. Le registre des tensions se laisse toutefois subsumer sous deux grands choix structurels : une structure oppositive, à laquelle nous a habitués le carré sémiotique, et une structure graduelle. L’opposition symbolique du + et du – a cette particularité de pouvoir être lue selon l’une et l’autre de ces structures, et cette caractéristique correspond sans doute à un aspect majeur de l’apport théorique de la grammaire tensive. Pourtant c’est la tension du 0 et du 1 qui est privilégiée dans les Éléments de grammaire tensive ; c’est qu’elle est sans doute la plus apte à répondre au souci que manifeste Zilberberg à reprendre les problèmes théoriques les plus généraux auxquels est confrontée la sémiotique depuis Hjelmslev. On se bornera ici à prendre à témoin, sans les commenter (le commentaire qu’il y aurait lieu de faire se rapporterait davantage aux analyses qu’aux graphiques), les deux quadrants tensifs suivants81 :
Fig. 43 & 44 - « Partition de l’espace systémique » selon le type de corrélation (Zilberberg, Éléments de grammaire tensive)
- Note de bas de page 82 :
-
Ibid., p.157.
Les structures graduelles offrent la possibilité de mettre en tension plus de deux points remarquables sur la courbe. Ces points peuvent être signalés simplement par des symboles alphabétiques, mais ils renvoient quelquefois directement aux objets analysés. Je me contente là aussi d’illustrer sans commenter82 :
Fig. 45 - Échelonnement des sujets argumentant sur la métaphore (Zilberberg, Éléments de grammaire tensive80)
Conclusions
-
Sémiotique des graphiques. — Cette étude a montré, sur un corpus donné, que l’analyse des graphiques correspond à une analyse sémiotique. L’analyse a permis de distinguer en effet un plan d’expression et un plan de contenu. Elle a établi des constantes formelles sur deux niveaux de pertinence : l’analyse des formants (lignes, flèches, parenthèses, axes, courbes, symboles, etc.) et l’analyse des formats (arbre, tableau, carré sémiotique, quadrant tensif…). Elle a décrit quelques-unes des caractéristiques propres aux manifestations graphiques que sont les figures. Elle a notamment permis de mettre le doigt sur le caractère hybride et polysémiotique de ces manifestations : une figure est susceptible de manifester à la fois des constantes graphiques (en particulier, différents formats) et des constantes appartenant à d’autres sémiotiques (formats formulaires, symboles divers, signes linguistiques, etc.).
-
Graphiques de sémiotique. — La dimension épisémiotique a démontré, à titre de modalité interprétative, toute son importance dans les graphiques produits dans les travaux sémiotiques. Le corpus rassemblé constitue une série laissant apparaître deux problématiques spécifiques à la présentation graphique de la théorie sémiotique. Premièrement, les graphiques sémiotiques ont cherché à exprimer la binarité inhérente à la pensée sémiotique et sont parvenus, grâce au carré sémiotique, et par une forme de redoublement, à la cerner. C’est cette forme de bouclage que les graphiques qui ont succédé au carré sémiotique canonique ont cherché à interroger et à suspendre, sans jamais l’abandonner tout à fait, comme le montre encore la tension existant entre 0 et 1 dans les valences des quadrants tensifs. Secondement et corrélativement, la conception structurale à laquelle avait abouti la réflexion sur la binarité a laissé peu à peu le champ libre pour un autre type de réflexion. L’inscription de parcours dans le carré sémiotique tout comme celle de courbes dans les quadrants tensifs fait état, dans la sémiotique des graphiques, d’une réflexion de type figural qu’un théoricien tel que Zilberberg cherche actuellement à intégrer dans la théorie sémiotique elle-même.
-
Sémiotique graphique. — Ce que cette étude vise finalement à montrer, c’est (i) qu’il existe un mode de production graphique, issue sans doute de modèles appartenant à d’autres savoirs (logique et mathématique, pour l’essentiel) mais qui est bientôt devenue propre à la sémiotique, et (ii) que cette production est bien celle d’une pensée (et non d’un simple mode d’expression), uniment graphique et sémiotique, évoluant au cours du temps. La modalité épisémiotique a pour caractéristique de ne pas être nécessairement produite volontairement par les usagers ; il s’en faut d’ailleurs beaucoup pour qu’elle soit seulement perçue. Mais, dans le cas de la sémiotique graphique telle qu’elle est pratiquée par ses théoriciens, il ne fait pas de doute que les aspects soulevés par la modalité épisémiotique sont appelés à devenir l’objet d’une réflexion métasémiotique déjà esquissée chez Hjelmslev et qui prend peu à peu de l’ampleur. La présente étude entend précisément apporter une contribution à la réflexion métasémiotique et épistémologique de la théorie sémiotique. Elle s’est toutefois efforcée, dans la mesure du possible, de ne pas dépasser une certaine limite dans l’analyse : il n’a jamais été question de se servir des graphiques pour argumenter contre la cohérence, voire contre la légitimité, des concepts sémiotiques que ceux-ci présentent. Au nom de quoi, en effet, une telle critique aurait-elle pu se faire valoir ? Il aurait fallu ou bien l’arc-bouter sur la légitimité d’une autre forme de pensée graphique (logique ou mathématique), objectif qui ne me paraît pas, en dépit de l’invitation lancée par Greimas, des plus utile ni même pertinent, ou bien l’étayer par une nouvelle théorie d’ensemble pour la sémiotique, ce qui n’était pas le propos recherché. Naturellement, les théoriciens de la sémiotique auront, quant à eux, selon les visées qui leur sont propres, tout intérêt à outrepasser cette limite.