Transitions : une série de tableaux inspirés par les mathématiques Transitions: a series of paintings inspired by mathematics

Introduction

La série Transitions comporte près de 200 œuvres peintes depuis 2017 par l’artiste Reg Alcorn. La Figure 1 montre un des tableaux de cette série.

Figure 1 : Let All Blues Rejoice, acrylique sur toile, 120 × 120 cm, Reg Alcorn (2019)

Crédits Reg Alcorn

Dans cet article, nous présentons les outils mathématiques utilisés par le peintre pour créer la structure de ses toiles et nous évoquons aussi, plus brièvement, son travail sur la couleur. Une version plus détaillée de ce travail, en particulier dans ses aspects mathématiques, a été proposée pour publication à une revue mathématique (Vinatier et Alcorn, 2023).

1. Au départ

Figure 2 : Le petit déjeuner de Poincaré, acrylique sur toile, Reg Alcorn

Crédits : IREM de Limoges

La collaboration a continué avec l’exposition Convergences : les mathématiques dans l’histoire de l’art, dans laquelle des tableaux réalisés par Reg Alcorn permettaient d’évoquer auprès de publics divers les liens entre mathématiques et histoire de l’art : les proportions (notamment le fameux nombre d’or), les pavages, la perspective, la géométrie dans l’art moderne. Puis avec la création et l’utilisation d’une Camera Obscura de grandes dimensions, grâce à l’appui de la Faculté des Sciences et Techniques de l’Université de Limoges qui a permis à deux de ses agents techniques, Jean-Marie Bonnetblanc et Bruno Demay, de concevoir, construire, déplacer et installer dans de nombreux lieux cette chambre noire, ancêtre très ancien de l’appareil photographique : placé à l’intérieur, les nombreux publics ont pu y vivre vivre des expériences sensorielles étonnantes tout en se familiarisant avec l’optique linéaire, les propriétés des symétries centrales, mais aussi le principe de la vision.

Figure 3 : Dodécaèdre étoilé (extrait d’un tableau de Reg Alcorn pour l’exposition Convergences) et vue de la technopole ESTER (Limoges) depuis la Camera Obscura de l’IREM de Limoges lors de la Fête de la Science 2017

Crédits : IREM de Limoges (tableau) et Stéphane Vinatier (photo)

Suite à ces expériences de diffusion de culture mathématique et scientifique, Reg Alcorn a été sollicité par le pôle Mathématiques, informatique, image du laboratoire XLIM pour illustrer les thèmes de travail de ses équipes de recherche, avec l’aide de l’IREM pour faire le lien entre les chercheurs et l’artiste. La Figure 4 reproduit le tableau évoquant l’optimisation.

Figure 4 : Hilbert hotel, acrylique sur toile, Reg Alcorn

Crédits : XLIM UMR 7252 CNRS – Université de Limoges

2. Ingrédients mathématiques

À la suite de nombreux artistes (Picasso, Mondrian, Kandinsky, Vasarely, Morellet... ), Reg Alcorn cherche un procédé géométrique pour structurer les toiles de sa série Transitions. Il puise dans les objets mathématiques découverts lors des travaux précédents.

2.1. La tuile de Truchet

Le Révérend Père Sébastien Truchet (1657–1729) est un savant de l’époque de Louis XIV avec de nombreuses spécialités : mathématicien, typographe, « horloger, grand spécialiste des canaux, inventeur d’innombrables machines (canons, machines à transplanter les arbres, cadrans solaires, etc.) dont les fameux tableaux mécaniques de Marly » (André, 2002). Lors de l’inspection d’un canal du côté d’Orléans, il tombe sur une réserve de carreaux de carrelage carrés de deux couleurs, blanc et noir, séparées par la diagonale (voir Figure 5).

Figure 5 : tuile de Truchet

Il se demande alors quelles figures agréables peuvent être réalisées avec ce motif et entame une étude combinatoire qui donnera lieu à un mémoire de l’académie royale des sciences (Truchet, 1704), dans lequel il énumère toutes les dispositions possibles de deux tels carreaux : chacun d’eux peut prendre 4 orientations et le second peut être placé le long de n’importe lequel des 4 côtés du premier, ce qui donne 64 dispositions à priori, ramenées à 32 si l’on ne distingue pas les 2 carreaux, puis à 10 à rotation près (reprenant ce travail dans un article de l’Encyclopédie, Diderot proposera une dernière réduction à 4 dispositions, à inversion des couleurs et retournement de la figure près). Si l’objectif de Truchet est décoratif (il propose à la fin de son mémoire de nombreux pavages réalisés à partir des dispositions qu’il a listées), la rigueur et l’originalité de son étude combinatoire ont été soulignées :

Truchet’s treatise is of considerable importance for it is in essence a graphical treatment of combinatorics, a subject that, under the influence of Pascal, Fermat and Leibniz, was at the forefront of mathematics at the time. (Smith and Boucher, 1987, p. 377)

2.2. La spirale d’Ulam

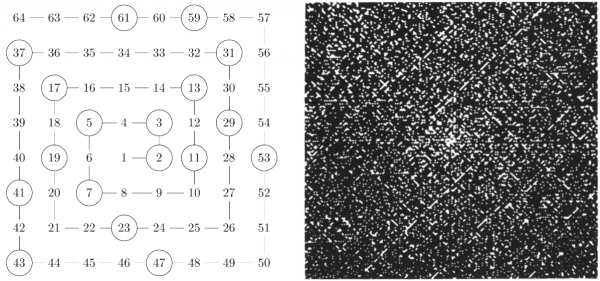
Stanislaw Ulam (1909-1984) est un mathématicien d’origine polonaise. Émigré aux USA dans les années 30, il a rejoint le projet Manhattan de fabrication de la bombe atomique à Los Alamos en 1943 et contribué de façon essentielle au développement de la bombe H. Il a également établi de nombreux théorèmes dans plusieurs domaines de mathématiques fondamentales ou appliquées. L’un de ses apports à la théorie des nombres est la spirale qui porte son nom, dont la découverte est décrite comme suit dans un article de la revue grand public Scientific American.

Last fall Stanislaw M. Ulam of the Los Alamos Scientific Laboratory, attended a scientific meeting at which he found himself listening to what he describes as a "long and very boring paper." To pass the time he doodled a grid of horizontal and vertical lines on a sheet of paper. His first impulse was to compose some chess problems, then he changed his mind and began to number the intersections, starting near the center with 1 and moving out in a counterclockwise spiral. With no special end in view, he began circling all the prime numbers. To his surprise the primes seemed to have an uncanny tendency to crowd into straight lines. (Gardner, 1964, p. 122)

Figure 6 : spirales d’Ulam 8 x 8 (nombres premiers entourés) et 255 x 255 (nombres premiers en blanc)

Crédits photo : https://www.jstor.org/stable/10.2307/24936050

Pour surprenants qu’ils puissent paraître, les alignements de nombres premiers qui apparaissent dans la spirale d’Ulam trouvent une explication dans le grand nombre de valeurs premières distinctes prises par certaines fonctions polynomiales, ainsi que l’indiquent Ulam et ses co-auteurs (Stein, Ulam and Wells, 1964). Nous y reviendrons plus loin.

3. Le procédé de Reg Alcorn

Voyons maintenant comment l’artiste utilise ces deux notions mathématiques pour créer les tableaux de sa série Transitions.

3.1. Structure

Tout d’abord, il ajoute à la tuile de Truchet dans les 4 orientations possibles un carré noir et un carré blanc :

Figure 7 : les tuiles de Truchet complétées

Il est pratique de représenter chaque tuile par une lettre, comme indiqué sur la Figure 7. Il choisit alors une séquence de ces tuiles, par exemple daadb et, plutôt que de la représenter en ligne :

Figure 8 : la séquence daadb en ligne

il l’enroule en spirale en suivant le procédé d’Ulam, autour de la première tuile de la séquence (ici d), en tournant dans le sens inverse des aiguilles d’une montre et en répétant la séquence jusqu’à remplir la surface disponible :

Figure 9 : la séquence daadb enroulée en spirale (20 répétitions)

On découvre une structure qui, bien que totalement déterminée par la séquence choisie et le procédé d’enroulement en spirale, fait apparaître des motifs en grande partie imprévisibles (la longueur de la séquence a une influence importante sur les éventuelles symétries de la structure produite). Dès qu’il obtient un ensemble de motifs qui l’inspire, l’artiste prend la main sur les mathématiques et choisit les couleurs au fur et à mesure qu’il crée le tableau.

3.2. Couleurs

Le choix des couleurs est déterminant pour le résultat final. C’est le cœur du travail de Reg Alcorn dans cette série, pour lequel il puise dans son expertise de l’utilisation de la couleur et dans sa sensibilité artistique. Nous décrivons ici simplement les grandes lignes de ce travail sur la couleur.

Pour commencer, Reg Alcorn choisit deux couleurs qui se complètent bien, par exemple un rouge et un vert (le choix des types de pigments de chaque couleur a une grande importance pour le ressenti final, même si nous n’entrons pas dans ces considérations) et il attribue l’une des deux aux zones noires du motif, l’autre aux zones blanches. Bien sûr, les choses ne sont pas aussi binaires en art : bien souvent et selon son inspiration, une des deux couleurs sera remplacée par un mélange dans des proportions variables ou par une superposition des deux couleurs. De plus, au fur et à mesure du travail très minutieux (et très long) de peinture des motifs, d’autres couleurs vont émerger ici ou là, toujours selon l’inspiration de l’artiste, plus chaude à tel endroit pour souligner tel ou tel motif, plus froide ailleurs, et le tableau va progressivement apparaître sur la toile.

Figure 10 : les tableaux Garden Raga, Golden orbweaver et Stripe breaks, acrylique sur toile, Reg Alcorn

Crédits Reg Alcorn

L’effet visuel résultant de ces choix peut être tout à fait déconcertant : en taille réelle, les couleurs des différents motifs vibrent, se superposent, semblent produire des effets de perspective, se mélangent à une certaine distance du tableau, au point qu’il est parfois difficile de croire ce qu’on voit et même d’en détacher son regard…

3.3. Variations

Le procédé expliqué ci-dessus permet de faire apparaître une très grande quantité de motifs différents. Un « atlas de séquences » recensant ces motifs est d’ailleurs en préparation. Cependant Reg Alcorn a aussi exploré des variantes du procédé pour obtenir d’autres effets. Par exemple en créant des tableaux à plusieurs centres, avec une spirale enroulée autour de chacun ; ou encore en remplaçant la tuile carrée de Truchet par des tuiles rectangulaires dont les deux moitiés délimitées par une diagonale sont dans les proportions du triangle de Pythagore de côtés 3, 4 et 5 (voire en alternant les deux types de tuiles). Dans le premier cas, les tableaux ainsi construits peuvent prendre une connotation figurative, surtout s’ils comportent cinq centres pouvant évoquer les quatre membres et la tête d’un animal ou d’un être humain ; dans le deuxième cas, des formes plus lisses apparaissent aux contours des motifs, tandis que les lignes de la spirale, donc le procédé de construction, sont plus visibles.

4. Retour sur la spirale d’Ulam

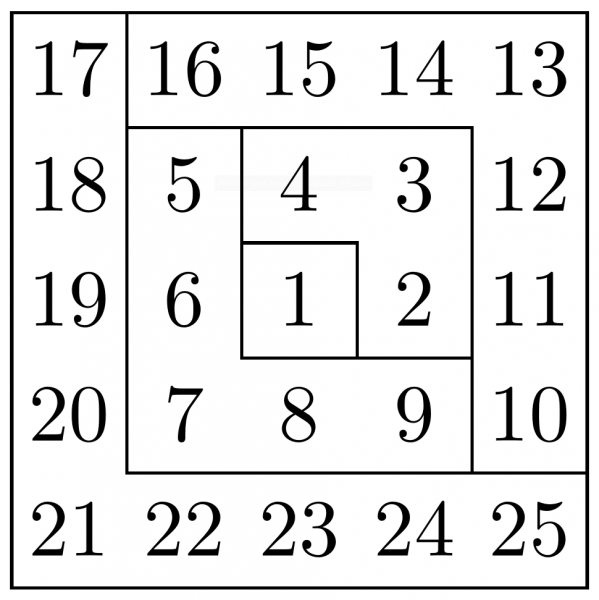
Imaginons qu’on enroule en spirale des carrés de côté 1, dans lesquels sont inscrits les entiers naturels à partir de 1 au centre. À chaque fois qu’on arrive sur le carré d’un entier (1 =1², 4 = 2², 9 = 3², 16 = 4²…), la figure obtenue est elle-même un carré, dont 1 est le centre s’il s’agit du carré d’un nombre impair (se trouvant alors dans le coin en bas à droite) ou bien se situe juste en dessous du centre pour le carré d’un nombre pair (qui lui se trouve dans le coin supérieur gauche du carré).

Figure 11 : les carrés dans la spirale d’Ulam

4.1. Repérage

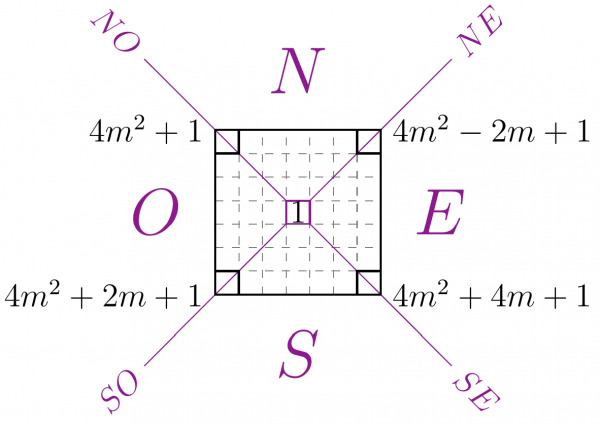
La remarque précédente donne accès à la forme générale des coins du carré de côté impair 2m+1, où m est un entier naturel, qui est donnée dans la Figure 12, où l’on fait apparaître de plus les directions de la rose des vents pour aider au repérage.

Figure 12 : les coins du carré de côté 2m+1

Le coin inférieur droit contient l’entier (2m + 1)² = 4m² + 4m + 1, les formules pour les autres coins s’en déduisent facilement en remontant la spirale.

4.2. Formule d’Euler

La fonction polynomiale

E(n) = n² + n + 41

est connue depuis le mathématicien suisse Euler (1707 – 1783) par le fait très remarquable qu’elle prend 40 valeurs premières consécutives : les nombres E(0) = 41, E(1) = 43, E(2) = 47, …, E(39) = 1601 sont tous des nombres premiers. Il a fallu attendre la fin du XX^e siècle pour que les mathématiciens Fung en 1988 puis Ruby en 1989 trouvent des polynômes prenant un plus grand nombre de valeurs premières consécutives (respectivement 43 et 45, record actuel, voir Dress et Olivier, 1999, pour des détails). Ulam et ses co-auteurs ont également vérifié que la formule d’Euler prend 47,5 % de valeurs premières jusqu’à 10 000 000.

Or, les valeurs de la formule d’Euler aux entiers impairs et aux entiers pairs peuvent s’écrire comme suit :

E(2m - 1) = (4m² - 2m + 1) + 40

E(2m) = (4m² +2m + 1) + 40

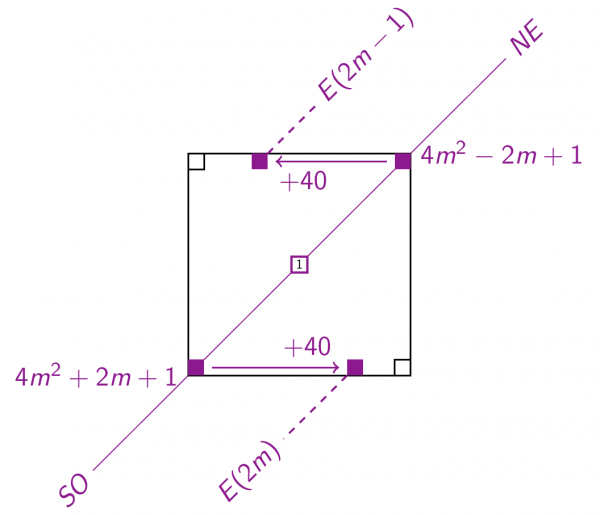
ce qui signifie que les valeurs de la formule d’Euler aux entiers impairs se trouvent, pour m assez grand, sur une parallèle à la demi-diagonale NE, tandis que celles aux entiers pairs sont sur une parallèle à la demi-diagonale SO, comme indiqué en Figure 13.

Figure 13 : les valeurs de la formule d’Euler aux entiers pairs et impairs dans la spirale d’Ulam

4.3. Ulam et Euler et ...

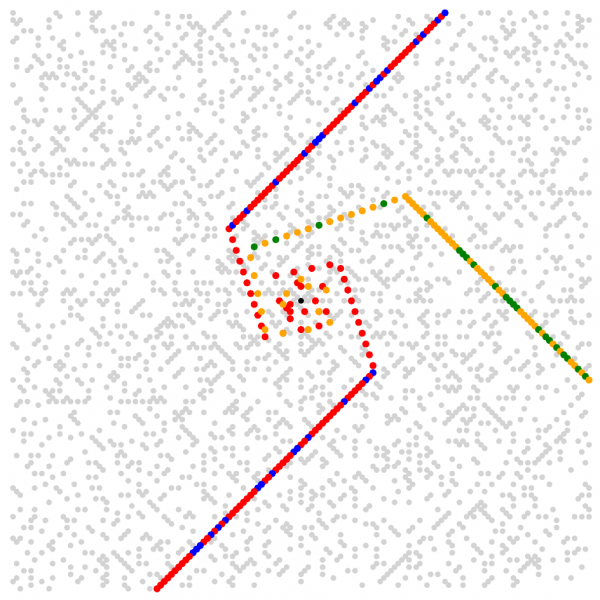
La Figure 14 montre les valeurs de la formule d’Euler dans la spirale d’Ulam, avec 1 au centre en noir, en gris les nombres premiers, en rouge les valeurs premières de E(n), en bleu les autres valeurs, pour n jusqu’à 160.

Figure 14 : valeurs de polynômes dans la spirale d’Ulam

La Figure 14 fait également apparaître les valeurs d’un autre polynôme prenant un grand nombre de valeurs premières :

4n² + 4n + 59

pour n jusqu’à 80, avec les valeurs premières en orange, les autres en vert. On constate que les alignements visibles dans la spirale d’Ulam proviennent de certaines fonctions polynomiales prenant de nombreuses valeurs premières, l’orientation des alignements étant déterminé par la forme de ces fonctions. Ici on obtient des parallèles aux demi-diagonales NE et SO avec la formule d’Euler, à la demi-diagonale SE avec l’autre formule.

Même si les directions diagonales semblent prédominer sur la Figure 6, d’autres directions d’alignements sont possibles dans la spirale d’Ulam, notamment horizontales. Dans un article en préparation (Vinatier, 2023), on donne la forme générale des polynômes dont les valeurs forment des alignements dans la spirale. Cependant, la plupart d’entre eux ne prennent pas suffisamment de valeurs premières pour que ces alignements apparaissent dans la Figure 6. Réciproquement, de nombreuses fonctions polynomiales connues pour prendre un grand nombre de valeurs premières ne sont pas de cette forme et ne produisent donc pas d’alignements visibles… La représentation du plan à travers la spirale d’Ulam sélectionne visuellement certaines fonctions prenant un grand nombre de valeurs premières et laisse les autres dans l’ombre.