Second year

In this page you will find the description of the different second-year trainings offered within the Master ACSYON.

The three trainings of the second year of the Master Acsyon

Click on the boxes above to discover the corresponding training :

Local M2

This training is dedicated to english-speaker students willing to pursue their academic training at the University of Limoges. All courses are given in english and at the University of Limoges.

EUR M2

This training is dedicated to english-speaker students. It is a variant of the local training, with a special option related to the TACTIC Graduate School. It is the natural follow-up of the EUR M1 training. All courses are given in english at the University of Limoges.

MIX M2

This training is dedicated to french- and english-speaker students. It is the follow-up of the MIX M1 training. This training is addressed to students of the mechatronic training of ENSIL-ENSCI in Limoges. Three courses are delivered in english at the University of Limoges ; the rest of the training is ensured by ENSIL-ENSCI in Limoges, within the mechatronic training.

List of courses offered by M2 ACSYON

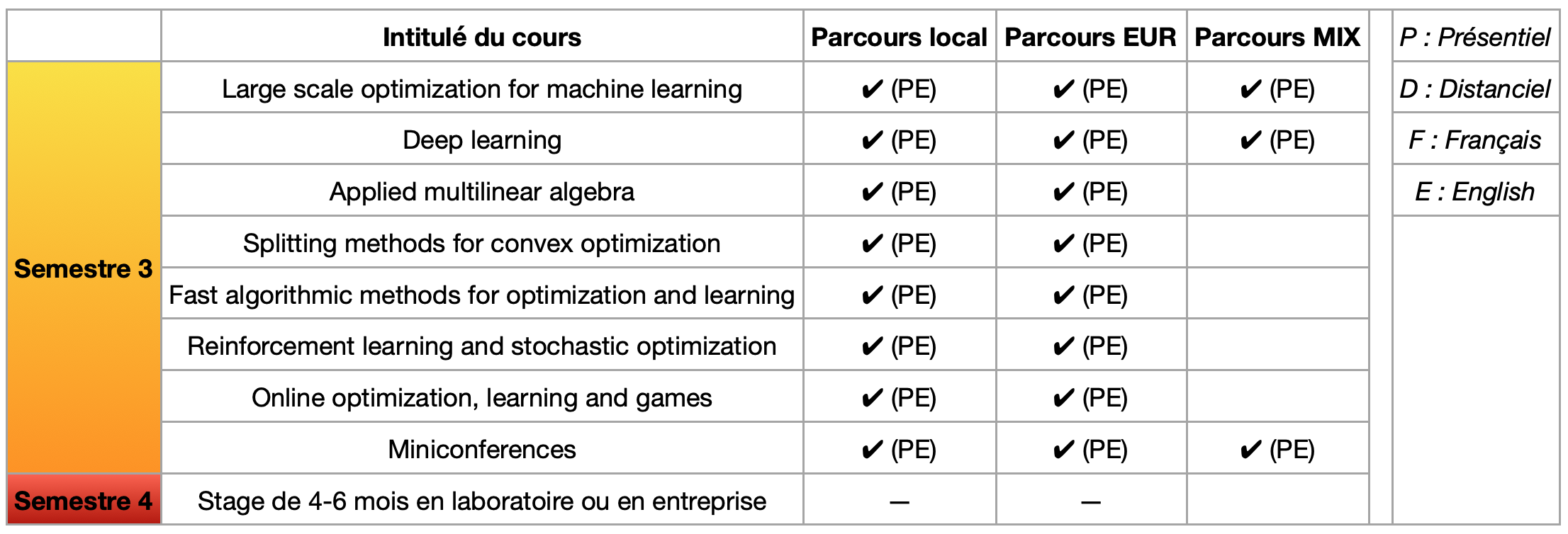
Description of the courses of the third semester

Optimization for large-scale machine learning

The course deals with large scale nonlinear optimization, in particular interior point methods for nonlinear optimization, SQP methods and first order methods (such as projected gradient and Frank-Wolfe). The second part deals with optimization algorithms that are use in the context of Big data & machine learning. The lecture focus on both the convergence theory and on the practical implementation aspect.

Prérequis
Optimization basics, linear algebra, convex geometry

Mots clés
Large-scale nonlinear optimization, big data optimization

Deep learning

Deep learning has become a must in artificial intelligence and more particularly in machine learning. The recent developments in machine translation, pattern recognition, speech recognition, autonomous driving and so on, are essentially due to the great advances made in this field. The goal of this course is to learn the basics of deep learning techniques and also to learn how to implement some elementary deep learning tasks. Each lesson will be followed by practical works with a Python3/JupyterLab environment, in order to use the deep learning tools as Tensorflow and Keras.

Prérequis
Basics on numerical linear algebra, differential calculus and machine learning basics, Python

Mots clés
Neural network, algorithm, supervised learning, unsupervised learning, gradient descent

Applied multilinear algebra

This course is a continuation of the M1 course “Applied linear algebra”, whose purpose is to present the algorithms and tools of matrix analysis necessary for machine learning and data processing. We will introduce the concepts and tools of multilinear algebra to analyze higher dimensional data. The latter are represented by tensors (multidimensional arrays) whose analysis can be done by methods generalizing matrix analysis techniques such as singular value decomposition. After the introduction of the mathematical formalism, the emphasis is put on the algorithmic aspects and applications.

Prérequis
Linear algebra, numerical matrix analysis, normed vector space, bilinear algebra, Euclidean spaces, differential calculus in R^n

Mots clés
Tensors, rank of tensors, singular value decomposition (HOSVD), tensor compression algorithm

Splitting methods for convex optimization

Chapter 0 recalls basics of convex analysis (such as projection and separation theorems, closed proper convex functions and Legendre-Fenchel conjugates). Chapter 1 explores fixed-point algorithms, as well as the relaxed Krasnoselskii-Mann algorihtm, for firmly nonexpansive and averaged operators (such as resolvents of maximal monotone operators). Applications are provided to projection operators with algorithms to solve convex feasibility problems. Chapter 2 introduces the classical notion of proximal operator associated to a closed proper convex function, which coincides with the resolvent of its subdifferential operator, and whose fixed points characterize its minimizers. The so-called proximal point algorithm is then invoked to solve convex minimization problems. In order to investigate sums and composites in the objective function, we investigate some well-known splitting methods, such as the proximal gradient algorithm (also called forward-backward algorithm) and the Douglas-Rachford algorithm. Finally Chapter 3 gives recalls on strong Lagrangian duality in convex inequality/equality constrained minimization problems and develops standard primal-dual methods, such as the method of multipliers or ADMM.

Several practical works (on Matlab or Pyhton) are performed during the semester in order to solve some standard problems that can be found in machine learning and data science, such as LASSO, consensus optimization, matrix decomposition problem, risk-averse optimization, clustering, image restoring (denoising, deblurring, inpainting), etc.

Prérequis
Convex analysis, topology, differential calculus, linear algebra and optimization basics

Mots clés
Maximal monotone set-values maps and resolvents, firmly non expansive and averaged operators, fixed-point algorithm, Krasnoselskii-Mann algorithm, projection operator, proximal operator, proximal point algorithm, proximal gradient algorithm (forward-backward), Douglas-Rachford algorithm, Davis-Yin algorithm, Lagrangian duality, primal-dual algorithms, method of multipliers, ADMM

Fast algorithmic methods for optimization and learning

The many challenges posed by the machine learning and the processing of big and noisy data require the development of new mathematical tools and fast algorithms in optimization. The course starts with the class of Iterative Shrinkage-Thresholding Algorithms (ISTA) and their application for solving linear inverse problems in signal processing. This class of methods can be viewed as extension of the classical gradient algorithm and is known to be attractive due to their simplicity and adequacy for solving large-scale problems in optimization. We study their convergence analysis and also show their slowness in some situations. The Fast-Iterative Shrinkage-Thresholding Algorithm (FISTA) was introduced by Beck and Teboulle in 2009. The convergence analysis of FISTA will be studied in this lecture as well as its comparison with ISTA on several examples.

The second part of this course will be devoted to the link between continuous differential equations and algorithms in optimization (obtained by explicit/implicit temporal discretization). This back and forth between continuous and discrete dynamics allowed us to propose efficient and fast algorithms in optimization. This include:

– damped inertial gradient method for understanding and extending Nesterov accelerated gradient method

– Hessian-driven damping for speeding up and damping oscillations of optimization algorithms,

– Fast algorithms in convex optimization based on inertial gradient-based dynamics

– Asymptotic vanishing damping and its link with Nesterov acceleration.

Applications will be given in image processing such as image denoising, image deconvolution, image inpainting, motion estimation and image segmentation.

Prérequis
Linear algebra, topology and differential calculus in R^n, convex analysis, optimization basics

Mots clés
First order optimization algorithms, ISTA, FISTA, Nesterov acceleration, damped inertial gradient methods, Hessian-driven damping algorithms, asymptotic vanishing damping

Reinforcement learning and stochastic optimization

We begin this course with the study of Markov decision processes. In this case, we assume that the decision-maker has full knowledge of the data of the problem and we talk about a model-based problem. Next, we drop this assumption, and we enter the realm of reinforcement learning problems, which loosely speaking means that the environment must be learnt from successive experiences. From the mathematical point of view, this can be done by using Monte-Carlo techniques, which will be studied in the course. In the second part of the course, we will present the theoretical foundations of stochastic optimization methods by introducing rigorously the so-called stochastic gradient descent and then proceeding to extend some standard first order algorithms in convex analysis to the case where randomness is present.

Prérequis
Optimization basics, practical optimization and stochastic processes

Online optimization, learning and games

This course is intended to provide a gentle introduction to algorithmic game theory. We will focus in particular on the connections between game theory, learning and online optimiztion, as well as some of the core applications of algorithmic game theory to machine learning (recommender systems, GANS, etc.).

Mots clés
Game theory, learning, optimization, gradient-based techniques

Miniconferences

The speakers for this series of conferences (scheduled to last from 1h30 to 3h) are chosen from among data science specialists in regional or national companies. The topics discussed may be related to the lectures provided in the ACSYON’s program, or on the contrary, on topics in the field of data science and artificial intelligence that are not (or only slightly) covered in the program.

Mots clés
Thematic conferences, practical cases, applied sciences, business