|
Title of the project:
HYPERSPACE Principal investigator: Simone Naldi (Maître de conférences, Université de Limoges, France) Period: 01/01/2022 — 31/12/2025 Keywords: Determinantal and spectrahedral representations Certificates of hyperbolicity, Generalized Lax Conjecture Computer algebra algorithms Complexity of semidefinite and hyperbolic programming |
|
|
Abstract:
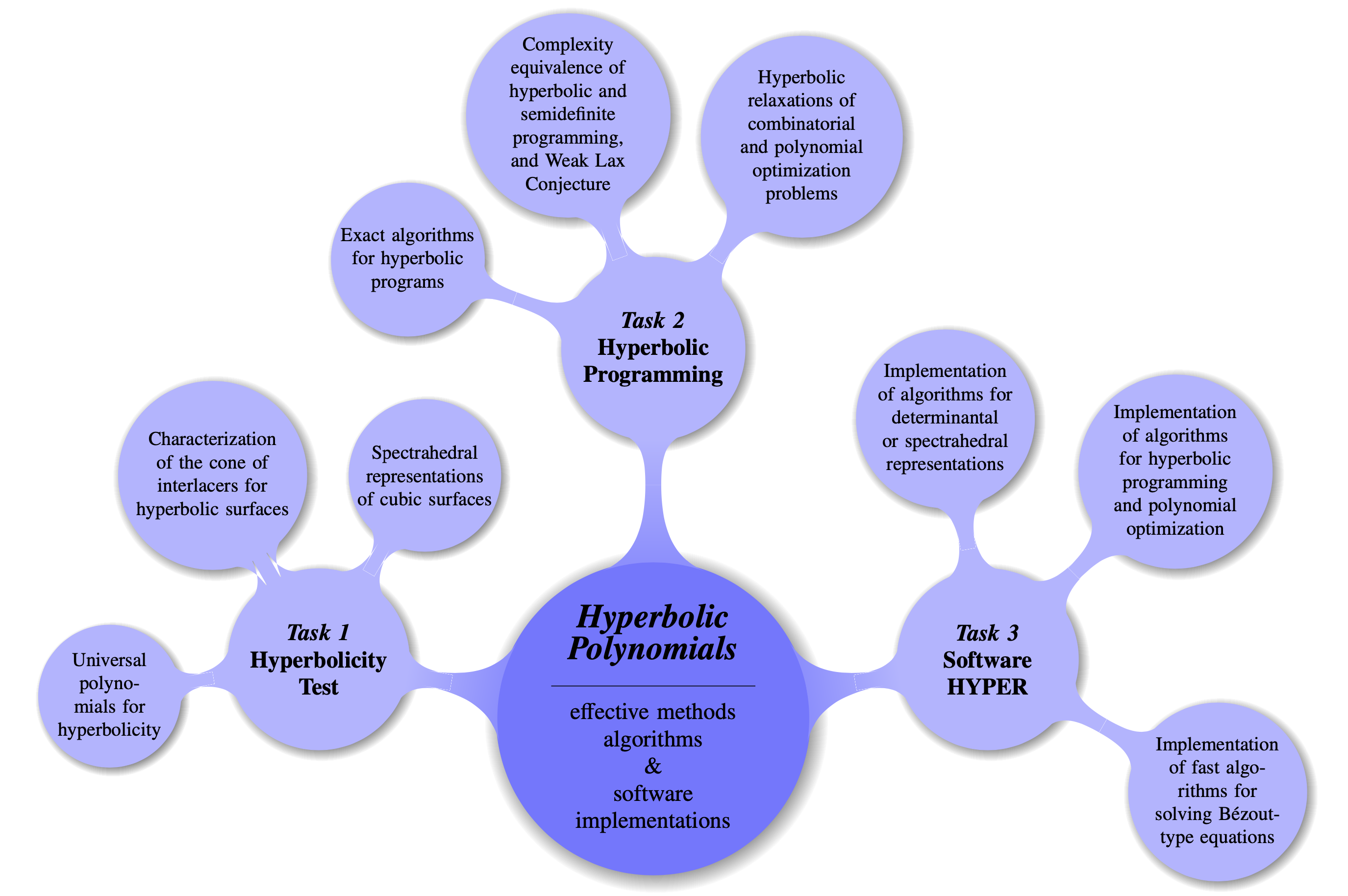
In the project HYPERSPACE we develop effective methods, algorithms and software dedicated to hyperbolic polynomials. These form a class of real multivariate polynomials of central interest in applied mathematics and computer science (because of their importance in polynomial optimization and control theory, just to name two applications). The major open question related to this theory is the so-called Generalized Lax Conjecture, concerned with the representability of hyperbolic polynomials by means of determinants of symmetric matrices. More generally, a challenge in terms of complexity is the problem of certifying whether a given multivariate polynomial is hyperbolic, in other words, the hyperbolicity test. Efficient algorithms and good complexity bounds as well as software implementations for hyperbolic polynomials are missing but considered crucial for the future development of this theory. The goal of our project HYPERSPACE is twofold: on the one hand we want to develop new effective methods and algorithms for hyperbolic polynomials, on the other hand we aim at implementing reliable software as a support to current and future research. Previous related work: M. Kummer, S. Naldi and D. Plaumann. Spectrahedral representations of plane hyperbolic curves, Pac. J. Math. 303(1):243--263 (2019) S. Naldi and D. Plaumann. Symbolic computation in hyperbolic programming, J. Algebra Appl. 17:10 (2018) |
Publications that acknowledge support by the ANR HYPERSPACE:
(C. Cornou, S. Naldi and T. Vaccon) Semidefinite representable sets over valuation rings. In preparation, 2025.
(S. Naldi and V. Neiger) Gröbner bases, syzygies and polynomial matrix multiplication. In preparation, 2025.
(D. Henrion and S. Naldi) Certifying moment semidefinite representations of convex semialgebraic sets. In preparation, 2025.
(M. Longinetti and S. Naldi) Sharp bounds for the sphere crossing radius of some families of tetrahedra. In preparation, 2025.
(S. Naldi, M. Safey El Din, A. Taylor and W. Wang) Solving generic parametric linear matrix inequalities. February 2025, arXiv/2503.01487, submitted.
(M. Longinetti, S. Naldi and A. Venturi) R-hulloid of the vertices of a tetrahedron. June 2024, arXiv/2406.00658, submitted.
(M. Longinetti and S. Naldi) On the configurations of four spheres supporting the vertices of a tetrahedron. May 2024, arXiv/2405.16167, submitted.
(V. Kolmogorov, S. Naldi and J. Zapata) Verifying feasibility of degenerate semidefinite programs. May 2024, arXiv/2405.13625, submitted.
(A. Conca, S. Naldi, G. Ottaviani and B. Sturmfels) Taylor polynomials of rational functions. Acta Math. Vietn. (2023) [full-text view-only]
(D. Henrion, S. Naldi and M. Safey El Din) Algebraic certificates for the truncated moment problem. arXiv/2302.06927
Activities funded by the ANR HYPERSPACE:
Invitation of V. Neiger (Lip6, Sorbonne Univ.) at XLIM (Limoges) on 17-21/01/2022
Organisation of the workshop Structured Matrix Days at XLIM (Limoges) on 19-20/05/2022 (cofunded by Instit. XLIM and GdR IM)
Participation of S. Naldi to MFO Oberwolfach Real Algebraic Geometry with a View toward Koopman Operator Methods, 03/2023
Participation of S. Naldi to SIAM Conference in Applied Algebraic Geometry (Eindhoven, 07/2023)
Invitation of J. Zapata (IST Austria) at XLIM (Limoges) on 02/2022 and in Lip6 (Paris) on 10/2023
Participation of S. Naldi to the Chow Lectures at MPI Leipzig, 10/2023
Visit of S. Naldi to F. Gesmundo (IMT, Toulouse) and D. Henrion (LAAS CNRS, Toulouse) in March 2025.
Participation of S. Naldi to SIAM AG 2025, Madison (USA), July 2025.
Participation of S. Naldi to ISSAC 2025, Guanajuato (Mexico), August 2025.
Funding:
