|
|
|
Last updated : 24 August 2005
This page shows some examples of contour plots obtained with FreeBasic and the FBMath library.
The contouring routine ConRec implemented in FBMath is an adaptation of an algorithm developed by Paul Bourke. The code is the following (file plotcont.bas in FBMath):
' ******************************************************************
' CONREC - A Contouring Routine
' by Paul Bourke, Byte, June 1987
' http://astronomy.swin.edu.au/~pbourke/projection/conrec/
' Adapted to FreeBasic by "Thulefoth"
' Modified by J. Debord for inclusion in the FreeBasic Math library
' http://sourceforge.net/projects/fbmath
' ******************************************************************
' ------------------------------------------------------------------
' Global variable
' ------------------------------------------------------------------
COMMON SHARED ErrCode AS INTEGER
' Error code from the latest function evaluation
' ******************************************************************
OPTION EXPLICIT
SUB ConRec (X() AS INTEGER, _
Y() AS INTEGER, _
Z() AS DOUBLE, _
D() AS DOUBLE, _
Col() AS INTEGER)
' ------------------------------------------------------------------
' Input parameters:
' X(0..IUb), Y(0..JUb) = point coordinates in pixels
' D(0..IUb, 0..JUb) = function values
' D(I,J) is the function value at (X(I), Y(I))
' Z(0..(Nc - 1)) = Contour levels in increasing order
' Col(0..(Nc - 1)) = Colour table
' ------------------------------------------------------------------
' Check the input parameters for validity
CONST True = -1, False = 0
DIM AS INTEGER PrmErr = False
DIM AS INTEGER IUb, JUb, Nc, I, J, K, M, M1, M2, M3
DIM AS DOUBLE Dmin, Dmax, X1, X2, Y1, Y2
ErrCode = 0
IUb = UBOUND(X)
JUb = UBOUND(Y)
Nc = UBOUND(Z) + 1
IF IUb <= 0 OR UBOUND(D, 1) <> IUb THEN PrmErr = True
IF JUb <= 0 OR UBOUND(D, 2) <> JUb THEN PrmErr = True
IF Nc <= 0 THEN PrmErr = True
FOR K = 1 TO Nc - 1
IF Z(K) <= Z(K - 1) THEN PrmErr = True
NEXT K
IF PrmErr THEN ErrCode = -1: EXIT SUB
DIM AS DOUBLE H(0 TO 4) ' Relative heights of the box above contour
DIM AS INTEGER Ish(0 TO 4) ' Sign of H()
DIM AS INTEGER Xh(0 TO 4) ' X coordinates of box
DIM AS INTEGER Yh(0 TO 4) ' Y coordinates of box
' Mapping from vertex numbers to X offsets
DIM AS INTEGER Im(0 TO 3) = {0, 1, 1, 0}
' Mapping from vertex numbers to Y offsets
DIM AS INTEGER Jm(0 TO 3) = {0, 0, 1, 1}
' Case switch table
DIM AS INTEGER CasTab(0 TO 2, 0 TO 2, 0 TO 2) = _
{{0,0,8}, {0,2,5}, {7,6,9}, _
{0,3,4}, {1,3,1}, {4,3,0}, _
{9,6,7}, {5,2,0}, {8,0,0}}
' Scan the array, top down, left to right
FOR J = JUb - 1 TO 0 STEP -1
FOR I = 0 TO IUb - 1
' Find the lowest vertex
IF D(I, J) < D(I, J + 1) THEN Dmin = D(I, J) ELSE Dmin = D(I, J + 1)
IF D(I + 1, J) < Dmin THEN Dmin = D(I + 1, J)
IF D(I + 1, J + 1) < Dmin THEN Dmin = D(I + 1, J + 1)
' Find the highest vertex
IF D(I, J) > D(I, J + 1) THEN Dmax = D(I, J) ELSE Dmax = D(I, J + 1)
IF D(I + 1, J) > Dmax THEN Dmax = D(I + 1, J)
IF D(I + 1, J + 1) > Dmax THEN Dmax = D(I + 1, J + 1)
IF Dmax < Z(0) OR Dmin > Z(Nc - 1) THEN GOTO NoneInBox
' Draw each contour within this box
FOR K = 0 TO Nc - 1
IF Z(K) < Dmin OR Z(K) > Dmax THEN GOTO NoneInTri
FOR M = 4 TO 0 STEP -1
IF M > 0 THEN
H(M) = D(I + Im(M - 1), J + Jm(M - 1)) - Z(K)
Xh(M) = X(I + Im(M - 1))
Yh(M) = Y(J + Jm(M - 1))
END IF
IF M = 0 THEN
H(0) = (H(1) + H(2) + H(3) + H(4)) / 4
Xh(0) = (X(I) + X(I + 1)) / 2
Yh(0) = (Y(J) + Y(J + 1)) / 2
END IF
IF H(M) > 0 THEN Ish(M) = 2
IF H(M) < 0 THEN Ish(M) = 0
IF H(M) = 0 THEN Ish(M) = 1
NEXT M
' Scan each triangle in the box
FOR M = 1 TO 4
M1 = M: M2 = 0: M3 = M + 1
IF M3 = 5 THEN M3 = 1
SELECT CASE CasTab(Ish(M1), Ish(M2), Ish(M3))
CASE 0
GOTO Case0
' Line between vertices M1 and M2
CASE 1
X1 = Xh(M1): Y1 = Yh(M1): X2 = Xh(M2): Y2 = Yh(M2)
' Line between vertices M2 and M3
CASE 2
X1 = Xh(M2): Y1 = Yh(M2): X2 = Xh(M3): Y2 = Yh(M3)
' Line between vertices M3 and M1
CASE 3
X1 = Xh(M3): Y1 = Yh(M3): X2 = Xh(M1): Y2 = Yh(M1)
' Line between vertex M1 and side M2-M3
CASE 4
X1 = Xh(M1): Y1 = Yh(M1)
X2 = (H(M3) * Xh(M2) - H(M2) * Xh(M3)) / (H(M3) - H(M2))
Y2 = (H(M3) * Yh(M2) - H(M2) * Yh(M3)) / (H(M3) - H(M2))
' Line between vertex M2 and side M3-M1
CASE 5
X1 = Xh(M2): Y1 = Yh(M2)
X2 = (H(M1) * Xh(M3) - H(M3) * Xh(M1)) / (H(M1) - H(M3))
Y2 = (H(M1) * Yh(M3) - H(M3) * Yh(M1)) / (H(M1) - H(M3))
' Line between vertex M3 and side M1-M2
CASE 6
X1 = Xh(M3): Y1 = Yh(M3)
X2 = (H(M2) * Xh(M1) - H(M1) * Xh(M2)) / (H(M2) - H(M1))
Y2 = (H(M2) * Yh(M1) - H(M1) * Yh(M2)) / (H(M2) - H(M1))
' Line between sides M1-M2 and M2-M3
CASE 7
X1 = (H(M2) * Xh(M1) - H(M1) * Xh(M2)) / (H(M2) - H(M1))
Y1 = (H(M2) * Yh(M1) - H(M1) * Yh(M2)) / (H(M2) - H(M1))
X2 = (H(M3) * Xh(M2) - H(M2) * Xh(M3)) / (H(M3) - H(M2))
Y2 = (H(M3) * Yh(M2) - H(M2) * Yh(M3)) / (H(M3) - H(M2))
' Line between sides M2-M3 and M3-M1
CASE 8
X1 = (H(M3) * Xh(M2) - H(M2) * Xh(M3)) / (H(M3) - H(M2))
Y1 = (H(M3) * Yh(M2) - H(M2) * Yh(M3)) / (H(M3) - H(M2))
X2 = (H(M1) * Xh(M3) - H(M3) * Xh(M1)) / (H(M1) - H(M3))
Y2 = (H(M1) * Yh(M3) - H(M3) * Yh(M1)) / (H(M1) - H(M3))
' Line between sides M3-M1 and M1-M2
CASE 9
X1 = (H(M1) * Xh(M3) - H(M3) * Xh(M1)) / (H(M1) - H(M3))
Y1 = (H(M1) * Yh(M3) - H(M3) * Yh(M1)) / (H(M1) - H(M3))
X2 = (H(M2) * Xh(M1) - H(M1) * Xh(M2)) / (H(M2) - H(M1))
Y2 = (H(M2) * Yh(M1) - H(M1) * Yh(M2)) / (H(M2) - H(M1))
END SELECT
LINE (X1, Y1)-(X2, Y2), Col(K)
Case0:
NEXT M
NoneInTri:
NEXT K
NoneInBox:
NEXT I
NEXT J
END SUB
|
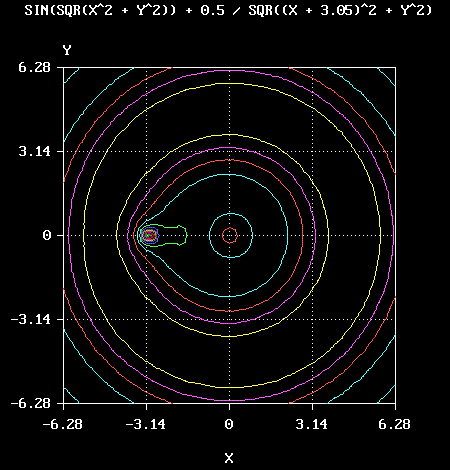
An example program is shown below (file contour.bas in FBMath).
The example function is:
|
where c is a constant which may be varied to modify the aspect of the graph (the example used c = 3.05).
' ******************************************************************
' Contour plot of a two-dimensional function
' ******************************************************************
#include "math.bi"
#include "fbgfx.bi"
' ******************************************************************
OPTION EXPLICIT
' ******************************************************************
' Define here the function to be plotted
' ******************************************************************
CONST FuncName = "SIN(SQR(X^2 + Y^2)) + 0.5 / SQR((X + 3.05)^2 + Y^2)"
FUNCTION Func(X AS DOUBLE, Y AS DOUBLE) AS DOUBLE
' Function to be plotted
CONST C = 3.05
DIM AS DOUBLE X2, Y2, Xc, Xc2
X2 = X * X
Y2 = Y * Y
Xc = X + C
Xc2 = Xc * Xc
Func = SIN(SQR(X2 + Y2)) + 0.5 / SQR(Xc2 + Y2)
END FUNCTION
' ******************************************************************
' Main program
' ******************************************************************
' Initialize screen (Screen 12 with white on black here)
IF NOT InitScreen(12, 15, 0) THEN STOP
' Set number of contours (colours) according to the screen resolution
CONST Nc = 15
' Define colours
DIM AS INTEGER Col(0 TO Nc - 1), I
FOR I = 0 TO Nc - 1
Col(I) = Nc - I
NEXT I
' Set scale
CONST Xmin = - TwoPi, Xmax = TwoPi, Xstep = Pi
CONST Ymin = - TwoPi, Ymax = TwoPi, Ystep = Pi
' Set graphic area (here it will look approximately square)
InitGraph 24, 76, 15, 85
' Set number of grid points
CONST NpX = 60
CONST NpY = 60
' Dimension variables
DIM AS INTEGER J ' Loop variable
DIM AS DOUBLE Dx, Dy ' Increments of X and Y
DIM AS DOUBLE Dmin, Dmax ' Min. and max. function values
DIM AS DOUBLE H ' Increment for levels
DIM AS DOUBLE Xu(0 TO NpX), Yu(0 TO NpY) ' Point coordinates in user units
DIM AS INTEGER Xp(0 TO NpX), Yp(0 TO NpY) ' Point coordinates in pixels
DIM AS DOUBLE D(0 TO NpX, 0 TO NpY) ' Function values
DIM AS DOUBLE Z(0 TO Nc - 1) ' Contour array
' Set scales and plot axes
SetOxScale LinScale, Xmin, Xmax, Xstep
SetOyScale LinScale, Ymin, Ymax, Ystep
PlotOxAxis Ymin, 2
PlotOyAxis Xmin, 2
PlotGrid BothGrid
WriteTitles FuncName, "X", "Y"
' Generate grid points
Dx = (Xmax - Xmin) / NpX
Dy = (Ymax - Ymin) / NpY
Xu(0) = Xmin
FOR I = 1 TO NpX
Xu(I) = Xu(I - 1) + Dx
NEXT I
Yu(0) = Ymin
FOR J = 1 TO NpY
Yu(J) = Yu(J - 1) + Dy
NEXT J
FOR I = 0 TO NpX
Xp(I) = Xpixel(Xu(I))
NEXT I
FOR J = 0 TO NpY
Yp(J) = Ypixel(Yu(J))
NEXT J
' Compute function values
Dmin = Func(Xmin, Ymin)
Dmax = Dmin
FOR I = 0 TO NpX
FOR J = 0 TO NpY
D(I,J) = Func(Xu(I), Yu(J))
IF D(I,J) < Dmin THEN
Dmin = D(I,J)
ELSEIF D(I,J) > Dmax THEN
Dmax = D(I,J)
END IF
NEXT J
NEXT I
' Define levels
Z(0) = Dmin
H = (Dmax - Dmin) / (Nc - 1)
FOR I = 1 TO Nc - 1
Z(I) = Z(I - 1) + H
NEXT I
' Plot contour
ConRec Xp(), Yp(), Z(), D(), Col()
SLEEP
END
|
This program produced the following image:

|
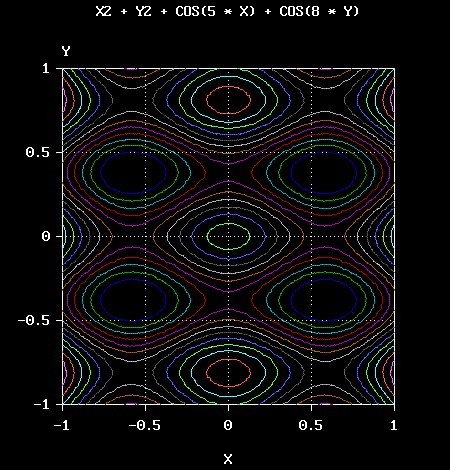
Another example, with a function having multiple minima and maxima:
where a and b are constants.
In the case (a = 5, b = 8), the previous program should be modified according to the following code:
CONST FuncName = "X2 + Y2 + COS(5 * X) + COS(8 * Y)" FUNCTION Func(X AS DOUBLE, Y AS DOUBLE) AS DOUBLE ' Function to be plotted DIM AS DOUBLE X2, Y2 X2 = X * X Y2 = Y * Y Func = X2 + Y2 + COS(5 * X) + COS(8 * Y) END FUNCTION CONST Xmin = - 1, Xmax = 1, Xstep = 0.5 CONST Ymin = - 1, Ymax = 1, Ystep = 0.5 |
and the output of the program would be the following:
|
You can create interesting effects by: