|
|
Je remercie Don Cross d'avoir autorisé la traduction de ce document. Le site original étant actuellement (et, je l'espère, temporairement) indisponible, j'ai supprimé la plupart des liens qui le concernaient.
Si vous avez besoin de calculer à la fois le sinus et le cosinus d'un angle variant régulièrement, voyez les deux sections suivantes.
Si vous ne voulez que le sinus ou le cosinus, mais pas les deux, voyez la Section 4.

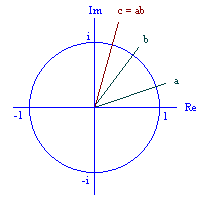
L'interprétation géométrique de la multiplication des nombres complexes nous montre comment faire tourner un nombre complexe autour de l'origine simplement en le multipliant par un autre nombre complexe. Le prix à payer réside dans la complexité des formules algébriques usuelles :
Re{c} = Re{a}Re{b} - Im{a}Im{b}
Im{c} = Re{a}Im{b} + Im{a}Re{b}
Si nous multiplions deux nombres complexes de module 1, le résultat a également un module de 1, mais son argument sera modifié. Nous pouvons répéter cela. Nous avons besoin des fonctions trigonométriques pour l'angle de départ et l'incrément d'angle. Ensuite, nous pouvons simplement utiliser les opérations de multiplication, addition, et soustraction en virgule flottante. La partie réelle du nombre complexe est le cosinus de l'argument, et la partie imaginaire est le sinus. Notez que le sinus aussi bien que le cosinus sont disponibles à chaque itération, que vous ayez besoin des deux ou pas. Même si vous n'en voulez qu'un, cette méthode reste beaucoup plus rapide que son équivalent en fonctions trigonométriques.
Voici un petit programme C pour illustrer cette méthode. Ce programme demande à l'utilisateur un angle de départ a0 et un incrément angulaire da. Il imprime ensuite une table des sinus et cosinus des 20 premiers angles a = a0 + k*da, où k = 0, 1, 2, ..., 19.
/* trig1.c - Programme exemple par Don Cross <dcross@intersrv.com> */
/* http://www.intersrv.com/~dcross/fasttrig.html */
#include <stdio.h>
#include <math.h>
#define PI (3.14159265358979323846)
int main (void)
{
double a, da, a0_rad, da_rad;
double a_sin, a_cos, da_sin, da_cos;
double temp;
int k;
printf ( "Entrez l'angle de depart en degres: " );
scanf ( "%lf", &a );
a0_rad = a * PI / 180.0; /* convertit en radians */
printf ( "Entrez l'increment angulaire en degres: " );
scanf ( "%lf", &da );
da_rad = da * PI / 180.0; /* convertit en radians */
a_cos = cos(a0_rad);
a_sin = sin(a0_rad);
da_cos = cos(da_rad);
da_sin = sin(da_rad);
printf ( "\n%15s %15s %15s\n", "angle", "cosinus", "sinus" );
printf ( "--------------- --------------- ---------------\n" );
for ( k=0; k<20; k++ )
{
printf ( "%15.5lf %15.7lf %15.7lf\n", a, a_cos, a_sin );
/* Voici le code qui met a jour les fonctions trigo... */
temp = a_cos*da_cos - a_sin*da_sin;
a_sin = a_cos*da_sin + a_sin*da_cos;
a_cos = temp;
/* Mettre a jour l'angle pour l'affichage. */
/* Cette etape n'a pas d'influence sur les fonctions trigo. */
a += da;
}
return 0;
}
/*--- fin du fichier trig1.c ---*/
|
Voici un raffinement de la technique précédente que j'ai pris dans l'ouvrage Numerical Recipes in Fortran par Press, Teukolsky, Vetterling, and Flannery, publié par Cambridge University Press. Il est un peu plus compliqué, mais pour une raison quelconque (que je ne comprends pas vraiment), il entraîne beaucoup moins d'erreurs d'arrondi cumulatives lors d'un grand nombre d'itérations. Sur mon ordinateur, l'erreur d'arrondi (sur le module du vecteur) avec la première méthode est de l'ordre de 10-10 (une partie pour dix milliards) après environ 1000 itérations, tandis qu'avec cette méthode l'erreur est de l'ordre de 10-14 (une partie pour 100 000 milliards). La plupart du temps, je ne m'en soucie pas, et donc j'utilise la première méthode car elle est plus facile à mémoriser. Mais si la précision est absolument critique, utilisez cette approche.
/* trig2.c - Programme exemple par Don Cross <dcross@intersrv.com> */
/* http://www.intersrv.com/~dcross/fasttrig.html */
#include <stdio.h>
#include <math.h>
#define PI (3.14159265358979323846)
int main (void)
{
double a, da, a0_rad, da_rad;
double a_sin, a_cos, alpha, beta;
double temp;
int k;
printf ( "Entrez l'angle de depart en degres: " );
scanf ( "%lf", &a );
a0_rad = a * PI / 180.0; /* convertit en radians */
printf ( "Entrez l'increment angulaire en degres: " );
scanf ( "%lf", &da );
da_rad = da * PI / 180.0; /* convertit en radians */
a_cos = cos(a0_rad);
a_sin = sin(a0_rad);
alpha = sin(0.5 * da_rad);
alpha = 2.0 * alpha * alpha;
beta = sin(da_rad);
printf ( "\n%15s %15s %15s\n", "angle", "cosinus", "sinus" );
printf ( "--------------- --------------- ---------------\n" );
for ( k=0; k<20; k++ )
{
printf ( "%15.5lf %15.7lf %15.7lf\n", a, a_cos, a_sin );
/* Voici le code qui met a jour les fonctions trigo... */
temp = a_cos - (alpha*a_cos + beta*a_sin);
a_sin = a_sin - (alpha*a_sin - beta*a_cos);
a_cos = temp;
/* Mettre a jour l'angle pour l'affichage. */
/* Cette etape n'a pas d'influence sur les fonctions trigo. */
a += da;
}
return 0;
}
/*--- fin du fichier trig2.c ---*/
|
La formule suivante est la plus rapide et la plus précise que j'aie vue pour calculer une sinusoïde unique. Elle requiert seulement une multiplication et une soustraction par itération. Pour calculer yn = sin(nW + B), utilisez la formule suivante :
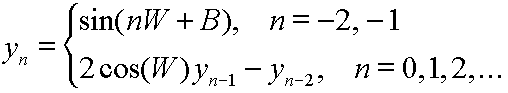
Notez qu'il vous faut calculer les deux valeurs y-2 et y-1 pour démarrer. De plus, vous devez pré-calculer la valeur de 2*cos(W) et la mémoriser dans une variable qui sera appelée dans la boucle de calcul.
Voici une démonstration de cette formule. Rappelez-vous l'équation de l'exponentielle complexe :
Cette formule représente un nombre complexe de module 1 et d'argument x radians. Le cosinus de l'angle est la partie réelle (axe horizontal) et le sinus est la partie imaginaire (axe vertical).
Soit z[n] un tableau de nombres complexes, avec n = 0, 1, 2, 3, ..., défini comme suit :
Ainsi z[n] est un nombre complexe de module 1 tournant autour de l'origine. Nous appelerons phaseur un tel nombre complexe tournant à vitesse fixe. Le phaseur démarre à B radians quand n = 0, et tourne de W radians par étape ensuite. L'astuce de la démonstration consiste à considérer la somme z[n+1] + z[n-1], c'est-à-dire la somme des valeurs encadrant une valeur donnée z[n].
z[n+1] + z[n-1]
= exp(i(n+1)W + iB) + exp(i(n-1)W + iB)
= exp(inW + iW + iB) + exp(inW - iW + iB)
= exp(inW + iB) exp(iW) + exp(inW + iB) exp(-iW)
= z[n] exp(iW) + z[n] exp(-iW)
= z[n] (exp(iW) + exp(-iW))
= z[n] (cos(W) + i sin(W) + cos(-W) + i sin(-W))
= z[n] (cos(W) + i sin(W) + cos(W) - i sin(W))
= 2 cos(W) z[n]
Nous savons donc que :
z[n+1] + z[n-1] = 2 cos(W) z[n]
Et par soustraction nous obtenons :
z[n+1] = 2 cos(W) z[n] - z[n-1]
Comparez cette dernière formule avec la formule ci-dessus, et vous verrez qu'elle décrit simultanément une fonction cosinus (partie réelle) et une fonction sinus (partie imaginaire). L'une ou l'autre peut être utilisée pour tracer une fonction sinusoïdale.
Voici un petit programme exemple en C++.
#include <iomanip.h>
#include <math.h>
const double PI = 3.14159265358979323846;
int main()
{
cout << "Entrez W en degres: " << flush;
double w;
cin >> w;
w *= PI / 180.0; // convertit en radians
cout << "Entrez B en degres: " << flush;
double b;
cin >> b;
b *= PI / 180.0; // convertit en radians
double y[3];
y[0] = sin(-2*w + b);
y[1] = sin(-w + b);
const double p = 2.0 * cos(w);
for ( int i=0; i<40; i++ )
{
y[2] = p*y[1] - y[0];
y[0] = y[1];
y[1] = y[2];
cout << setprecision(10) << y[2] << endl;
}
return 0;
}
|