Montrer des savoirs mathématiques ?
Les illustrations dans des manuels scolaires d’arithmétique et de travaux manuels de la Troisième République Showing mathematical knowledge ?
Illustrations in some textbooks in arithmetic and handwork during the French Third Republic

« Ne conviendrait-il pas de réformer l’imagerie scolaire et enfantine et d’en tirer tous les services qu’elle peut rendre indirectement à l’instruction populaire ? » (Gresse, 1887 : 1320)

I. Définitions, choix et méthodologie

Que sont ces savoirs mathématiques ? Margolinas définit un savoir comme « une construction sociale et culturelle, qui vit dans une institution (…) Le savoir est dépersonnalisé, décontextualisé, détemporalisé. Il est formulé, formalisé, validé et mémorisé. Il peut être linéarisé, ce qui correspond à sa nature textuelle. » (Margolinas, 2012 : 2). Les savoirs mathématiques constituent alors des constructions élaborées tout à la fois par des mathématicien.ne.s (Margolinas, 2012) producteurs des savoirs savants, et par des politiques et ministres qui définissent les limites de ces savoirs à enseigner dans chaque discipline. Tous les acteurs qui participent à la scolarisation des savoirs savants œuvrent également à ce processus, qu’il s’agisse des auteur.e.s qui proposent des interprétations des savoirs à apprendre à travers les manuels qu’ils/elles rédigent, ou encore des enseignant.e.s qui font vivre les savoirs mathématiques dans leur pratique quotidienne (Moreira, David, 2003). Dans l’école primaire de la Troisième République, ces savoirs mathématiques sont présents dans différentes disciplines : l’arithmétique, la géométrie, le dessin linéaire, ainsi que les travaux manuels (Rodrigues Valente, 2015).

A. Arithmétique et travaux manuels à l’école primaire

Pendant le XIX^e siècle, le rôle de l’arithmétique est de faire évoluer les pratiques populaires en matière de calcul décimal et particulièrement de diffuser et de généraliser l’utilisation du système légal des poids et mesures (Galisson, 2008) Avec l’avènement de la Troisième République, le calcul devient un des champs de savoirs explicitement développé dans l’Arrêté du 27 juillet 1882 réglant l'organisation pédagogique et le plan d'études des écoles primaires publiques, pour les trois cours de l’école primaire. Des manuels scolaires d’arithmétique spécialement destinés aux écoles primaires ont commencé à apparaître dès les premières décennies du XIX^e siècle, présentant une organisation des savoirs et savoir-faire à s’approprier pour les élèves. Leur nombre augmente considérablement tout au long du XIX^e siècle (Legros, 2018 à paraître).

Le travail manuel, quant à lui, est introduit comme une discipline de l’enseignement primaire français dans les Instructions officielles de juillet 1882. Il s’inscrit alors dans cet amalgame de disciplines et connaissances établies pour et par l’école décrit par Warde (2014). Au début de la Troisième République, la reconnaissance de l’utilité du travail manuel à l’école primaire est unanime, même si ses objectifs sont discutés. Les uns valorisent la préparation directe à un métier donc une dimension préprofessionnelle, alors que d’autres cherchent à préparer les enfants à des aptitudes et qualités dont ils auront besoin dans leur vie future, personnelle et le cas échéant professionnelle, par exemple, des habitudes d’attention, d’application, de persévérance, d’ordre, de précision, d’exactitude, de dextérité (Schmitt, 1888). Ils servent d’auxiliaire à l’enseignement général en requérant des connaissances acquises dans d’autres champs de savoir : « le système métrique, les éléments de la géométrie, les notions de physique et des sciences naturelles » (Schmitt, 1888). Le travail manuel se consolide comme matière scolaire car il participe de l’éducation globale de l’enfant, à l'articulation des éducations physique et intellectuelle.

B. Manuels scolaires et illustrations

Dès le début de la Troisième République, les illustrations occupent une place importante dans la composition matérielle des manuels (Choppin, 1992 ; Perret-Truchot, ici même). Le soin apporté à la confection de ces manuels à destination des jeunes élèves traduit l’importance symbolique de ce type d’ouvrages. Deux remarques s’imposent ici. D’une part, les illustrations peuvent être analysées comme des représentations sociales et culturelles spécifiques d’une époque, traduisant un regard sur la société contemporaine et les éléments que l’on souhaite souligner dans l’instruction et l’éducation des élèves (Bastos et Busnello, 2004 ; Cecatto et Fernandes, 2012 ; Jacques et Ermel, 2013). D’autre part, elles traduisent aussi une prise de conscience de la spécificité enfantine des apprentissages qui requiert l’utilisation des sens (Choppin, 1992). Comme le souligne Renonciat, dès le XVI^e siècle, l’image didactique est un « support de connaissance en elle-même » reposant sur son réalisme, et elle « est un support d’apprentissage seulement dans la mesure où elle incite à l’observation du réel » (2011 :11), constituant ainsi un substitut d’un objet absent.

Legros, quant à elle, évoque les illustrations dans son étude de manuels d’arithmétique de la Troisième République : « A travers ces quelques manuels sélectionnés à des époques différentes [entre les décennies 1880 et 1930], on perçoit l’évolution typographique dans la conception des manuels. L’attractivité est travaillée et serait alors obtenue grâce à une utilisation de plus en plus systématique des illustrations qui permettent d’impliquer les enfants dans les problèmes. » (Legros, 2013 : 195). Elle fait le constat d’une faible présence d’illustrations dans certains manuels, notamment au début de la Troisième République. Les illustrations sont alors utilisées pour introduire des problèmes mathématiques, pour montrer des objets mathématiques.

C. Eléments méthodologiques

Les huit manuels retenus ont été analysés à l’aide d’indicateurs extraits des textes de Vézin (1986a) et Vézin (1986b). Deux groupes d’indicateurs ont été utilisés, portant sur les types d’illustrations présentes dans les manuels, et les différentes fonctions de ces mêmes illustrations.

II. Des savoirs mathématiques inégalement répartis

L’intention première de ce travail est de repérer les savoirs mathématiques présents dans les illustrations de quelques manuels scolaires en arithmétique et en travail manuel, ainsi que leurs fonctions. Tout d’abord, il faut souligner la difficulté de classifier les différents types d’illustrations présents dans les manuels. Si les photographies sont aisément identifiables, il est quelquefois difficile de distinguer un dessin d’un schéma ou d’un croquis (Vézin J.-F., 1986 ; Vézin L., 1986). De la même façon, il a pu être difficile d’identifier la fonction d’une illustration. Les intentions réelles des auteurs et éditeurs ne nous sont pas connues. Il faut donc noter ici un possible biais d’interprétation. De plus, les auteurs que nous avons pu consulter (Matalliotaki, 2010 ; Vézin J.-F., 1986 ; Vézin L., 1986) ne partagent pas les mêmes classifications, nous obligeant à dégager nos propres analyses des fonctions des illustrations (Perret-Truchot, 2018).

D’ores et déjà, il faut mentionner un usage varié des illustrations en arithmétique et en travaux manuels, montrant des savoirs mathématiques utilisés dans des situations différentes.

A. Les illustrations dans les manuels d’arithmétique de Leyssenne

L’analyse des illustrations en arithmétique a été menée dans les manuels que Pierre Leyssenne a publiés au début de la Troisième République, soit précisément au moment où se mettait en place l’école républicaine. Une présence importante des illustrations est d’emblée perceptible. Le tableau ci-après montre que le nombre d’illustrations va croissant au fur et à mesure du niveau des élèves.

Figure 1 : Nombre d’illustrations dans les manuels de Leyssenne en regard du nombre de pages

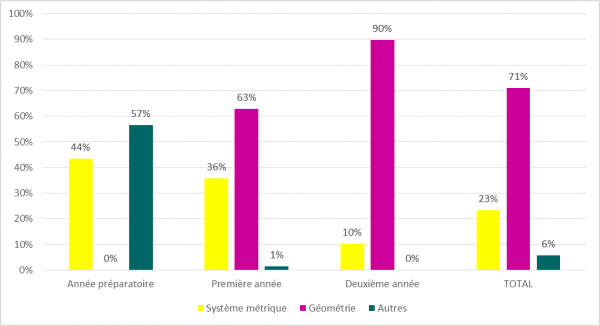
73 % des illustrations concernent des savoirs en géométrie. Même si les programmes de 1882 précisent les contenus à apprendre en géométrie en cours élémentaire (CE), l’Année préparatoire ne comprend pas de chapitre qui lui soit consacré. Les chapitres consacrés à la géométrie dans la Première année et dans la Deuxième année d’arithmétique, regroupent respectivement 63 % et 90 % des illustrations de ces ouvrages (cf. figure 2).

Figure 2 : Répartition des illustrations par champ de savoir dans les manuels de P. Leyssenne

73 % des illustrations présentées en géométrie sont des schémas, telles dans les figures n° 3 et 4, alors que les dessins ne représentent que 26 % des illustrations. Vézin (J.F., 1986) différencie le schéma et le dessin : le schéma a une valeur de généralité quand le dessin illustratif « montre ainsi un objet de la catégorie dans sa particularité » (Vézin J.F., 1986 : 71), ce qui permet de s’en faire une représentation mentale.

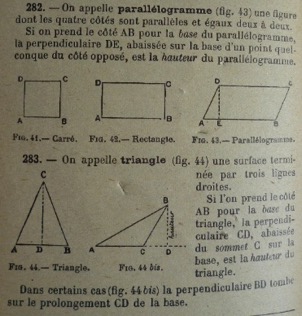
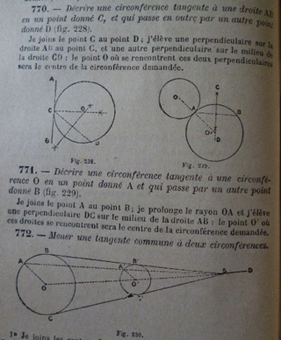
La plus forte utilisation des schémas semble ici constituer une spécificité de la géométrie qui requiert de la part des élèves des capacités d’abstraction plus importantes. Les illustrations ont alors pour fonction d’aider les élèves à se représenter les objets d’apprentissage, les notions et objets évoqués dans les énoncés, par exemple, le côté AB d’un triangle (Figure 3) dans les figures les plus simples et les plus complexes, comme la tangente commune à deux circonférences (Figure 4). L’illustration est ici une aide très précieuse pour conceptualiser le savoir mathématique et en permettre l’appropriation par l’élève. Elle permet de lever « les difficultés d’accès à la pensée abstraite » en s’appuyant sur le « besoin d’un appui sensoriel » de l’enfant (Renonciat, 2011 : 14). En géométrie, une évolution de l’utilisation des illustrations est perceptible en fonction de l’âge des élèves chez Leyssenne : plus les élèves sont âgés, plus l’auteur recourt aux schémas. Dans la Première année, les schémas représentent 61 % des illustrations de l’ouvrage, alors que dans la Deuxième année, ils représentent 82 % des illustrations du manuel.

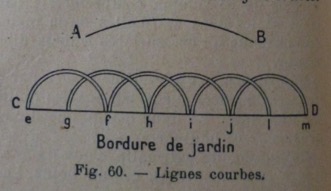
Les dessins utilisés par Leyssenne en géométrie permettent d’exemplifier les notions mathématiques travaillées. La Figure 5 associe le schéma de la ligne courbe – ligne AB – et un exemple de ce type de ligne pris dans la vie quotidienne, à savoir ici des bordures de jardin. Le schéma représente un savoir mathématique alors que le dessin associé a pour fonction de contextualiser le même savoir mathématique dans la vie quotidienne des élèves. La Figure 6 fournit un deuxième exemple – ici le cercle et la circonférence – dans une scène de la vie courante, un homme change une roue de voiture. La légende est ici tout à fait évocatrice : le dessin « donne l’idée » de l’objet mathématique.

Figure 5 : Les lignes courbes, bordure de jardin, Nouveau cours d’arithmétique, p. 144

Figure 6 : Le cercle, Nouveau cours d’arithmétique, p. 152

Leyssenne utilise également massivement les dessins dans les chapitres consacrés au système métrique. Très peu de schémas sont d’ailleurs présents dans ces chapitres. Dans cette matière, différents savoirs sont en jeu, ceux concernant les longueurs, les poids, les volumes, etc. Les dessins exposent des objets du quotidien. Les figures 7, 8 et 9 en fournissent des exemples. Les dessins à vocation illustrative insistent sur la représentation, l’imitation la plus exacte possible des objets réels – Leyssenne va jusqu’à proposer des objets « grandeur réelle » (Figure 7). Qu’il s’agisse du litre comme contenant, l’auteur en recherche les différentes occurrences dans la vie réelle (Figure 8). Le souci de précision, voire d’exhaustivité est manifeste. Dans tous ces exemples, le dessin montre un objet du quotidien des élèves qui exemplifie la notion mathématique, mais il ne s’agit pas là d’une représentation d’un savoir mathématique.

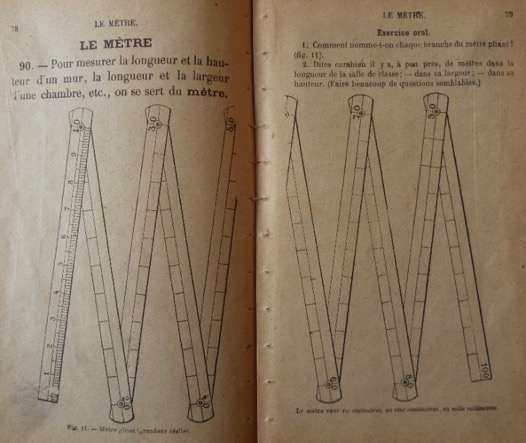
Figure 7 : Le mètre pliant (grandeur réelle), Année préparatoire, p. 78-79

En définitive, les illustrations insérées dans les manuels de Leyssenne ont deux fonctions majeures. D’une part, les schémas aident à se représenter mentalement, cognitivement les savoirs mathématiques en jeu. Ceci est particulièrement le cas en géométrie, matière qui demande de se représenter l’espace. D’autre part, les dessins ont pour fonction de resituer, de contextualiser des savoirs mathématiques en les mettant en correspondance avec des objets de la vie quotidienne des élèves. En cela, Leyssenne est parfaitement dans l’esprit des instructions du 27 juillet 1882 qui précisent : « ces connaissances sont choisies de telle sorte, que (…) elles assurent à l’enfant tout le savoir pratique dont il aura besoin dans la vie ».

B. Les illustrations en travaux manuels

Dans le corpus des quatre ouvrages analysés en travail manuel, une approche quantitative permet de faire ressortir une utilisation beaucoup plus massive des illustrations dans les manuels pour garçons (591) que dans les manuels destinés aux filles (138). Les manuels de garçons présentent ainsi quatre fois plus d’illustrations que ceux à destination des filles.

Numériquement, les dessins représentent 59 % des illustrations dans ces manuels, soit la catégorie la mieux représentée. Les schémas constituent la deuxième catégorie avec 34 % des illustrations. Les croquis, seulement présents pour les garçons représentent 5,5 % des illustrations, et les photos seules présentes pour les filles, 1,5 %. Statistiquement d’emblée, les illustrations plus réalistes tels que les dessins et les photographies sont plus présentes dans les livres à destination des filles, tandis que les illustrations présentant une plus grande part de généralité comme les schémas ou les croquis sont plus présents dans les ouvrages à destination des garçons.

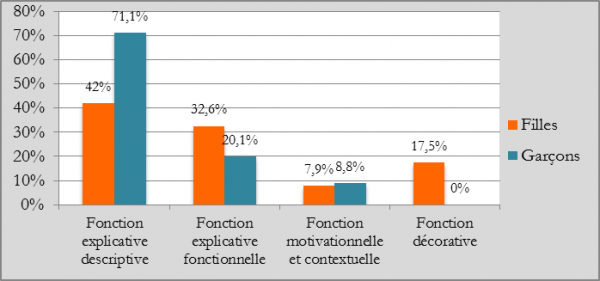
Figure 10 : Les fonctions des illustrations à destination des filles ou des garçons

Les illustrations sont majoritairement présentées avec une intention descriptive puis fonctionnelle, c’est-à-dire d’explicitation d’un processus. Ce constat corrobore la présence massive de schémas et de dessins évoquée juste avant. La fonction descriptive des illustrations est néanmoins majoritaire dans les ouvrages masculins, alors que des illustrations fonctionnelles sont un peu plus présentes pour les filles. Une analyse sexuée plus précise s’impose…

Le Cours de travail manuel de Planty, à destination des garçons, fournit un ensemble d’illustrations de travaux manuels en cours de réalisation, avec des explications textuelles quant aux différentes étapes à suivre. Cette composition du manuel offre ainsi, en s’aidant des illustrations, une procédure, des instructions à exécuter pour réaliser l’objet. Ce livre est le seul à présenter la majorité de ses illustrations en couleur, (Figure 11), exhaussant ainsi l’attractivité de l’ouvrage.

Figure 11 : Exemple de schémas proposés aux garçons, Planty, 1888, non paginé

En suivant la définition du schéma de Jean-François Vezin (1986), la Figure 11 présente une forte valeur de généralité, il ne comprend même pas de mesure. L’image de la boîte avec son couvercle propose une représentation générique : des surfaces polygonales. La même procédure pourrait être exécutée pour fabriquer une boîte de base rectangulaire, par exemple.

Les schémas présents dans ce manuel ont deux fonctions : d’une part montrer le matériel et l’organisation générale des figures à découper, et d’autre part expliquer le processus de construction de l’objet final. Les illustrations aident donc l’élève à mieux comprendre le texte, à se représenter mentalement les objets. Le composant descriptif est utilisé pour les parties du texte « parfois difficile[s] de traduire par des mots », et le composant fonctionnel quand « l’illustration permet de visualiser l’exposé d’un processus ou d’un système » (L. Vezin, 1986 : 118).

Le deuxième manuel destiné aux garçons, Les travaux manuels à l’école primaire, présente aussi des savoirs mathématiques intégrés dans des dessins, schémas et croquis. Les croquis sont des « représentations à grands traits qui montrent l’essentiel du sujet, du motif, effectués sous la forme d’esquisses, communs au monde des peintres, sculpteurs et architectes » (Encyclopédia Universalis, 2017). Le croquis de la Figure 12 présente les différentes perspectives d’un objet que les enfants doivent réaliser. Comme dans le manuel précédent, le croquis permet de visualiser les différentes étapes d’une procédure de construction d’un objet. Il fournit les perspectives et aide l’élève à mieux se représenter l’objet final dans l’espace (L. Vezin, 1986 : 118).

Figure 12 : Exemple de croquis aux garçons, Dauzat & Deramond, s.d., p. 57

La construction des objets proposée aux garçons dans les ouvrages requiert l’utilisation de nombreux outils et savoirs mathématiques. Les notions de mesure, perspective, constructions géométriques, figures planes et dans l’espace, instruments du dessin géométrique notamment sont mobilisées dans le texte et dans les illustrations.

Les deux manuels destinés aux filles ont en commun de présenter des chapitres sur les travaux de couture, la coupe et la broderie. Ce sont les seules activités manuelles proposées à ces jeunes filles de l’école primaire. Par exemple, dans La première année d’économie domestique, la majorité des images, pour la plupart des schémas, illustrent les parties consacrées à la réalisation de patrons, aux notions de coupe et de couture. Le dessin de la Figure 13 montre de manière simple la façon de marquer des morceaux sur un lé de tissu pour ensuite couper les différentes pièces de tissu nécessaires à la confection de la robe.

Figure13 : Exemple de dessin à destination des filles, Chalamet, 1893, p. 165

Le marquage des pièces de tissu permet ici d’utiliser des mesures, des connaissances géométriques. Le texte à l’appui fournit les mesures à reproduire : « La longueur de la robe sera de 45 centimètres. Mais il faut songer à l’ourlet du bas et au rentré du haut. Ajoutons 5 centimètres pour l’ourlet et un centimètre pour le rentré. Total, 51 centimètres. » (Chalamet, 1893 : 164). Les dimensions proposées semblent correspondre à la confection d’une robe de poupée, une de ces « activités enfantines de réalisations d’objets » (Lebeaume, 2015). Toutefois aucune indication n’est ajoutée concernant une possible adaptation de cette procédure pour réaliser une robe de fillette ou de femme.

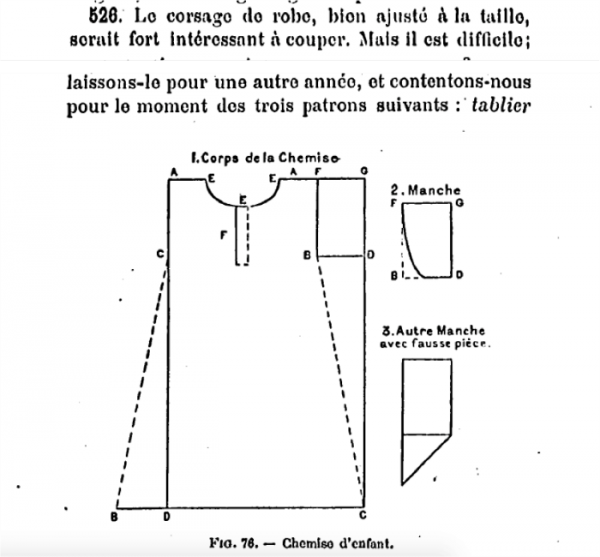
Dans les manuels destinés aux filles, les savoirs mathématiques utilisés sont peu nombreux : seules quelques notions de mesures, proportions et formes géométriques apparaissent. La Figure 14 présente ainsi les différentes pièces nécessaires à la confection d'une chemise.

Figure 14 : Exemple de schéma à destination des filles (Chalamet, 1893, p. 169-170)

Cependant ici, il n'y a pas de correspondance entre l'image et le texte concernant le processus de confection de la chemise. Des formes géométriques et des segments de figures sont présents dans le schéma, mais le code mathématique ne peut pas être déchiffré dans l’illustration, ni à l’aide du texte. Les mesures sont également absentes. Les savoirs géométriques présentés ici ne sont d’aucune utilité réelle si l’on veut suivre la procédure proposée par le manuel. Ainsi, les objectifs du travail manuel pour les filles ne sont pas de promouvoir une connaissance étayée intellectuellement des activités manuelles, mais plutôt de proposer des connaissances très sommaires des savoirs domestiques qui participent de la formation de la future femme-épouse-mère.

Le deuxième livre du corpus destinés aux filles, Cours de travaux manuels, présente les mêmes caractéristiques. Les illustrations montrent les différents types de points de couture, leur forme et leur processus de réalisation. Toutefois, ce manuel propose en sus des photographies pour illustrer le texte. Celles-ci ont plutôt pour objectif de rendre la composition plus esthétique, l’ensemble plus attractif, et aussi peut-être de motiver les jeunes filles en montrant une réalisation achevée. Par exemple, la photo présentée en Figure 15 permet de montrer aux filles le résultat final d’un travail en tricot et d’agrémenter un début de chapitre de l’ouvrage.

Figure 15 : Une photo d’un ouvrage de tricot, dans un manuel destiné aux filles, Robbe, 1905, p. 4

Ainsi les deux manuels destinés aux filles ne présentent que très peu de savoirs mathématiques. Les seules mobilisations observées du côté des filles concernent des mesures et des figures géométriques employées dans la coupe et la réalisation de vêtements. Ces illustrations sont utilisées pour aider les jeunes filles à se représenter les différentes pièces du patron à réaliser. Des figures et éléments géométriques sont montrés, mais pas nommés.

Pour conclure, et conformément au plan d'études des écoles primaires publiques de 27 juillet 1882, les travaux manuels ne présentent pas les mêmes objectifs pour les filles et pour les garçons. Leur enseignement oblige les garçons à utiliser des connaissances intellectuelles, ce qui participe à leur formation intellectuelle. Du côté des filles, l’intention est seulement de leur fournir les éléments essentiels pour devenir une bonne « femme-épouse-mère » (Lebeaume, 1995 : 135), cette finalité de l'école l’emporte sur celle d’une formation intellectuelle des filles.

Conclusion

Les analyses ont néanmoins permis d’identifier des savoirs mathématiques insérés dans des illustrations. En premier lieu, les manuels d’arithmétique proposent des illustrations qui ont pour seule fonction de montrer des savoirs mathématiques. Des galettes permettent de représenter des fractions, des collections, les figures géométriques permettent de visualiser des notions complexes. En travail manuel de la même façon, l’illustration permet de se représenter mentalement une boîte ou un couvercle de boîte à réaliser. Les illustrations permettent également de montrer des savoirs mathématiques utilisés comme outils au service d’un autre objectif. En travail manuel, ils vont servir à la réalisation d’objets. Ainsi les mesures permettent de donner des indications quant aux dimensions des objets à réaliser. En arithmétique, des savoirs mathématiques sont insérés et représentés via des objets du quotidien.

Dans les deux situations précédentes, les savoirs mathématiques sont présentés dans des illustrations qui ont pour fonction première de montrer un concept mathématique ou géométrique, ou un objet à réaliser, ou une situation/un objet du quotidien des enfants. La vocation de ces images est donc prioritairement descriptive. Les illustrations peuvent également avoir pour vocation de montrer un processus, par exemple processus de construction d’une figure géométrique, de réalisation d’un cartonnage, ou d’un point de couture. L’image propose alors la visualisation d’une procédure à suivre.

Les manuels scolaires de la Troisième République, que ce soit en arithmétique ou en travail manuel, proposent donc des illustrations variées dans leur forme et dans leur fonction. Toutefois toutes ne montrent pas des savoirs mathématiques. Beaucoup n’ont pour seule fonction que de rendre l’ouvrage plus esthétique – comme en travail manuel – ou bien de montrer des objets du quotidien, comme par exemple des pièces de monnaies ou des ouvrages de tricot.

Pendant la Troisième République, les instructions officielles permettent également de diffuser des pratiques pédagogiques plus novatrices, notamment les leçons de choses dont l’utilisation est largement préconisée. Dans ce contexte, l’illustration pourrait être envisagée comme support de départ aux apprentissages, comme première étape de la leçon ou du chapitre. Cette situation n’a jamais été observée dans les manuels analysés.

En dernier lieu, que ce soit en travail manuel ou en arithmétique, des différences sexuées sont perceptibles quant à l’utilisation des illustrations. En arithmétique, aucune femme ou fille n’est intégrée dans une illustration. En travail manuel, les illustrations sont plus réalistes pour les filles alors qu’elles demandent de plus grande capacité d’abstraction pour les garçons.