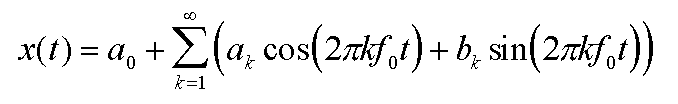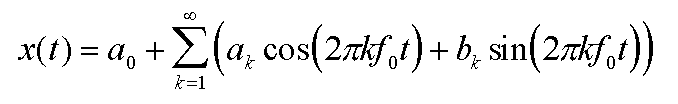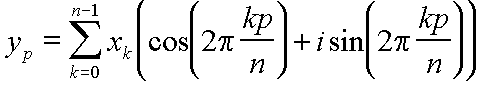|
La transformée de Fourier rapide
|
(Fast Fourier Transform, FFT)
Dernière mise à jour : 1 Mai 2003
Je remercie Don Cross d'avoir autorisé la traduction de ce document.
Le site original étant actuellement (et, je l'espère, temporairement)
indisponible, j'ai remplacé tous les liens qui le concernaient par des références
à d'autres sites où le lecteur pourra trouver des programmes de transformée de
Fourier en divers langages. En effet, seules les versions en
Pascal sont distribuées sur ce site.
Table des matières
Didacticiel sur la transformée de Fourier rapide
1. Introduction à l'audio numérique
Si les concepts de l'audio numérique vous sont familiers, vous pouvez
sauter cette section.
Le type le plus courant d'enregistrement audio numérique est
appelé modulation par impulsions codées (pulse
code modulation, PCM). C'est la technique utilisée par les disques
compacts et la plupart des fichiers WAV. Dans un système d'enregistrement
PCM, un microphone convertit les variations de pression de l'air (ondes
sonores) en variations de voltage. Ensuite, un convertisseur analogique-numérique
mesure (échantillonne) le voltage à intervalles de temps
réguliers. Par exemple, sur un disque compact, il y a exactement
44,100 échantillons par seconde. Chaque voltage est converti en
un entier de16 bits. Un CD contient deux canaux de données : un
pour l'oreille droite et un pour l'oreille gauche, afin de produire l'effet
stéréophonique. Les deux canaux sont des enregistrements
indépendants placés "côte à côte" sur
le disque compact. (En fait, les données des deux canaux alternent...
gauche, droite, gauche, droite, ... comme les pieds pendant la marche.)
Les données qui résultent d'un enregistrement PCM représentent
une fonction du temps. Les gens sont souvent surpris d'apprendre qu'une
séquence de millions d'entiers enregistrée sur un disque
compact peut reproduire la musique et la parole. Ils ont tendance à
demander "Comment un flux de nombres peut-il sonner comme un orchestre
entier ?" ; ça paraît magique, et ça l'est ! Cependant
la magie n'est pas dans l'enregistrement numérique ; elle est dans
votre oreille et votre cerveau. Pour le comprendre, imaginez que vous puissiez
placer une caméra microscopique dans votre oreille pour filmer votre
tympan au ralenti. Supposez que la caméra soit assez rapide pour
prendre une image chaque 1/44100 de seconde. Supposez aussi que les images
prises par cette caméra soient si précises que vous puissiez
discerner 65536 (64K) positions distinctes du tympan dans son mouvement
de va-et-vient en réponse aux ondes sonores incidentes. Si vous
utilisiez cette caméra hypothétique pour filmer votre tympan
pendant que votre meilleur(e) ami(e) prononce votre nom, puis que vous
preniez le film et notiez numériquement la position du tympan dans
chaque plan du film, vous auriez un enregistrement PCM. Si vous pouviez
ensuite imprimer à votre tympan un mouvement de va-et-vient en accord
avec les milliers de nombres que vous avez notés, vous entendriez
la voix de votre ami(e) prononçant votre nom exactement comme la
première fois. La nature exacte du son importe peu - votre ami(e),
une foule, une symphonie - le concept reste le même. Quand vous écoutez
plusieurs choses à la fois, les différents sons se combinent
dans vos oreilles en une unique variation de pression. Vos oreilles et
votre cerveau collaborent pour décomposer ce signal en sensations
auditives distinctes. Tout se passe littéralement dans votre tête !
2. Information fréquentielle d'une fonction du temps
Un organe de notre oreille interne appelé la cochlée
nous permet de détecter la tonalité des sons que nous entendons.
La cochlée est acoustiquement couplée au tympan par une série
de trois osselets. Elle consiste en une spirale de tissu baignant dans
un liquide et couverte de milliers de cils. Les cils de la face externe
de la spirale sont plus longs que ceux de la face interne. En fait, les
cils deviennent de plus en plus courts lorsqu'on approche du centre de
la spirale. Chaque cil est connecté à une fibre nerveuse
qui rejoint le nerf auditif en direction du cerveau. Les cils les plus
longs entrent en résonance avec les sons ayant les plus basses fréquences,
les cils les plus courts avec les plus hautes fréquences. Ainsi
la cochlée transforme les variations de pression captées
par le tympan en une information fréquentielle que le cerveau interprète
comme une tonalité et une texture. C'est ce qui nous permet de différencier
deux touches adjacentes du piano, même si elles sont jouées
avec la même intensité. La transformée de Fourier est
une technique mathématique qui réalise une tâche analogue
: décomposer une fonction du temps en un spectre de fréquences,
à la manière d'un prisme qui décompose la lumière
en un spectre de couleurs. Cette analogie n'est pas parfaite, mais elle
retient l'idée de base.
3. La transformée de Fourier en tant que concept mathématique
La transformée de Fourier est basée sur la découverte
que toute fonction périodique du temps x(t) peut être
décomposée en une somme infinie de sinus et cosinus dont
les fréquences commencent à zéro et augmentent par
multiples entiers d'une fréquence de base f0 =
1/T, où T est la période de x(t).
Ce développement se présente ainsi :
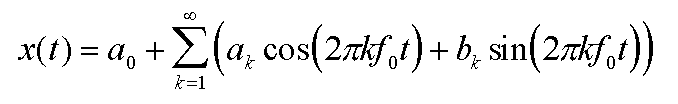 L'expression du membre de droite est appelée série de
Fourier. Le rôle de la transformée de Fourier est de trouver
toutes les valeurs ak et bk qui composent
la série, connaissant la fréquence de base et la fonction
x(t). Vous pouvez considérer le terme a0
à l'extérieur de la somme comme le coefficient du cosinus
pour k=0. Il n'y a pas de coefficient correspondant b0
pour le sinus car le sinus de zéro vaut zéro, et donc ce
coefficient n'aurait pas d'effet.
L'expression du membre de droite est appelée série de
Fourier. Le rôle de la transformée de Fourier est de trouver
toutes les valeurs ak et bk qui composent
la série, connaissant la fréquence de base et la fonction
x(t). Vous pouvez considérer le terme a0
à l'extérieur de la somme comme le coefficient du cosinus
pour k=0. Il n'y a pas de coefficient correspondant b0
pour le sinus car le sinus de zéro vaut zéro, et donc ce
coefficient n'aurait pas d'effet.
Bien sûr, aucun ordinateur réel ne peut calculer de sommes
infinies ; il nous faut donc trouver un ensemble fini de sinus et cosinus.
C'est facile à faire pour une entrée numérique échantillonnée,
si nous stipulons qu'il y ait autant de fréquences en sortie qu'il
y a de valeurs temporelles en entrée. Nous profitons aussi du fait
que tout enregistrement audio numérique a une longueur finie. Nous
pouvons prétendre que la fonction x(t) est périodique,
et que la période est égale à la longueur de l'enregistrement.
En d'autres termes, imaginons que l'enregistrement se répéte
continuellement, et appelons x(t) cette fonction. La durée
de la section répétée définit la fréquence
de base f0 dans l'équation ci-dessus. En d'autres
termes, f0 = samplingRate / N,
où N est le nombre d'échantillons dans l'enregistrement.
Par exemple, si vous utilisez un taux d'échantillonnage (samplingRate)de
44100 échantillons / seconde, et que la longueur de votre enregistrement
(N) est de 1024 échantillons, la durée représentée
par l'enregistrement est 1024 / 44100 = 0.02322 seconde, de sorte que la
fréquence de base f0 sera 1 / 0.02322 = 43.07
Hz. Si vous soumettez ces 1024 échantillons à la FFT, vous
obtiendrez les coefficients ak et bk
des sinus et cosinus pour les fréquences 43.07Hz, 2*43.07Hz, 3*43.07Hz,
etc. Pour vérifier que la transformée fonctionne correctement,
vous pourriez générer tous les sinus et cosinus correspondant
à ces fréquences, les multiplier par leur coefficients
ak et bk respectifs, tout additionner,
et vous retrouveriez votre enregistrement d'origine ! Il est un peu étrange
que tout cela fonctionne !
4. L'algorithme de la transformée de Fourier rapide
La transformée de Fourier discrète est un algorithme qui
convertit une fonction du temps à valeurs complexes échantillonnées
en une fonction à valeurs complexes de la fréquence, également
échantillonnée. La plupart du temps, nous travaillons sur
des fonctions à valeurs réelles, donc nous fixons toutes
les parties imaginaires des entrées à zéro. Si vous
voulez utiliser mon code source, voici quelques points
à connaître :
-
Vos tableaux d'entrée et de sortie doivent avoir la même taille,
que nous appellerons n.
-
La valeur de n doit être une puissance entière positive
de 2. Par exemple, un tableau de taille 1024 est permis, mais pas un de
taille 1000. La plus petite taille permise est 2. Il n'y a pas de limite
supérieure à la taille de n à part les limitations
liées à l'allocation de mémoire pour les tableaux
(entrée{réel, imaginaire}, sortie{réel, imaginaire})
et au temps d'exécution de cet algorithme en O(n*log(n)).
-
Le tableau realOut contient les coefficients des cosinus dans
la formule de Fourier.
-
Le tableau imagOut contient les coefficients des sinus dans la
formule de Fourier.
-
L'ordre des fréquences dans les tableaux de sortie (realOut
et imagOut) est un peu étrange, parce que ces fréquences
peuvent être positives aussi bien que négatives. Les deux
sont nécessaires pour des raisons mathématiques quand les
entrées ont des valeurs complexes (c'est-à-dire quand l'une
au moins des entrées a une composante imaginaire non nulle). La
plupart du temps, la FFT s'utilise sur des données réelles,
notamment dans le cas des signaux audio. La FFT, lorsqu'elle reçoit
une entrée à valeurs réelles, fournit une sortie dont
les fréquences positives et négatives sont redondantes, en
ce sens que les valeurs correspondantes sont conjuguées complexes
l'une de l'autre, ce qui signifie que leurs parties réelles sont
égales et que leurs parties imaginaires sont opposées. Si
vos entrées ont toutes des valeurs réelles, toute l'information
dont vous avez besoin se trouve dans la première moitié des
tableaux de sortie.
-
Le premier élément en sortie, realOut[0] et imagOut[0],
contient la valeur moyenne de toutes les entrées. Pour les indices
i = 1, 2, 3, ..., n/2, la valeur de la fréquence exprimée
en Hz est f = samplingRate * i / n. Les contreparties
négatives des fréquences positives en i = 1, 2, 3,
..., n/2 - 1 correspondent aux indices i' = n - i.
Voici un exemple : supposons que la fréquence d'échantillonnage
soit de 44100 Hz, et que nous utilisions des tampons de 1024 nombres complexes
pour l'entrée et la sortie. La fréquence en i = 1
serait (44100 Hz) * 1 / 1024 = 43.07 Hz. La fréquence négative
correspondante serait en i = 1024 - 1 = 1023 (soit le dernier élément
du tableau), avec une valeur de -43.07 Hz. De même, i = 17
correspondrait à une fréquence de (43.07 Hz)*17 = 732.13
Hz, tandis que i = 1024 - 17 = 1007 correspondrait à -732.13
Hz, etc.
-
L'indice n/2 est un cas particulier : il correspond à la
fréquence de Nyquist, qui est toujours égale à
la moitié de la fréquence d'échantillonnage dans un
enregistrement PCM. Par exemple, la fréquence de Nyquist d'un
CD audio vaut (44100 Hz)/2 = 22050 Hz. La fréquence de Nyquist est
importante car c'est la plus haute fréquence qu'un enregistrement
PCM peut reproduire. Le PCM ne peut rien représenter au-dessus de
cette fréquence. Si vous essayez d'échantillonner un signal
de fréquence supérieure à celle de Nyquist, il s'ensuit
une une sévère distorsion, connue sous le nom d'aliasing,
et analogue aux illusions d'optique des vieux westerns qui font que les
roues semblent tourner à l'envers. Les ingénieurs du son
savent qu'ils doivent filtrer tous les signaux analogiques au-dessus de
la fréquence de Nyquist avant de les numériser, afin d'éviter
les problèmes d'aliasing. Notez que cette limitation est
inhérente à l'enregistrement numérique lui-même,
qu'il fasse ou non l'objet de la FFT.
-
Si le signal d'entrée de la FFT est réel, le résultat
correspondant à la fréquence de Nyquist, d'indice n/2,
aura toujours une valeur réelle (ce qui signifie que sa partie imaginaire
sera nulle, ou proche de zéro du fait des erreurs d'arrondi). En
effet, d'après la formule précédente, i' =
n - n/2 = n/2, donc la fréquence de Nyquist
est égale à sa contrepartie négative. Le résultat
correspondant doit donc être égal à son conjugué
complexe, il ne peut donc s'agir que d'un nombre réel.
-
Parfois vous ne vous intéresserez qu'au module (magnitude) ou à l'argument (angle)
du résultat, pour chaque composant de fréquence.
Voici comment les calculer :
#include <math.h>
double magnitude = sqrt ( realOut[i]*realOut[i] + imagOut[i]*imagOut[i] );
double angle = atan2 ( imagOut[i], realOut[i] );
Pour faire la conversion inverse, de la magnitude et l'angle vers les parties
réelles et imaginaires, utilisez le code suivant :
#include <math.h>
double real = magnitude * cos(angle);
double imag = magnitude * sin(angle);
Pour une meilleure compréhension mathématique de la transformée
de Fourier discrète, l'équation suivante donne la relation
exacte entre l'entrée et la sortie. Dans cette équation,
xk est le kième nombre complexe
en entrée (domaine temporel), yp est le
pième nombre complexe en sortie (domaine fréquentiel),
et n = 2N est le nombre total d'échantillons.
Notez que k et p sont dans l'intervalle 0 .. n-1.
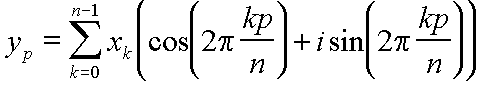 Cette formule définit la transformée de Fourier discrète,
mais pas l'algorithme FFT. En effet, cette formule requiert un nombre
d'opérations de l'ordre de n2, alors que la FFT
est de l'ordre de n*log2(n). En d'autre termes,
si vous utilisiez la formule ci-dessus, le calcul serait beaucoup plus
long qu'avec l'algorithme FFT. Cependant, si vous n'avez besoin que d'un
petit sous-ensemble du spectre de fréquences (disons deux ou trois
points), ou si le nombre de points n'est pas une puissance de 2, cette
formule combinée à quelques optimisations
trigonométriques peut être utile. Notez que c'est exactement
ce que j'ai fait pour mon code source en Turbo Pascal
dans la procédure appelée CalcFrequency.
Cette formule définit la transformée de Fourier discrète,
mais pas l'algorithme FFT. En effet, cette formule requiert un nombre
d'opérations de l'ordre de n2, alors que la FFT
est de l'ordre de n*log2(n). En d'autre termes,
si vous utilisiez la formule ci-dessus, le calcul serait beaucoup plus
long qu'avec l'algorithme FFT. Cependant, si vous n'avez besoin que d'un
petit sous-ensemble du spectre de fréquences (disons deux ou trois
points), ou si le nombre de points n'est pas une puissance de 2, cette
formule combinée à quelques optimisations
trigonométriques peut être utile. Notez que c'est exactement
ce que j'ai fait pour mon code source en Turbo Pascal
dans la procédure appelée CalcFrequency.
5. Applications de la FFT
L'algorithme FFT convient mieux à l'analyse des enregistrements
audio numériques qu'au filtrage ou à la synthèse sonore.
Elle permet par exemple d'obtenir l'équivalent logiciel d'un analyseur
de spectre, que les ingénieurs utilisent pour tracer le graphe
des fréquences contenues dans un signal électrique. Vous
pouvez utiliser la FFT pour déterminer la fréquence d'une
note dans une musique enregistrée, pour essayer d'identifier des
oiseaux ou des insectes, etc. La FFT s'utilise aussi dans des domaines
qui n'ont rien à voir avec le son, tels que le traitement d'image
(avec une version bi-dimensionnelle de la FFT). La FFT a aussi des applications
scientifiques ou statistiques, par exemple pour essayer de détecter
des fluctuations périodiques dans les prix du marché, les
populations animales, etc. La FFT s'applique aussi à l'analyse des
informations sismographiques, qui permettent de prendre des "sonogrammes"
de l'intérieur de la Terre. Même l'analyse des séquences
d'ADN utilise la transformée de Fourier !
Le principal inconvénient de la FFT dans le traitement du son
est que l'enregistrement numérique doit être divisé
en blocs de n valeurs, où n doit toujours être
une puissance entière de 2. On pourrait prendre la FFT d'un bloc,
modifier le tableau de sortie en mettant à zéro les valeurs
correspondant aux fréquences situées en dehors d'un certain
intervalle, puis calculer la transformée inverse pour retrouver
un signal temporel filtré. Quand le signal audio est décomposé
de la sorte et traité par la FFT, le résultat filtré
présente des discontinuités qui se traduisent par un "clic"
à chaque changement de bloc. Par exemple, si l'enregistrement a
un taux d'échantillonnage de 44100 Hz, et que les blocs ont une
taille n = 1024, il y aura un "clic" audible chaque1024 / (44100
Hz) = 0.0232 seconde, ce qui est extrêmement ennuyeux pour dire le
moins.
J'ai pu me débarrasser partiellement de ces discontinuités
avec la méthode suivante. Supposez que la taille du tampon est n
= 2N. A la première itération, lisez n
valeurs du signal d'entrée, calculez la FFT, modifiez la sortie
si nécessaire, calculez la transformée inverse, et conservez
les données temporelles résultantes dans un premier tampon
de sortie. Ensuite, copiez la deuxième moitié du tableau
d'entrée sur la première (rappelez-vous que n est
une puissance de 2, donc divisible par 2), et lisez n/2 nouveaux
points dans la deuxième moitié du tableau. Effectuez à
nouveau le traitement (FFT, modification, IFFT) et conservez le résultat
dans un nouveau tampon de sortie. Sur la deuxième moitié
du premier tampon de sortie, appliquez une atténuation linéaire
en multipliant chaque valeur par un coefficient variant de 1 (pour le point
d'indice n/2) à 0 (pour le point d'indice n - 1).
Sur la la première moitié du deuxième tampon de sortie,
appliquez une expansion linéaire (avec des coefficients allant de
0 à 1) et regroupez les deux moitiés pour obtenir une sortie
qui soit une transition douce entre les deux parties. Notez que les zones
entourant chaque discontinuité sont virtuellement effacées
de la sortie, bien qu'un niveau constant soit maintenu. Cette technique
marche bien lorsque le traitement ne modifie pas l'information de phase
du spectre de fréquences. Par exemple, un filtre passe-bas marchera
très bien, mais vous pourrez avoir des distorsions lors d'un décalage
de hauteur (pitch shifting).
Autres sites sur la FFT
-
Algorithmes pour le calcul scientifique.
Théorie mathématique de la FFT avec des programmes en C.
- Numerical Analysis by Jean-Pierre Moreau.
Programmes en C, Fortran, Basic et Pascal.
- Version en Visual Basic du programme de Don Cross.
-
FFTW - The "Fastest Fourier
Transform in the West" - développé au MIT par Matteo Frigo et Steven G.
Johnson. Regardez ici si vous êtes intéressé par un code source FFT portable pour
l'analyse multi-dimensionnelle, ou si vous avez un tampon dont la taille n'est pas une puissance de 2.
-
FFT for 2D
matrices in Fortran par Hon W Yau, Bhaven Avalani et Alok Choudhary.
-
Numerical
Recipes - La version online de cet ouvrage incontournable.
Le chapitre 12 présente la théorie de la FFT, et le chapitre
13 discute les applications. La consultation requiert un visualiseur Adobe
Acrobat ou PostScript.
-
La page de Numerical Recipes.
-
Amara's Wavelet Page
- Nombreux liens sur la transformée de Fourier et la transformée en ondelettes.